Published online by Cambridge University Press: 23 January 2017
A drop impacting on a solid surface must push away the intervening gas layer before making contact. This entails a large lubricating air pressure which can deform the bottom of the drop, thus entrapping a bubble under its centre. For a millimetric water drop, the viscous-dominated flow in the thin air layer counteracts the inertia of the drop liquid. For highly viscous drops the viscous stresses within the liquid also affect the interplay between the drop and the gas. Here the drop also forms a central dimple, but its outer edge is surrounded by an extended thin air film, without contacting the solid. This is in sharp contrast with impacts of lower-viscosity drops where a kink in the drop surface forms at the edge of the central disc and makes a circular contact with the solid. Larger drop viscosities make the central air dimple thinner. The thin outer air film subsequently ruptures at numerous random locations around the periphery, when it reaches below 150 nm thickness. This thickness we measure using high-speed two-colour interferometry. The wetted circular contacts expand rapidly, at orders of magnitude larger velocities than would be predicted by a capillary–viscous balance. The spreading velocity of the wetting spots is 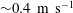 ${\sim}0.4~\text{m}~\text{s}^{-1}$ independent of the liquid viscosity. This may suggest enhanced slip of the contact line, assisted by rarefied-gas effects, or van der Waals forces in what we call extreme wetting. Myriads of micro-bubbles are captured between the local wetting spots.
${\sim}0.4~\text{m}~\text{s}^{-1}$ independent of the liquid viscosity. This may suggest enhanced slip of the contact line, assisted by rarefied-gas effects, or van der Waals forces in what we call extreme wetting. Myriads of micro-bubbles are captured between the local wetting spots.
Video of reflective interferometry taken from below an impacting drop (𝝂 = 10 cSt; Rb= 1.90 mm; V = 1.20 m/s). The video was recorded at 500 kfps and is played back at 10 fps. The horizontal extent is 0.82 mm.
Video of reflective interferometry taken from below an impacting drop (𝝂 = 1,000 cSt; Rb= 1.88 mm; V = 1.09 m/s). The video was recorded at 500 kfps and is played back at 10 fps. The horizontal extent is 1.76 mm.