Published online by Cambridge University Press: 12 December 2016
We describe a formulation of two-dimensional geometrical shock dynamics (GSD) suitable for ideal magnetohydrodynamic (MHD) fast shocks under magnetic fields of general strength and orientation. The resulting area–Mach-number–shock-angle relation is then incorporated into a numerical method using pseudospectral differentiation. The MHD-GSD model is verified by comparison with results from nonlinear finite-volume solution of the complete ideal MHD equations applied to a shock implosion flow in the presence of an oblique and spatially varying magnetic field ahead of the shock. Results from application of the MHD-GSD equations to the stability of fast MHD shocks in two dimensions are presented. It is shown that the time to formation of triple points for both perturbed MHD and gas-dynamic shocks increases as 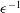 $\unicode[STIX]{x1D716}^{-1}$, where
$\unicode[STIX]{x1D716}^{-1}$, where  $\unicode[STIX]{x1D716}$ is a measure of the initial Mach-number perturbation. Symmetry breaking in the MHD case is demonstrated. In cylindrical converging geometry, in the presence of an azimuthal field produced by a line current, the MHD shock behaves in the mean as in Pullin et al. (Phys. Fluids, vol. 26, 2014, 097103), but suffers a greater relative pressure fluctuation along the shock than the gas-dynamic shock.
$\unicode[STIX]{x1D716}$ is a measure of the initial Mach-number perturbation. Symmetry breaking in the MHD case is demonstrated. In cylindrical converging geometry, in the presence of an azimuthal field produced by a line current, the MHD shock behaves in the mean as in Pullin et al. (Phys. Fluids, vol. 26, 2014, 097103), but suffers a greater relative pressure fluctuation along the shock than the gas-dynamic shock.