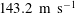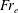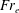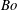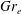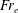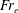1 Introduction
Gelatine has received considerable attention in the scientific community as it is an effective analogue for human tissue. For example, gelatine is used for studies on traumatic brain injury (Kang et al.
Reference Kang, Chen, Bagchi and O’Shaughnessy2017, Reference Kang, Adnan, O’Shaughnessy and Bagchi2018; Pan et al.
Reference Pan, Kiyama, Tagawa, Daily, Thomson, Hurd and Truscott2017) and fabrication of drug delivery systems (Tagawa et al.
Reference Tagawa, Oudalov, Ghalbzouri, Sun and Lohse2013; Battula, Menezes & Hosseini Reference Battula, Menezes and Hosseini2016; Moradiafrapoli & Marston Reference Moradiafrapoli and Marston2017; Kiyama et al.
Reference Kiyama, Endo, Kawamoto, Katsuta, Oida, Tanaka and Tagawa2019). However, because the properties (e.g. shear modulus
![]() $G$
) are rate-sensitive, the deformation dynamics is challenging to model.
$G$
) are rate-sensitive, the deformation dynamics is challenging to model.
A current area of research is the penetration of a solid sphere into gelatine. When a sphere falls onto gelatine, two typical events occur depending on the impact velocity. For relatively small impact velocities, the sphere does not penetrate into the gelatine (Swain et al. Reference Swain, Kieser, Shah and Kieser2014); instead, it bounces off. For higher impact velocities, a cylindrical cavity forms (Liu et al. Reference Liu, Fan, Li and Liu2012; Ryckman, Powell & Lew Reference Ryckman, Powell and Lew2012; Wen et al. Reference Wen, Xu, Wang, Chen and Batra2013; Swain et al. Reference Swain, Kieser, Shah and Kieser2014; Veysset et al. Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018). Here we find that while the cavities formed by spheres penetrating gelatine and water have some differences, they share many similarities as well. For instance, cavity shapes produced in gelatine and water (see figure 1) appear similarly shaped with both sealing near the free surface. In contrast, gelatine produces cavities having remarkably non-uniform cavity textures (see also Wen et al. Reference Wen, Xu, Wang, Chen and Batra2013).

Figure 1. Solid spheres introduce different cavity dynamics between gelatine and water with the same Froude number
![]() $Fr=u_{0}^{2}/(gR)\sim 1.0\times 10^{5}$
, where the impact speed is
$Fr=u_{0}^{2}/(gR)\sim 1.0\times 10^{5}$
, where the impact speed is
![]() $u_{0}\sim 15~\text{m}~\text{s}^{-1}$
, the gravitational acceleration is
$u_{0}\sim 15~\text{m}~\text{s}^{-1}$
, the gravitational acceleration is
![]() $g=9.81~\text{m}~\text{s}^{-2}$
and the sphere radius is
$g=9.81~\text{m}~\text{s}^{-2}$
and the sphere radius is
![]() $R=2.25$
mm. (a) A copper-coated steel sphere impacts onto a
$R=2.25$
mm. (a) A copper-coated steel sphere impacts onto a
![]() $1~\text{wt}\%$
gelatine surface and forms a conical cavity with distinct wavy surface textures. (b) In water, similar impact conditions produce a long and smooth cavity.
$1~\text{wt}\%$
gelatine surface and forms a conical cavity with distinct wavy surface textures. (b) In water, similar impact conditions produce a long and smooth cavity.
The classification of specific ‘cavity types’ can provide important information for understanding complex cavity dynamics. Cavity types in water and viscoelastic fluids have been studied by Akers & Belmonte (Reference Akers and Belmonte2006) and Aristoff & Bush (Reference Aristoff and Bush2009), respectively. In water, Aristoff & Bush (Reference Aristoff and Bush2009) classified cavities by the position of the cavity sealing event. By considering the effects of inertia, gravity and surface tension, they proposed a phase diagram of four cavity types using the Weber number
![]() $We$
and the Bond number
$We$
and the Bond number
![]() $Bo$
. More recently, Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) revealed that the boundaries for each cavity type in the
$Bo$
. More recently, Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) revealed that the boundaries for each cavity type in the
![]() $We$
–
$We$
–
![]() $Bo$
mapping shift with changes in the sphere–water wetting angle and surface roughness. In viscoelastic fluids, Akers & Belmonte (Reference Akers and Belmonte2006) reported a unique surface texture on the cavity walls (in a solution of 80 mM CPCl and 60 mM NaSal) where a phase diagram was proposed considering both sphere inertia and liquid elasticity. Although several different cavity types in gelatine have been reported (Liu et al.
Reference Liu, Fan, Li and Liu2012; Wen et al.
Reference Wen, Xu, Wang, Chen and Batra2013; Liu, Fan & Li Reference Liu, Fan and Li2014a
; Liu et al.
Reference Liu, Jia, Ma, Fan, Li and Liu2014b
; Veysset et al.
Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018), mapping the cavity regimes remains an open question.
$Bo$
mapping shift with changes in the sphere–water wetting angle and surface roughness. In viscoelastic fluids, Akers & Belmonte (Reference Akers and Belmonte2006) reported a unique surface texture on the cavity walls (in a solution of 80 mM CPCl and 60 mM NaSal) where a phase diagram was proposed considering both sphere inertia and liquid elasticity. Although several different cavity types in gelatine have been reported (Liu et al.
Reference Liu, Fan, Li and Liu2012; Wen et al.
Reference Wen, Xu, Wang, Chen and Batra2013; Liu, Fan & Li Reference Liu, Fan and Li2014a
; Liu et al.
Reference Liu, Jia, Ma, Fan, Li and Liu2014b
; Veysset et al.
Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018), mapping the cavity regimes remains an open question.
Here, we examine high-speed images of the gelatine deformation in the wake of a solid sphere impact. By varying the impact speed
![]() $u_{0}$
(
$u_{0}$
(
![]() $0.4~\text{m}~\text{s}^{-1}\leqslant u_{0}\leqslant 143.2~\text{m}~\text{s}^{-1}$
) and gelatine concentration
$0.4~\text{m}~\text{s}^{-1}\leqslant u_{0}\leqslant 143.2~\text{m}~\text{s}^{-1}$
) and gelatine concentration
![]() $C$
(
$C$
(
![]() $1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
), we show the formation of four different types of cavities similar to those observed in water. Based on our parametric study, we classify the cavity types based on their sealing position and discuss their length and dynamics. We then propose a phase diagram using two relevant non-dimensional numbers.
$1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
), we show the formation of four different types of cavities similar to those observed in water. Based on our parametric study, we classify the cavity types based on their sealing position and discuss their length and dynamics. We then propose a phase diagram using two relevant non-dimensional numbers.
2 Experimental set-up
A schematic of the experimental set-up is shown in figure 2(a). We fill an acrylic container (100 mm
![]() $\times$
100 mm
$\times$
100 mm
![]() $\times$
250 mm) partially with water or gelatine to a height of 150 mm. A copper-coated sphere (radius
$\times$
250 mm) partially with water or gelatine to a height of 150 mm. A copper-coated sphere (radius
![]() $R=2.25$
mm, density
$R=2.25$
mm, density
![]() $\unicode[STIX]{x1D70C}_{s}\sim 6800~\text{kg}~\text{m}^{-3}$
) is shot from an air rifle (Crossman 760) into the pool. A spray coating (Glaco mirror coat zero) was used to make the sphere hydrophobic and provide a single contact angle (
$\unicode[STIX]{x1D70C}_{s}\sim 6800~\text{kg}~\text{m}^{-3}$
) is shot from an air rifle (Crossman 760) into the pool. A spray coating (Glaco mirror coat zero) was used to make the sphere hydrophobic and provide a single contact angle (
![]() $141^{\circ }$
, Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). The sphere travels through the air and impacts the pool surface with a speed of
$141^{\circ }$
, Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). The sphere travels through the air and impacts the pool surface with a speed of
![]() $u_{0}$
. A high-speed colour camera (Phantom v2510) is used to record the impact event and the cavity formation up to 50 000 f.p.s. with a
$u_{0}$
. A high-speed colour camera (Phantom v2510) is used to record the impact event and the cavity formation up to 50 000 f.p.s. with a
![]() $0.2~\text{mm}~\text{pix}^{-1}$
spatial resolution. Matlab image analysis is used to capture the motion of the sphere and cavity. Measurements of the cavity dimensions at the time of pinch-off are defined by the free body diagram in figure 2(b).
$0.2~\text{mm}~\text{pix}^{-1}$
spatial resolution. Matlab image analysis is used to capture the motion of the sphere and cavity. Measurements of the cavity dimensions at the time of pinch-off are defined by the free body diagram in figure 2(b).
The water–gelatine mixture (
![]() $1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
) is prepared by boiling distilled water (approximately 0.75 L) and mixing with gelatine powder (Nowfoods, Beef Gelatin Powder) for 12 min. The concentration of gelatine is controlled based on the weight percentage of gelatine used. The solution is kept in a refrigerator overnight (22 to 26 h) and then in the laboratory at room temperature (
$1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
) is prepared by boiling distilled water (approximately 0.75 L) and mixing with gelatine powder (Nowfoods, Beef Gelatin Powder) for 12 min. The concentration of gelatine is controlled based on the weight percentage of gelatine used. The solution is kept in a refrigerator overnight (22 to 26 h) and then in the laboratory at room temperature (
![]() ${\sim}23\,^{\circ }\text{C}$
) for several hours before conducting the impact experiments. Although the bulk temperature of the gelatine and the humidity were not measured, we assume that they only cause small variations in the penetration event (Jussila Reference Jussila2004).
${\sim}23\,^{\circ }\text{C}$
) for several hours before conducting the impact experiments. Although the bulk temperature of the gelatine and the humidity were not measured, we assume that they only cause small variations in the penetration event (Jussila Reference Jussila2004).
We present the rheological properties and density of all concentrations of gelatine in table 1. All rheological tests are performed using a TA Instruments AR 2000 rheometer where the temperature of the geometry is set at
![]() $4\,^{\circ }\text{C}$
. The elastic (storage) modulus
$4\,^{\circ }\text{C}$
. The elastic (storage) modulus
![]() $G^{\prime }$
and the viscous (loss) modulus
$G^{\prime }$
and the viscous (loss) modulus
![]() $G^{\prime \prime }$
are measured using strain-sweep tests where the shear modulus, also known as the complex modulus, is calculated as
$G^{\prime \prime }$
are measured using strain-sweep tests where the shear modulus, also known as the complex modulus, is calculated as
![]() $G=\sqrt{G^{\prime 2}+G^{\prime \prime 2}}$
. Here the gelatine stiffness increases with concentration
$G=\sqrt{G^{\prime 2}+G^{\prime \prime 2}}$
. Here the gelatine stiffness increases with concentration
![]() $C$
, and
$C$
, and
![]() $G^{\prime }$
is much larger than
$G^{\prime }$
is much larger than
![]() $G^{\prime \prime }$
for all concentrations. The ratio of
$G^{\prime \prime }$
for all concentrations. The ratio of
![]() $G^{\prime }$
and
$G^{\prime }$
and
![]() $G^{\prime \prime }$
values (
$G^{\prime \prime }$
values (
![]() $\tan \unicode[STIX]{x1D6FF}$
) are presented in table 1 (see also supplementary material available at https://doi.org/10.1017/jfm.2019.696). The values are much smaller than unity, and the
$\tan \unicode[STIX]{x1D6FF}$
) are presented in table 1 (see also supplementary material available at https://doi.org/10.1017/jfm.2019.696). The values are much smaller than unity, and the
![]() $1~\text{wt}\%$
gelatine is slightly higher than the others, suggesting that the
$1~\text{wt}\%$
gelatine is slightly higher than the others, suggesting that the
![]() $1~\text{wt}\%$
gelatine will flow relatively more easily when a large deformation is applied. Note that all the rheological properties are measured under a small strain regime (limitation of our rheometer) and thus these values may not perfectly reflect the features of gelatine dynamics under severe deformation (i.e. sphere impact).
$1~\text{wt}\%$
gelatine will flow relatively more easily when a large deformation is applied. Note that all the rheological properties are measured under a small strain regime (limitation of our rheometer) and thus these values may not perfectly reflect the features of gelatine dynamics under severe deformation (i.e. sphere impact).
The relevant non-dimensional parameters include the Froude number
![]() $Fr$
, the Weber number
$Fr$
, the Weber number
![]() $We$
, the Bond number
$We$
, the Bond number
![]() $Bo$
, the elastic Froude number
$Bo$
, the elastic Froude number
![]() $\mathit{Fr}_{e}$
and the elastic Grashof number
$\mathit{Fr}_{e}$
and the elastic Grashof number
![]() $\mathit{Gr}_{e}$
. Definitions and ranges of each parameter are listed in table 2, where
$\mathit{Gr}_{e}$
. Definitions and ranges of each parameter are listed in table 2, where
![]() $\unicode[STIX]{x1D70C}$
is the density of pool medium. The measured density of water is
$\unicode[STIX]{x1D70C}$
is the density of pool medium. The measured density of water is
![]() $\unicode[STIX]{x1D70C}\sim 992~\text{kg}~\text{m}^{-3}$
(see supplementary material), the surface tension of water is
$\unicode[STIX]{x1D70C}\sim 992~\text{kg}~\text{m}^{-3}$
(see supplementary material), the surface tension of water is
![]() $\unicode[STIX]{x1D70E}=72~\text{mN}~\text{m}^{-1}$
and the gravitational acceleration is
$\unicode[STIX]{x1D70E}=72~\text{mN}~\text{m}^{-1}$
and the gravitational acceleration is
![]() $g=9.81~\text{m}~\text{s}^{-2}$
. Note that we modified the definition of the elastic Froude number and the elastic Grashof number used in Akers & Belmonte (Reference Akers and Belmonte2006), where the density difference
$g=9.81~\text{m}~\text{s}^{-2}$
. Note that we modified the definition of the elastic Froude number and the elastic Grashof number used in Akers & Belmonte (Reference Akers and Belmonte2006), where the density difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}(=\unicode[STIX]{x1D70C}_{s}-\unicode[STIX]{x1D70C})$
was adopted for both non-dimensional parameters. These numbers compare the shear modulus
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}(=\unicode[STIX]{x1D70C}_{s}-\unicode[STIX]{x1D70C})$
was adopted for both non-dimensional parameters. These numbers compare the shear modulus
![]() $G$
with the inertia and gravity (buoyancy), while the Weber number and the Bond number compare the surface tension with inertia and gravity.
$G$
with the inertia and gravity (buoyancy), while the Weber number and the Bond number compare the surface tension with inertia and gravity.

Figure 2. (a) Schematic of the experimental set-up. A copper-coated steel sphere is shot from the air rifle. A gelatine container is placed below the nozzle of the rifle. A high-speed camera films the cavity motion in the gelatine with diffuse back lighting. High-speed video is recorded and analysed on the computer. Photographs similar to figure 1 are taken with a Canon EOS 5D using a laser-sensor to trigger the camera. (b) Free body diagram. Here
![]() $R$
is the radius of the sphere. Cavity dimensions are measured at the first pinch-off of the cavity: the total cavity length
$R$
is the radius of the sphere. Cavity dimensions are measured at the first pinch-off of the cavity: the total cavity length
![]() $H$
, pinch-off depth
$H$
, pinch-off depth
![]() $H_{p}$
, maximum radius of the upper portion of the cavity
$H_{p}$
, maximum radius of the upper portion of the cavity
![]() $R_{U}$
and the maximum radius of the lower portion of the cavity
$R_{U}$
and the maximum radius of the lower portion of the cavity
![]() $R_{L}$
.
$R_{L}$
.
Table 1. Properties of the different gelatines. The elastic (storage) modulus
![]() $G^{\prime }$
, the viscous (loss) modulus
$G^{\prime }$
, the viscous (loss) modulus
![]() $G^{\prime \prime }$
, the shear (complex) modulus
$G^{\prime \prime }$
, the shear (complex) modulus
![]() $G$
, density
$G$
, density
![]() $\unicode[STIX]{x1D70C}$
and the gel fluidity represented by the angle
$\unicode[STIX]{x1D70C}$
and the gel fluidity represented by the angle
![]() $\tan \unicode[STIX]{x1D6FF}=G^{\prime \prime }/G^{\prime }$
are presented for each gelatine concentration
$\tan \unicode[STIX]{x1D6FF}=G^{\prime \prime }/G^{\prime }$
are presented for each gelatine concentration
![]() $C$
. For comparison purposes, the typical stress caused by surface tension
$C$
. For comparison purposes, the typical stress caused by surface tension
![]() $\unicode[STIX]{x1D70E}/R$
is approximately 32 Pa and the density of water was measured as
$\unicode[STIX]{x1D70E}/R$
is approximately 32 Pa and the density of water was measured as
![]() $992~\text{kg}~\text{m}^{-3}$
. More details are provided in the supplementary material.
$992~\text{kg}~\text{m}^{-3}$
. More details are provided in the supplementary material.

Table 2. Definition and range of non-dimensional parameters.

3 Observations
The most apparent difference between cavities formed in gelatine and water is the appearance of surface texture (figure 1). The surface texture varies depending on the gelatine concentration and sphere impact speed, where larger gelatine concentrations require higher impact speeds to produce the phenomenon (figure 3 c–f). Figure 3(c) reveals that the surface texture stays at the formation location where the shape of the texture becomes more apparent with the radial expansion of the cavity. The images do not reveal whether the surface texturing is plastic (permanent) or elastic; however, there is sufficient evidence that the cavity does appear to create a permanent hole in the gelatine pool (discussed later and in supplementary movie 3). While the exact cause of the surface texture is not known, we postulate it to be due to one or all of the following: crack propagation (Arakawa & Takahashi Reference Arakawa and Takahashi1991), shear-induced cavity removal similar to viscoelastic fluids (Akers & Belmonte Reference Akers and Belmonte2006) or surface-solid attachment similar to surface tension effects (Enriquez et al. Reference Enriquez, Peters, Gekle, Schmidt, Lohse and van Der Meer2012).

Figure 3. Image sequences of cavities in various media with a Froude number of
![]() $Fr\sim 4.1\times 10^{5}$
and an impact speed of
$Fr\sim 4.1\times 10^{5}$
and an impact speed of
![]() $u_{0}\sim 30~\text{m}~\text{s}^{-1}$
. (a) Surface-seal cavity in water (
$u_{0}\sim 30~\text{m}~\text{s}^{-1}$
. (a) Surface-seal cavity in water (
![]() $\unicode[STIX]{x0394}t=0.4~\text{ms}$
,
$\unicode[STIX]{x0394}t=0.4~\text{ms}$
,
![]() $We\sim 4.1\times 10^{4}$
,
$We\sim 4.1\times 10^{4}$
,
![]() $\mathit{Bo}\sim 6.8\times 10^{-1}$
), where
$\mathit{Bo}\sim 6.8\times 10^{-1}$
), where
![]() $\unicode[STIX]{x0394}t$
is the temporal image spacing (also see supplementary movie 1). (b) Surface-seal cavity in
$\unicode[STIX]{x0394}t$
is the temporal image spacing (also see supplementary movie 1). (b) Surface-seal cavity in
![]() $1~\text{wt}\%$
gelatine (
$1~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=0.4~\text{ms}$
,
$\unicode[STIX]{x0394}t=0.4~\text{ms}$
,
![]() $\mathit{Fr}_{e}\sim 1.9\times 10^{4}$
,
$\mathit{Fr}_{e}\sim 1.9\times 10^{4}$
,
![]() $\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
, supplementary movie 2). (c) Shallow-seal cavity in
$\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
, supplementary movie 2). (c) Shallow-seal cavity in
![]() $2~\text{wt}\%$
gelatine (
$2~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=1.2~\text{ms}$
,
$\unicode[STIX]{x0394}t=1.2~\text{ms}$
,
![]() $\mathit{Fr}_{e}\sim 4.0\times 10^{3}$
,
$\mathit{Fr}_{e}\sim 4.0\times 10^{3}$
,
![]() $\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
). Surface texture is obvious on the cavity wall (supplementary movie 3). (d) Shallow-seal cavity in
$\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
). Surface texture is obvious on the cavity wall (supplementary movie 3). (d) Shallow-seal cavity in
![]() $3~\text{wt}\%$
gelatine (
$3~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=0.56~\text{ms}$
,
$\unicode[STIX]{x0394}t=0.56~\text{ms}$
,
![]() $\mathit{Fr}_{e}\sim 1.4\times 10^{3}$
,
$\mathit{Fr}_{e}\sim 1.4\times 10^{3}$
,
![]() $\mathit{Gr}_{e}\sim 2.3\times 10^{-2}$
, supplementary movie 4). (e) shallow-seal in
$\mathit{Gr}_{e}\sim 2.3\times 10^{-2}$
, supplementary movie 4). (e) shallow-seal in
![]() $5~\text{wt}\%$
gelatine (
$5~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=0.24~\text{ms}$
,
$\unicode[STIX]{x0394}t=0.24~\text{ms}$
,
![]() $\mathit{Fr}_{e}\sim 1.9\times 10^{2}$
,
$\mathit{Fr}_{e}\sim 1.9\times 10^{2}$
,
![]() $\mathit{Gr}_{e}\sim 4.1\times 10^{-3}$
, supplementary movie 5). (f) Quasi-seal cavity in
$\mathit{Gr}_{e}\sim 4.1\times 10^{-3}$
, supplementary movie 5). (f) Quasi-seal cavity in
![]() $10~\text{wt}\%$
gelatine (
$10~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=0.16~\text{ms}$
,
$\unicode[STIX]{x0394}t=0.16~\text{ms}$
,
![]() $\mathit{Fr}_{e}\sim 5.9\times 10^{1}$
,
$\mathit{Fr}_{e}\sim 5.9\times 10^{1}$
,
![]() $\mathit{Gr}_{e}\sim 1.3\times 10^{-3}$
, supplementary movie 6).
$\mathit{Gr}_{e}\sim 1.3\times 10^{-3}$
, supplementary movie 6).
We find the cavity shape to be highly dependent on the gelatine concentration. The evolution of cavities in various media is first studied keeping the impact velocity constant (
![]() $u_{0}\sim 30~\text{m}~\text{s}^{-1}$
). Similar to the events observed in water (figure 3
a, supplementary movie 1), sphere impact into a
$u_{0}\sim 30~\text{m}~\text{s}^{-1}$
). Similar to the events observed in water (figure 3
a, supplementary movie 1), sphere impact into a
![]() $1~\text{wt}\%$
gelatine pool creates a splash sheet from the air–gelatine interface, which then results in the formation of a surface seal (figure 3
b, supplementary movie 2). The sphere propagation speed and cavity size are noted to be similar in both the water and
$1~\text{wt}\%$
gelatine pool creates a splash sheet from the air–gelatine interface, which then results in the formation of a surface seal (figure 3
b, supplementary movie 2). The sphere propagation speed and cavity size are noted to be similar in both the water and
![]() $1~\text{wt}\%$
gelatine. However, in a more concentrated gel, the cavity elongates and collapses just below the air–gelatine interface, which results in a distinct shallow seal (figure 3
c–e, supplementary movies 3–5). This event occurs on a much larger time scale (
$1~\text{wt}\%$
gelatine. However, in a more concentrated gel, the cavity elongates and collapses just below the air–gelatine interface, which results in a distinct shallow seal (figure 3
c–e, supplementary movies 3–5). This event occurs on a much larger time scale (
![]() ${\sim}6$
ms) in comparison to the surface-seal event (
${\sim}6$
ms) in comparison to the surface-seal event (
![]() ${\sim}2$
ms, figure 3
a,b). The maximum radius of the cavity
${\sim}2$
ms, figure 3
a,b). The maximum radius of the cavity
![]() $R_{L}$
decreases as
$R_{L}$
decreases as
![]() $C$
increases, such that
$C$
increases, such that
![]() $R_{L}$
becomes comparable to the sphere radius
$R_{L}$
becomes comparable to the sphere radius
![]() $R$
in
$R$
in
![]() $5~\text{wt}\%$
gelatine and less than the sphere radius
$5~\text{wt}\%$
gelatine and less than the sphere radius
![]() $R$
in the
$R$
in the
![]() $10~\text{wt}\%$
gelatine. The surface texture of the cavity walls is only visible in weak gelatine,
$10~\text{wt}\%$
gelatine. The surface texture of the cavity walls is only visible in weak gelatine,
![]() $C\leqslant 3~\text{wt}\%$
(figure 3
c–d), while a different pinch-off is noted in the
$C\leqslant 3~\text{wt}\%$
(figure 3
c–d), while a different pinch-off is noted in the
![]() $10~\text{wt}\%$
gelatine having a pinch-off depth greater than
$10~\text{wt}\%$
gelatine having a pinch-off depth greater than
![]() $0.5H$
(figure 3
f, supplementary movie 6). In addition, a necked region right above the pinch-off location (Anderson, LaCosse & Pankow Reference Anderson, LaCosse and Pankow2016) is also noted in figure 3(c–e). Akers & Belmonte (Reference Akers and Belmonte2006) found that similar necked regions occurred approximately one diameter below the surface and discussed the effects of elasticity and surface tension on the onset. In our experiment, the position of these necks for shallow-seal cases is approximately one or two sphere diameters, which is consistent with the literature. Note, the cavities herein accompanied by the dome-over event are classified as surface-seal (e.g. figure 3
b). Otherwise, cavities where the pinch-off below the air–gelatine interface occurs before the dome-over event are classified as shallow-seal (e.g. figure 3
c), even when the overall cavity shape including the opening angle of the cavity is quite similar to that for the surface seal.
$0.5H$
(figure 3
f, supplementary movie 6). In addition, a necked region right above the pinch-off location (Anderson, LaCosse & Pankow Reference Anderson, LaCosse and Pankow2016) is also noted in figure 3(c–e). Akers & Belmonte (Reference Akers and Belmonte2006) found that similar necked regions occurred approximately one diameter below the surface and discussed the effects of elasticity and surface tension on the onset. In our experiment, the position of these necks for shallow-seal cases is approximately one or two sphere diameters, which is consistent with the literature. Note, the cavities herein accompanied by the dome-over event are classified as surface-seal (e.g. figure 3
b). Otherwise, cavities where the pinch-off below the air–gelatine interface occurs before the dome-over event are classified as shallow-seal (e.g. figure 3
c), even when the overall cavity shape including the opening angle of the cavity is quite similar to that for the surface seal.
Figure 4 shows the effect of impact velocity on cavity formation in 2 wt% gelatine at different
![]() $u_{0}$
values. In figure 4(a), the sphere does not penetrate the gelatine but, rather, rebounds (supplementary movie 7). Sphere rebound in a similar manner has also been reported in water-entry experiments (Lee & Kim Reference Lee and Kim2008; Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). In such cases, the inertia of the sphere must exceed the surface tension in order to create a cavity, whereas in gelatine the inertia must overcome the elasticity. In figure 4(b), an increase in the impact speed
$u_{0}$
values. In figure 4(a), the sphere does not penetrate the gelatine but, rather, rebounds (supplementary movie 7). Sphere rebound in a similar manner has also been reported in water-entry experiments (Lee & Kim Reference Lee and Kim2008; Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). In such cases, the inertia of the sphere must exceed the surface tension in order to create a cavity, whereas in gelatine the inertia must overcome the elasticity. In figure 4(b), an increase in the impact speed
![]() $u_{0}$
leads to the formation of a cavity. Further increase in
$u_{0}$
leads to the formation of a cavity. Further increase in
![]() $u_{0}$
introduces the dome-over event and the cavity detachment from the air–gelatine interface (i.e. surface seal, figure 4
c, supplementary movie 8).
$u_{0}$
introduces the dome-over event and the cavity detachment from the air–gelatine interface (i.e. surface seal, figure 4
c, supplementary movie 8).

Figure 4. Image sequences of cavities in
![]() $2~\text{wt}\%$
gelatine (
$2~\text{wt}\%$
gelatine (
![]() $\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
) formed by spheres with different impact velocities. (a) Rebound (
$\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
) formed by spheres with different impact velocities. (a) Rebound (
![]() $u_{0}\sim 3~\text{m}~\text{s}^{-1}$
,
$u_{0}\sim 3~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 1.8\times 10^{1}$
,
$\mathit{Fr}_{e}\sim 1.8\times 10^{1}$
,
![]() $\unicode[STIX]{x0394}t=8.0$
ms, supplementary movie 7). (b) Shallow-seal cavity (
$\unicode[STIX]{x0394}t=8.0$
ms, supplementary movie 7). (b) Shallow-seal cavity (
![]() $u_{0}\sim 30~\text{m}~\text{s}^{-1}$
,
$u_{0}\sim 30~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 4.0\times 10^{4}$
,
$\mathit{Fr}_{e}\sim 4.0\times 10^{4}$
,
![]() $\unicode[STIX]{x0394}t=1.2$
ms), which is the reproduced version of figure 3(c). (c) Surface-seal cavity (
$\unicode[STIX]{x0394}t=1.2$
ms), which is the reproduced version of figure 3(c). (c) Surface-seal cavity (
![]() $u_{0}\sim 70~\text{m}~\text{s}^{-1}$
,
$u_{0}\sim 70~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 1.5\times 10^{4}$
,
$\mathit{Fr}_{e}\sim 1.5\times 10^{4}$
,
![]() $\unicode[STIX]{x0394}t=0.32$
ms, supplementary movie 8).
$\unicode[STIX]{x0394}t=0.32$
ms, supplementary movie 8).
Similar to water-entry experiments, four different cavity types are observed for impacts with gelatine pools as shown in figure 5. A time series of the impact in gelatine is presented in figure 5(a–d) with the overall shape of the gelatine cavity types at their pinch-off moment (i.e. last frame outlined in various colours). Water-entry cases at the moment of pinch-off are placed next to the last frame of the gelatine cases for comparison purposes, which shows that the two cavity types are quite similar with the exception of the presence of the surface texture and the exact location of the necked region. Digital image extraction of the gelatine and water cases are compared in figure 5(e) to emphasize the similarities between the two cases and, again, reveal that cavity size, surface texture and location of the necked regions are slightly different, but overall can be classified similarly.
More notable differences between gelatine and water-entry cases emerge after the pinch-off events. These are captured in figure 6 showing the (a) surface-seal regime in water, (b) surface-seal regime in
![]() $1~\text{wt}\%$
gelatine and (c) shallow-seal regime in
$1~\text{wt}\%$
gelatine and (c) shallow-seal regime in
![]() $3~\text{wt}\%$
gelatine pools. The two surface-seal regimes (a,b) exhibit similar behaviours where the first pinch-off occurs near frame 2 and the secondary closure (deep-seal) appears similar in depth, time and shape (frame 3). However, there are two remarkable differences. One is the height of the vertical jet above the surface (i.e. the so-called Worthington jet) from frame 4 to frame 7 where the gelatine jet has a significantly smaller height, due to elasticity. Note that, although the overall volume of the surface dome-over cavity of the
$3~\text{wt}\%$
gelatine pools. The two surface-seal regimes (a,b) exhibit similar behaviours where the first pinch-off occurs near frame 2 and the secondary closure (deep-seal) appears similar in depth, time and shape (frame 3). However, there are two remarkable differences. One is the height of the vertical jet above the surface (i.e. the so-called Worthington jet) from frame 4 to frame 7 where the gelatine jet has a significantly smaller height, due to elasticity. Note that, although the overall volume of the surface dome-over cavity of the
![]() $C=2~\text{wt}\%$
gelatine (figure 4
c) is larger than the water case (figure 3
a) and
$C=2~\text{wt}\%$
gelatine (figure 4
c) is larger than the water case (figure 3
a) and
![]() $1~\text{wt}\%$
case (figure 3
b), the accompanying vertical jet has a smaller height. This suggests that the water-like behaviour of the gelatine is suppressed as the gelatine concentration increases. The other is the existence and persistence of bubbles along the path of the cavity a long time after impact. As shown in the far-right panel of figure 6(b) (grey outlined image), the bubbles created by the sphere impact in the gelatine can be trapped for several minutes after cavity closure due to fluid viscoelasticity, while those in the water float upward immediately (not shown). In the shallow-seal case (c), the pinch-off occurs between frames 2 and 3 with the sphere decelerating up to frame 5. The air inside the cavity seems to collapse from the bottom, rising upward except for a small bubble attached to the sphere. The sphere actually moves upward between frames 6 and 8, likely due to elastic recovery (Akers & Belmonte Reference Akers and Belmonte2006; Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015). An image taken a few minutes after the impact (figure 6
c, grey outlined image) shows a narrow hole (or crack) remaining inside the gelatine along the line of sphere trajectory as proof of its plastic deformation.
$1~\text{wt}\%$
case (figure 3
b), the accompanying vertical jet has a smaller height. This suggests that the water-like behaviour of the gelatine is suppressed as the gelatine concentration increases. The other is the existence and persistence of bubbles along the path of the cavity a long time after impact. As shown in the far-right panel of figure 6(b) (grey outlined image), the bubbles created by the sphere impact in the gelatine can be trapped for several minutes after cavity closure due to fluid viscoelasticity, while those in the water float upward immediately (not shown). In the shallow-seal case (c), the pinch-off occurs between frames 2 and 3 with the sphere decelerating up to frame 5. The air inside the cavity seems to collapse from the bottom, rising upward except for a small bubble attached to the sphere. The sphere actually moves upward between frames 6 and 8, likely due to elastic recovery (Akers & Belmonte Reference Akers and Belmonte2006; Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015). An image taken a few minutes after the impact (figure 6
c, grey outlined image) shows a narrow hole (or crack) remaining inside the gelatine along the line of sphere trajectory as proof of its plastic deformation.

Figure 5. The evolution of cavity formation in gelatine for (a)
![]() $C=2~\text{wt}\%$
,
$C=2~\text{wt}\%$
,
![]() $u_{0}=3.4~\text{m}~\text{s}^{-1}$
,
$u_{0}=3.4~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 2.8\times 10^{1}$
,
$\mathit{Fr}_{e}\sim 2.8\times 10^{1}$
,
![]() $\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
,
$\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
,
![]() $\unicode[STIX]{x0394}t=1.8~\text{ms}$
. (b)
$\unicode[STIX]{x0394}t=1.8~\text{ms}$
. (b)
![]() $C=2~\text{wt}\%$
,
$C=2~\text{wt}\%$
,
![]() $u_{0}=14.4~\text{m}~\text{s}^{-1}$
,
$u_{0}=14.4~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 5.2\times 10^{2}$
,
$\mathit{Fr}_{e}\sim 5.2\times 10^{2}$
,
![]() $\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
,
$\mathit{Gr}_{e}\sim 5.5\times 10^{-2}$
,
![]() $\unicode[STIX]{x0394}t=2.0~\text{ms}$
. (c)
$\unicode[STIX]{x0394}t=2.0~\text{ms}$
. (c)
![]() $C=1~\text{wt}\%$
,
$C=1~\text{wt}\%$
,
![]() $u_{0}=2.6~\text{m}~\text{s}^{-1}$
,
$u_{0}=2.6~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 1.0\times 10^{2},\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
,
$\mathit{Fr}_{e}\sim 1.0\times 10^{2},\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
,
![]() $\unicode[STIX]{x0394}t=4.2~\text{ms}$
. (d)
$\unicode[STIX]{x0394}t=4.2~\text{ms}$
. (d)
![]() $C=1~\text{wt}\%$
,
$C=1~\text{wt}\%$
,
![]() $u_{0}=34.2~\text{m}~\text{s}^{-1}$
,
$u_{0}=34.2~\text{m}~\text{s}^{-1}$
,
![]() $\mathit{Fr}_{e}\sim 1.8\times 10^{4},\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
,
$\mathit{Fr}_{e}\sim 1.8\times 10^{4},\mathit{Gr}_{e}\sim 3.3\times 10^{-1}$
,
![]() $\unicode[STIX]{x0394}t=1.0~\text{ms}$
, in comparison with water for quasi-seal (red), shallow-seal (grey), deep-seal (blue) and surface-seal (green) cavity types. The corresponding cavity shape profiles are determined using an edge detection routine and plotted side-by-side in (e) for comparison purposes.
$\unicode[STIX]{x0394}t=1.0~\text{ms}$
, in comparison with water for quasi-seal (red), shallow-seal (grey), deep-seal (blue) and surface-seal (green) cavity types. The corresponding cavity shape profiles are determined using an edge detection routine and plotted side-by-side in (e) for comparison purposes.

Figure 6. Cavity shape after closure. (a) Surface-seal cavity in water (
![]() $\unicode[STIX]{x0394}t=2$
ms, reproduced from figure 3
a). (b) Surface-seal cavity in
$\unicode[STIX]{x0394}t=2$
ms, reproduced from figure 3
a). (b) Surface-seal cavity in
![]() $1~\text{wt}\%$
gelatine (
$1~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=2$
ms, reproduced from figure 3
b). (c) Shallow-seal cavity in
$\unicode[STIX]{x0394}t=2$
ms, reproduced from figure 3
b). (c) Shallow-seal cavity in
![]() $3~\text{wt}\%$
gelatine (
$3~\text{wt}\%$
gelatine (
![]() $\unicode[STIX]{x0394}t=2~\text{ms}$
, reproduced from figure 3
d). The last image on the right with a grey outline in panels (b) and (c) is minutes after impact (captured separately) where there are air pockets left open in the wake of the cavity. In (c) the sphere has risen slightly as the cavity closes, likely due to the elastic recovery of gelatine and the now zero inertia of the sphere (supplementary movie 9).
$\unicode[STIX]{x0394}t=2~\text{ms}$
, reproduced from figure 3
d). The last image on the right with a grey outline in panels (b) and (c) is minutes after impact (captured separately) where there are air pockets left open in the wake of the cavity. In (c) the sphere has risen slightly as the cavity closes, likely due to the elastic recovery of gelatine and the now zero inertia of the sphere (supplementary movie 9).
An important aspect of this study is that all four cavity types categorized in figure 5 can be produced by particular combinations of
![]() $C$
and
$C$
and
![]() $u_{0}$
. Thus, all five impact phenomena including rebound can be mapped into a phase diagram by considering the ratio of inertia and gelatine elasticity. In this paper, we use the elastic Froude number
$u_{0}$
. Thus, all five impact phenomena including rebound can be mapped into a phase diagram by considering the ratio of inertia and gelatine elasticity. In this paper, we use the elastic Froude number
![]() $\mathit{Fr}_{e}$
as a measure of competition between
$\mathit{Fr}_{e}$
as a measure of competition between
![]() $C$
and
$C$
and
![]() $u_{0}$
. Although this paper mainly compares cavity dynamics in gelatine with that in water, it is important to point out that the elastic Froude number
$u_{0}$
. Although this paper mainly compares cavity dynamics in gelatine with that in water, it is important to point out that the elastic Froude number
![]() $\mathit{Fr}_{e}$
could also be interpreted as a function of the shear-wave-based Mach number
$\mathit{Fr}_{e}$
could also be interpreted as a function of the shear-wave-based Mach number
![]() $Ma=u_{0}/c_{s}$
, where
$Ma=u_{0}/c_{s}$
, where
![]() $c_{s}$
is the speed of the shear wave in gelatine estimated as
$c_{s}$
is the speed of the shear wave in gelatine estimated as
![]() $c_{s}\sim \sqrt{G/\unicode[STIX]{x1D70C}}$
. Based on the definition of
$c_{s}\sim \sqrt{G/\unicode[STIX]{x1D70C}}$
. Based on the definition of
![]() $\mathit{Fr}_{e}$
and
$\mathit{Fr}_{e}$
and
![]() $Ma$
, one finds
$Ma$
, one finds
![]() $\mathit{Fr}_{e}=Ma^{2}$
, indicating that the elastic Froude number
$\mathit{Fr}_{e}=Ma^{2}$
, indicating that the elastic Froude number
![]() $\mathit{Fr}_{e}$
is not only the ratio of sphere inertia to gelatine elasticity but also the competition between the speed of cavity formation (or surface creation) and the shear wave propagation in the gelatine. Note that the speed of the longitudinal wave in gelatine, which is supposed to be close to that of the compression wave in water, is still much greater than the sphere speed, suggesting that cavity dynamics in gelatine is affected by the shear wave (Rapet, Tagawa & Ohl Reference Rapet, Tagawa and Ohl2019), where the contribution of the longitudinal wave to cavity dynamics in gelatine is supposed to be comparable to that of the compression wave in water.
$\mathit{Fr}_{e}$
is not only the ratio of sphere inertia to gelatine elasticity but also the competition between the speed of cavity formation (or surface creation) and the shear wave propagation in the gelatine. Note that the speed of the longitudinal wave in gelatine, which is supposed to be close to that of the compression wave in water, is still much greater than the sphere speed, suggesting that cavity dynamics in gelatine is affected by the shear wave (Rapet, Tagawa & Ohl Reference Rapet, Tagawa and Ohl2019), where the contribution of the longitudinal wave to cavity dynamics in gelatine is supposed to be comparable to that of the compression wave in water.
4 Discussion
Investigating the cavity length
![]() $H$
at cavity pinch-off, figure 7(a) shows a relation between the normalized cavity length
$H$
at cavity pinch-off, figure 7(a) shows a relation between the normalized cavity length
![]() $H/(2R)$
versus the elastic Froude number
$H/(2R)$
versus the elastic Froude number
![]() $\mathit{Fr}_{e}$
. The cavity length
$\mathit{Fr}_{e}$
. The cavity length
![]() $H$
for the quasi-seal, shallow seal and deep seal is measured when the cavity experiences pinch-off below the free surface (
$H$
for the quasi-seal, shallow seal and deep seal is measured when the cavity experiences pinch-off below the free surface (
![]() $t=\unicode[STIX]{x1D70F}$
). For surface-seal cases, the cavity length
$t=\unicode[STIX]{x1D70F}$
). For surface-seal cases, the cavity length
![]() $H$
is measured when the cavity seals at the free surface (
$H$
is measured when the cavity seals at the free surface (
![]() $t=t_{c}$
). We use the elastic Froude number
$t=t_{c}$
). We use the elastic Froude number
![]() $\mathit{Fr}_{e}$
to classify the cavity types in different gelatine concentrations (
$\mathit{Fr}_{e}$
to classify the cavity types in different gelatine concentrations (
![]() $1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
) into four main regimes, which are highlighted using different shapes. Rebound is noted for smaller
$1~\text{wt}\%\leqslant C\leqslant 10~\text{wt}\%$
) into four main regimes, which are highlighted using different shapes. Rebound is noted for smaller
![]() $\mathit{Fr}_{e}$
but once
$\mathit{Fr}_{e}$
but once
![]() $\mathit{Fr}_{e}$
exceeds a threshold of
$\mathit{Fr}_{e}$
exceeds a threshold of
![]() $\mathit{Fr}_{e}\sim O(10)$
, the sphere creates a quasi-seal or deep-seal cavity, shallow-seal cavities in the yellow region (
$\mathit{Fr}_{e}\sim O(10)$
, the sphere creates a quasi-seal or deep-seal cavity, shallow-seal cavities in the yellow region (
![]() $4\times 10^{1}\leqslant \mathit{Fr}_{e}\leqslant 6\times 10^{3}$
) and surface-seal cavities in the blue region (
$4\times 10^{1}\leqslant \mathit{Fr}_{e}\leqslant 6\times 10^{3}$
) and surface-seal cavities in the blue region (
![]() $\mathit{Fr}_{e}\geqslant 6\times 10^{3}$
). We note that the 1 wt% gelatine acts more like water than an elastic solid. The nearly flat response of
$\mathit{Fr}_{e}\geqslant 6\times 10^{3}$
). We note that the 1 wt% gelatine acts more like water than an elastic solid. The nearly flat response of
![]() $H/(2R)$
to
$H/(2R)$
to
![]() $\mathit{Fr}_{e}$
(yellow markers) and behaviour like the Worthington jet of figure 3 make it likely that there is a
$\mathit{Fr}_{e}$
(yellow markers) and behaviour like the Worthington jet of figure 3 make it likely that there is a
![]() $\tan \unicode[STIX]{x1D6FF}$
(table 1) threshold that delineates between water-like and elastic-like cavity shapes and sizes.
$\tan \unicode[STIX]{x1D6FF}$
(table 1) threshold that delineates between water-like and elastic-like cavity shapes and sizes.

Figure 7. (a) Normalized cavity length
![]() $H/(2R)$
versus elastic Froude number
$H/(2R)$
versus elastic Froude number
![]() $\mathit{Fr}_{e}$
. Solid line indicates the half-power law
$\mathit{Fr}_{e}$
. Solid line indicates the half-power law
![]() $H/(2R)\propto \sqrt{\mathit{Fr }_{e}}$
. Coloured areas highlight shallow-seal (yellow region) and surface-seal (blue region) cavities. (b) Normalized time of surface-seal
$H/(2R)\propto \sqrt{\mathit{Fr }_{e}}$
. Coloured areas highlight shallow-seal (yellow region) and surface-seal (blue region) cavities. (b) Normalized time of surface-seal
![]() $t_{c}/\sqrt{R/g}$
for both gelatine (coloured markers) and water (white markers) versus the Froude number
$t_{c}/\sqrt{R/g}$
for both gelatine (coloured markers) and water (white markers) versus the Froude number
![]() $Fr(=u_{0}^{2}/(gR))$
. The inset shows the normalized cavity length
$Fr(=u_{0}^{2}/(gR))$
. The inset shows the normalized cavity length
![]() $H/(2R)$
versus
$H/(2R)$
versus
![]() $u_{0}t_{c}/(2R)$
. Dashed line indicates
$u_{0}t_{c}/(2R)$
. Dashed line indicates
![]() $H/(2R)=0.71u_{0}t_{c}/(2R)$
.
$H/(2R)=0.71u_{0}t_{c}/(2R)$
.
One may estimate the transition from rebound to quasi-seal by considering the balance of contact pressure
![]() $p$
at the sphere impact and shear modulus
$p$
at the sphere impact and shear modulus
![]() $G$
. One may assume
$G$
. One may assume
![]() $p\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}u_{0}^{2}$
for simplicity purposes, which results in the application of a constant
$p\sim \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}u_{0}^{2}$
for simplicity purposes, which results in the application of a constant
![]() $\mathit{Fr}_{e}$
for cavity formation, consistent with the experimental data presented in figure 7 and those by Swain et al. (Reference Swain, Kieser, Shah and Kieser2014). However, the above oversimplistic estimation (i.e.
$\mathit{Fr}_{e}$
for cavity formation, consistent with the experimental data presented in figure 7 and those by Swain et al. (Reference Swain, Kieser, Shah and Kieser2014). However, the above oversimplistic estimation (i.e.
![]() $G<p$
for the penetration) underpredicts the condition for cavity formation by a decade. It is worth noting that we can predict very different thresholds from the data presented in the literature. For example, a constant
$G<p$
for the penetration) underpredicts the condition for cavity formation by a decade. It is worth noting that we can predict very different thresholds from the data presented in the literature. For example, a constant
![]() $\mathit{Fr}_{e}\sim 0.1$
is estimated for the ordnance gelatine (Swain et al.
Reference Swain, Kieser, Shah and Kieser2014). On the other hand, estimates for the synthetic polymer gel (Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015) are found to be
$\mathit{Fr}_{e}\sim 0.1$
is estimated for the ordnance gelatine (Swain et al.
Reference Swain, Kieser, Shah and Kieser2014). On the other hand, estimates for the synthetic polymer gel (Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015) are found to be
![]() $7.4\times 10^{1}\lesssim \mathit{Fr}_{e}\lesssim 1.3\times 10^{2}$
. The discrepancy between our data in figure 7 and Swain et al. (Reference Swain, Kieser, Shah and Kieser2014) and Mrozek et al. (Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015) indicates that the condition for cavity formation is not satisfactorily explained by
$7.4\times 10^{1}\lesssim \mathit{Fr}_{e}\lesssim 1.3\times 10^{2}$
. The discrepancy between our data in figure 7 and Swain et al. (Reference Swain, Kieser, Shah and Kieser2014) and Mrozek et al. (Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015) indicates that the condition for cavity formation is not satisfactorily explained by
![]() $\mathit{Fr}_{e}$
values. Modelling the threshold for cavity formation, possibly as a function of mechanical properties of the gel such as
$\mathit{Fr}_{e}$
values. Modelling the threshold for cavity formation, possibly as a function of mechanical properties of the gel such as
![]() $G$
values, is to be addressed in future work. In this study, the sphere rebound threshold marked by
$G$
values, is to be addressed in future work. In this study, the sphere rebound threshold marked by
![]() $\mathit{Fr}_{e}\sim O$
(10) is equivalent to
$\mathit{Fr}_{e}\sim O$
(10) is equivalent to
![]() $Ma\sim O(1)$
. This might indicate that the speed of the sphere impact is greater than that of the shear wave propagation in the gelatine when the cavity forms.
$Ma\sim O(1)$
. This might indicate that the speed of the sphere impact is greater than that of the shear wave propagation in the gelatine when the cavity forms.
In shallow-seal cases, a scaling law of the form
![]() $H\propto (u_{0}-u_{th})/\sqrt{G}$
(Swain et al.
Reference Swain, Kieser, Shah and Kieser2014; Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015), where
$H\propto (u_{0}-u_{th})/\sqrt{G}$
(Swain et al.
Reference Swain, Kieser, Shah and Kieser2014; Mrozek et al.
Reference Mrozek, Leighliter, Gold, Beringer, Yu, VanLandingham, Moy, Foster and Lenhart2015), where
![]() $u_{th}$
is the minimum sphere speed required to form the cavity, might be applicable for describing the cavity length
$u_{th}$
is the minimum sphere speed required to form the cavity, might be applicable for describing the cavity length
![]() $H$
. The relation
$H$
. The relation
![]() $H/(2R)\propto \sqrt{\mathit{Fr }_{e}}$
is thus expected, which indeed follows the data (solid line in figure 7
a). This shows the shallow-seal data and the proposed relation to be in good agreement, suggesting the elastic Froude number
$H/(2R)\propto \sqrt{\mathit{Fr }_{e}}$
is thus expected, which indeed follows the data (solid line in figure 7
a). This shows the shallow-seal data and the proposed relation to be in good agreement, suggesting the elastic Froude number
![]() $\mathit{Fr}_{e}$
is a good indicator for describing the length of the shallow-seal cavities.
$\mathit{Fr}_{e}$
is a good indicator for describing the length of the shallow-seal cavities.
In the surface-seal regime, the scaling based on the elastic Froude number
![]() $\mathit{Fr}_{e}$
no longer holds; rather, the cavity length (
$\mathit{Fr}_{e}$
no longer holds; rather, the cavity length (
![]() $H/(2R)$
) drops as
$H/(2R)$
) drops as
![]() $\mathit{Fr}_{e}$
increases. Our surface-seal data (figure 7
b) indicates that
$\mathit{Fr}_{e}$
increases. Our surface-seal data (figure 7
b) indicates that
![]() $H$
can be predicted as
$H$
can be predicted as
![]() $H=\unicode[STIX]{x1D6FC}u_{0}t_{c}$
(see inset), which assumes a constant sphere propagation speed, regardless of
$H=\unicode[STIX]{x1D6FC}u_{0}t_{c}$
(see inset), which assumes a constant sphere propagation speed, regardless of
![]() $G$
values. Here
$G$
values. Here
![]() $\unicode[STIX]{x1D6FC}=0.71\pm 0.01$
is the fitting parameter and
$\unicode[STIX]{x1D6FC}=0.71\pm 0.01$
is the fitting parameter and
![]() $t_{c}$
is the time of surface-seal. This suggests that
$t_{c}$
is the time of surface-seal. This suggests that
![]() $t_{c}$
is also insensitive to
$t_{c}$
is also insensitive to
![]() $G$
(see also figure 7
b), implying that the dynamics of surface-seal cavities is independent of
$G$
(see also figure 7
b), implying that the dynamics of surface-seal cavities is independent of
![]() $G$
for the experimental conditions investigated herein. Note that another formulation of the non-dimensional time of surface-seal
$G$
for the experimental conditions investigated herein. Note that another formulation of the non-dimensional time of surface-seal
![]() $t_{c}u_{0}/R$
shows
$t_{c}u_{0}/R$
shows
![]() $Fr$
dependency within
$Fr$
dependency within
![]() $24\leqslant t_{c}u_{0}/R\leqslant 90$
while Marston, Vakarelski & Thoroddsen (Reference Marston, Vakarelski and Thoroddsen2012) reported a constant value (
$24\leqslant t_{c}u_{0}/R\leqslant 90$
while Marston, Vakarelski & Thoroddsen (Reference Marston, Vakarelski and Thoroddsen2012) reported a constant value (
![]() $t_{c}u_{0}/R\approx 11.5$
) at lower
$t_{c}u_{0}/R\approx 11.5$
) at lower
![]() $Fr$
conditions (
$Fr$
conditions (
![]() $200\leqslant Fr\leqslant 1000$
). Aristoff & Bush (Reference Aristoff and Bush2009) suggested that the time of surface-seal
$200\leqslant Fr\leqslant 1000$
). Aristoff & Bush (Reference Aristoff and Bush2009) suggested that the time of surface-seal
![]() $t_{c}u_{0}/R$
can increase as the Weber number associated with the splash curtain dynamics increases. We also measure the pinch-off time of deep-seal
$t_{c}u_{0}/R$
can increase as the Weber number associated with the splash curtain dynamics increases. We also measure the pinch-off time of deep-seal
![]() $\unicode[STIX]{x1D70F}$
after the surface seal. Several empirical relations are reported for deep-seal cavities in water as
$\unicode[STIX]{x1D70F}$
after the surface seal. Several empirical relations are reported for deep-seal cavities in water as
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FD}\sqrt{R/g}$
, where
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FD}\sqrt{R/g}$
, where
![]() $\unicode[STIX]{x1D6FD}=2.285$
for a disk (Glasheen & McMahon Reference Glasheen and McMahon1996), and
$\unicode[STIX]{x1D6FD}=2.285$
for a disk (Glasheen & McMahon Reference Glasheen and McMahon1996), and
![]() $\unicode[STIX]{x1D6FD}=1.726$
(Truscott & Techet Reference Truscott and Techet2009),
$\unicode[STIX]{x1D6FD}=1.726$
(Truscott & Techet Reference Truscott and Techet2009),
![]() $\unicode[STIX]{x1D6FD}=1.74$
(Gilbarg & Anderson Reference Gilbarg and Anderson1948),
$\unicode[STIX]{x1D6FD}=1.74$
(Gilbarg & Anderson Reference Gilbarg and Anderson1948),
![]() $\unicode[STIX]{x1D6FD}=2.06$
(Duclaux et al.
Reference Duclaux, Caillé, Duez, Ybert, Bocquet and Clanet2007) or
$\unicode[STIX]{x1D6FD}=2.06$
(Duclaux et al.
Reference Duclaux, Caillé, Duez, Ybert, Bocquet and Clanet2007) or
![]() $\unicode[STIX]{x1D6FD}=2.09$
(Marston et al.
Reference Marston, Vakarelski and Thoroddsen2012) for spheres. A significant deviation from these, however, was reported by Mansoor et al. (Reference Mansoor, Marston, Vakarelski and Thoroddsen2014) for surface-seal events in an extended
$\unicode[STIX]{x1D6FD}=2.09$
(Marston et al.
Reference Marston, Vakarelski and Thoroddsen2012) for spheres. A significant deviation from these, however, was reported by Mansoor et al. (Reference Mansoor, Marston, Vakarelski and Thoroddsen2014) for surface-seal events in an extended
![]() $Fr$
regime where the pinch-off time
$Fr$
regime where the pinch-off time
![]() $\unicode[STIX]{x1D70F}$
decreased significantly as
$\unicode[STIX]{x1D70F}$
decreased significantly as
![]() $Fr$
increased. Measuring the time of surface-seal cases for gelatine impacts in this work produces a much smaller empirical value of
$Fr$
increased. Measuring the time of surface-seal cases for gelatine impacts in this work produces a much smaller empirical value of
![]() $\unicode[STIX]{x1D6FD}=0.28\pm 0.03$
found as being less sensitive to
$\unicode[STIX]{x1D6FD}=0.28\pm 0.03$
found as being less sensitive to
![]() $G$
values for the high
$G$
values for the high
![]() $Fr$
cases studied herein. Thus, it is suggested that the pinch-off time
$Fr$
cases studied herein. Thus, it is suggested that the pinch-off time
![]() $\unicode[STIX]{x1D70F}$
as well as the surface-seal time
$\unicode[STIX]{x1D70F}$
as well as the surface-seal time
![]() $t_{c}$
in the high
$t_{c}$
in the high
![]() $Fr$
limit are remarkably different from those in lower
$Fr$
limit are remarkably different from those in lower
![]() $Fr$
values (
$Fr$
values (
![]() $Fr<1000$
). This is possibly due to a stronger reduction in cavity pressure with higher sphere penetration speeds. While the required resolution for studying splash curtain dynamics (e.g. the splash sheet thickness) is beyond the scope of this study, the short-lived nature of these events in extremely high Froude number conditions could be another possible explanation and grounds for future studies.
$Fr<1000$
). This is possibly due to a stronger reduction in cavity pressure with higher sphere penetration speeds. While the required resolution for studying splash curtain dynamics (e.g. the splash sheet thickness) is beyond the scope of this study, the short-lived nature of these events in extremely high Froude number conditions could be another possible explanation and grounds for future studies.
A phase diagram in the non-dimensional parameter space (
![]() $\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
) is shown in figure 8(a) and a
$\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
) is shown in figure 8(a) and a
![]() $We$
–
$We$
–
![]() $Bo$
plot for water is shown for comparison purposes in figure 8(b). Our water-entry observations are in good agreement with Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) considering our sphere–water wetting angle is 141
$Bo$
plot for water is shown for comparison purposes in figure 8(b). Our water-entry observations are in good agreement with Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) considering our sphere–water wetting angle is 141
![]() $^{\circ }$
. The relationship between
$^{\circ }$
. The relationship between
![]() $We$
–
$We$
–
![]() $Bo$
and
$Bo$
and
![]() $\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
here is important as the prior indicates the comparison of sphere inertia and gravity using surface tension (
$\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
here is important as the prior indicates the comparison of sphere inertia and gravity using surface tension (
![]() $\unicode[STIX]{x1D70E}/R$
) while the latter conveys the same information using
$\unicode[STIX]{x1D70E}/R$
) while the latter conveys the same information using
![]() $G$
in both
$G$
in both
![]() $\mathit{Fr}_{e}$
and
$\mathit{Fr}_{e}$
and
![]() $\mathit{Gr}_{e}$
(see table 2). In addition to
$\mathit{Gr}_{e}$
(see table 2). In addition to
![]() $\mathit{Fr}_{e}$
being a good indicator in classifying cavity types, Akers & Belmonte (Reference Akers and Belmonte2006) have shown the transition of cavities to be dependent on
$\mathit{Fr}_{e}$
being a good indicator in classifying cavity types, Akers & Belmonte (Reference Akers and Belmonte2006) have shown the transition of cavities to be dependent on
![]() $\mathit{Gr}_{e}$
as well. Well-defined regimes for different cavities are therefore shown in an
$\mathit{Gr}_{e}$
as well. Well-defined regimes for different cavities are therefore shown in an
![]() $\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
plane (see figure 8) where increasing sphere inertia moves through different cavity types: rebound, quasi-, deep-, shallow- and surface-seal.
$\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
plane (see figure 8) where increasing sphere inertia moves through different cavity types: rebound, quasi-, deep-, shallow- and surface-seal.
There are three main points worth discussing in figure 8: (i) no rebound is observed in water, (ii) a deep seal does not appear to occur in gelatine when
![]() $\mathit{Gr}_{e}\ll$
1 and (iii) a shallow seal occurs between the deep and surface seal in gelatine for increasing
$\mathit{Gr}_{e}\ll$
1 and (iii) a shallow seal occurs between the deep and surface seal in gelatine for increasing
![]() $\mathit{Fr}_{e}$
. In (i), the onset of rebound was not observed in water-entry experiments herein, possibly because of the small contribution of surface tension compared to inertia and gravity. Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) observed rebound in water-entry experiments only when
$\mathit{Fr}_{e}$
. In (i), the onset of rebound was not observed in water-entry experiments herein, possibly because of the small contribution of surface tension compared to inertia and gravity. Speirs et al. (Reference Speirs, Mansoor, Fluid and Truscott2019) observed rebound in water-entry experiments only when
![]() $We<0.5$
and
$We<0.5$
and
![]() $Bo<0.1$
, which are not within range of current experiments. In (ii), at the lowest concentrations of gelatine (largest
$Bo<0.1$
, which are not within range of current experiments. In (ii), at the lowest concentrations of gelatine (largest
![]() $\mathit{Gr}_{e}$
) deep-seal and surface-seal events occur. Yet, at the higher gelatine concentrations, deep-seal and surface-seal events are suppressed. Aristoff & Bush (Reference Aristoff and Bush2009) suggested that the deep-seal regime in water does not exist for
$\mathit{Gr}_{e}$
) deep-seal and surface-seal events occur. Yet, at the higher gelatine concentrations, deep-seal and surface-seal events are suppressed. Aristoff & Bush (Reference Aristoff and Bush2009) suggested that the deep-seal regime in water does not exist for
![]() $Bo\ll 1$
as hydrostatic pressure, being the driving force for deep-seal events, is dominated by surface tension effects. Similarly, for
$Bo\ll 1$
as hydrostatic pressure, being the driving force for deep-seal events, is dominated by surface tension effects. Similarly, for
![]() $\mathit{Gr}_{e}\ll 1$
, the influence of gravity is small compared to gelatine elasticity, resulting in the suppression of deep-seal events therein. While the pinch-off time
$\mathit{Gr}_{e}\ll 1$
, the influence of gravity is small compared to gelatine elasticity, resulting in the suppression of deep-seal events therein. While the pinch-off time
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FD}\sqrt{R/g}$
, where
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FD}\sqrt{R/g}$
, where
![]() $\unicode[STIX]{x1D6FD}=1.89$
obtained here for water-entry experiments agrees well with previously reported values (
$\unicode[STIX]{x1D6FD}=1.89$
obtained here for water-entry experiments agrees well with previously reported values (
![]() $\unicode[STIX]{x1D6FD}=1.726$
, Truscott & Techet Reference Truscott and Techet2009;
$\unicode[STIX]{x1D6FD}=1.726$
, Truscott & Techet Reference Truscott and Techet2009;
![]() $\unicode[STIX]{x1D6FD}=2.09$
, Marston et al.
Reference Marston, Vakarelski and Thoroddsen2012), a value of
$\unicode[STIX]{x1D6FD}=2.09$
, Marston et al.
Reference Marston, Vakarelski and Thoroddsen2012), a value of
![]() $\unicode[STIX]{x1D6FD}=1.42$
obtained in 1 wt% gelatine is slightly smaller in comparison but expected. In (iii), as
$\unicode[STIX]{x1D6FD}=1.42$
obtained in 1 wt% gelatine is slightly smaller in comparison but expected. In (iii), as
![]() $We$
increases in water-entry cases, deep-seal events are noted to occur between shallow and surface seals. However, a corresponding increase in
$We$
increases in water-entry cases, deep-seal events are noted to occur between shallow and surface seals. However, a corresponding increase in
![]() $\mathit{Fr}_{e}$
for gelatine cases results in a deep seal occurring before shallow and surface seals. This is possibly due to the manner in which we classify surface and shallow seals. In our classification a surface dome-over event is a prerequisite for surface seals, which is likely to be suppressed by elasticity in gelatine impact cases (see figures 3 and 4
b,c). Maintaining the same classification criteria in both water and gelatine impact cases, cavities in the latter medium can experience suppressed surface dome-over events and hence the discrepancy observed in figure 8.
$\mathit{Fr}_{e}$
for gelatine cases results in a deep seal occurring before shallow and surface seals. This is possibly due to the manner in which we classify surface and shallow seals. In our classification a surface dome-over event is a prerequisite for surface seals, which is likely to be suppressed by elasticity in gelatine impact cases (see figures 3 and 4
b,c). Maintaining the same classification criteria in both water and gelatine impact cases, cavities in the latter medium can experience suppressed surface dome-over events and hence the discrepancy observed in figure 8.

Figure 8. (a) Phase diagram for cavity types in an
![]() $\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
plane. The shapes correspond to the cavity types. The colours indicate the concentration of gelatine as shown in figure 7. (b) The four different cavities observed in water are presented by white markers in the
$\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
plane. The shapes correspond to the cavity types. The colours indicate the concentration of gelatine as shown in figure 7. (b) The four different cavities observed in water are presented by white markers in the
![]() $We$
–
$We$
–
![]() $Bo$
plane.
$Bo$
plane.
Although the well-known classification of cavities based on the sealing position in water-entry experiments (Aristoff & Bush Reference Aristoff and Bush2009) could also be used for categorizing cavities formed in gelatine, they cannot capture all the cavity features perfectly. While the pinch-off location
![]() $H_{p}$
remains constant for different
$H_{p}$
remains constant for different
![]() $\mathit{Fr}_{e}$
conditions (see figure 3
c,d), the overall shape of the cavity, which is not only the cavity length
$\mathit{Fr}_{e}$
conditions (see figure 3
c,d), the overall shape of the cavity, which is not only the cavity length
![]() $H$
but also the maximum radius of the lower cavity
$H$
but also the maximum radius of the lower cavity
![]() $R_{L}$
, is dependent on
$R_{L}$
, is dependent on
![]() $\mathit{Fr}_{e}$
values. Thus, in order to understand the cavity features in gelatine more comprehensively, we focus on the overall cavity shape in figure 5(e) and figure 9. Figure 9(a) presents the normalized pinch-off location
$\mathit{Fr}_{e}$
values. Thus, in order to understand the cavity features in gelatine more comprehensively, we focus on the overall cavity shape in figure 5(e) and figure 9. Figure 9(a) presents the normalized pinch-off location
![]() $H_{p}/H$
where the well-known quasi-seal and deep-seal cavities are categorized by
$H_{p}/H$
where the well-known quasi-seal and deep-seal cavities are categorized by
![]() $H_{p}/H>0.5$
and
$H_{p}/H>0.5$
and
![]() $H_{p}/H\sim 0.5$
, respectively. For the shallow-seal cases,
$H_{p}/H\sim 0.5$
, respectively. For the shallow-seal cases,
![]() $H_{p}/H$
decreases as
$H_{p}/H$
decreases as
![]() $\mathit{Fr}_{e}$
increases because the cavity length
$\mathit{Fr}_{e}$
increases because the cavity length
![]() $H$
increases while
$H$
increases while
![]() $H_{p}$
remains relatively constant (figure 3). Higher
$H_{p}$
remains relatively constant (figure 3). Higher
![]() $\mathit{Fr}_{e}$
introduces surface-seal cases, where
$\mathit{Fr}_{e}$
introduces surface-seal cases, where
![]() $H_{p}/H=0$
. Note that
$H_{p}/H=0$
. Note that
![]() $H_{p}$
for surface-seal cases is measured when the splash crown seals at the free surface occurs (
$H_{p}$
for surface-seal cases is measured when the splash crown seals at the free surface occurs (
![]() $t=t_{c}$
). Here we also compare the non-dimensional pinch-off location
$t=t_{c}$
). Here we also compare the non-dimensional pinch-off location
![]() $H_{p}/R$
for shallow-seal cases of both water and gelatine in order to confirm that the pinch-off location
$H_{p}/R$
for shallow-seal cases of both water and gelatine in order to confirm that the pinch-off location
![]() $H_{p}$
is independent of the sphere impact speed. Aristoff & Bush (Reference Aristoff and Bush2009) derived a constant
$H_{p}$
is independent of the sphere impact speed. Aristoff & Bush (Reference Aristoff and Bush2009) derived a constant
![]() $H_{p}/R$
for a fixed contact angle and confirmed experimentally that the measured value was slightly correlated with the sphere impact speed up to
$H_{p}/R$
for a fixed contact angle and confirmed experimentally that the measured value was slightly correlated with the sphere impact speed up to
![]() $H_{p}/R<5$
. Our water-entry data (
$H_{p}/R<5$
. Our water-entry data (
![]() $H_{p}/R<2.7$
) agrees fairly well with their assessment. Similarly, our gelatine data shows the relatively constant pinch-off location
$H_{p}/R<2.7$
) agrees fairly well with their assessment. Similarly, our gelatine data shows the relatively constant pinch-off location
![]() $H_{p}/R$
(see inset of figure 9
a), where the mean value and the standard deviations are
$H_{p}/R$
(see inset of figure 9
a), where the mean value and the standard deviations are
![]() $H_{p}/R=3.38\pm 0.66$
. The maximum radius of the lower cavity
$H_{p}/R=3.38\pm 0.66$
. The maximum radius of the lower cavity
![]() $R_{L}/R$
increases as
$R_{L}/R$
increases as
![]() $\mathit{Fr}_{e}$
increases (figure 9
b). As discussed in figure 7(b), the cavity dynamics in gelatine for surface-seal events is quite similar to that in water, and is insensitive to
$\mathit{Fr}_{e}$
increases (figure 9
b). As discussed in figure 7(b), the cavity dynamics in gelatine for surface-seal events is quite similar to that in water, and is insensitive to
![]() $G$
values. Thus, any clear relation between
$G$
values. Thus, any clear relation between
![]() $R_{L}/R$
and
$R_{L}/R$
and
![]() $\mathit{Fr}_{e}$
is not observed for surface-seal in figure 9(b).
$\mathit{Fr}_{e}$
is not observed for surface-seal in figure 9(b).

Figure 9. The overall pinch-off and shape characteristics for all cavity types. The colour and shape indicate gelatine elasticity and cavity types as in figure 7. (a) Normalized pinch-off height
![]() $H_{p}/H$
versus elastic Froude number
$H_{p}/H$
versus elastic Froude number
![]() $\mathit{Fr}_{e}$
. Solid horizontal line indicates
$\mathit{Fr}_{e}$
. Solid horizontal line indicates
![]() $H_{p}/H=0.5$
. The inset shows the normalized pinch-off height
$H_{p}/H=0.5$
. The inset shows the normalized pinch-off height
![]() $H_{p}/R$
for shallow-seals as a function of the elastic Froude number
$H_{p}/R$
for shallow-seals as a function of the elastic Froude number
![]() $\mathit{Fr}_{e}$
. (b) The normalized maximum cavity radius
$\mathit{Fr}_{e}$
. (b) The normalized maximum cavity radius
![]() $R_{L}/R$
versus elastic Froude number
$R_{L}/R$
versus elastic Froude number
![]() $\mathit{Fr}_{e}$
. Solid horizontal line indicates
$\mathit{Fr}_{e}$
. Solid horizontal line indicates
![]() $R_{L}/R=1.0$
.
$R_{L}/R=1.0$
.
While the dynamics of surface-seal cavities has not been explored in past literature with excessive detail, the fluidic behaviour that is reported is quite similar to our findings. Veysset et al. (Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018) showed that the impact of a copper microparticle at
![]() $435~\text{m}~\text{s}^{-1}$
can cause surface dome-over at the surface of a protein hydrogel. Their maximum radius
$435~\text{m}~\text{s}^{-1}$
can cause surface dome-over at the surface of a protein hydrogel. Their maximum radius
![]() $R_{L}/R$
is found to be
$R_{L}/R$
is found to be
![]() $R_{L}/R\approx 5$
, which is comparable to that obtained from our surface-seal data. We estimate the elastic Froude number
$R_{L}/R\approx 5$
, which is comparable to that obtained from our surface-seal data. We estimate the elastic Froude number
![]() $\mathit{Fr}_{e}(=\unicode[STIX]{x1D70C}u_{0}^{2}/G)$
for Veysset case as
$\mathit{Fr}_{e}(=\unicode[STIX]{x1D70C}u_{0}^{2}/G)$
for Veysset case as
![]() $\mathit{Fr}_{e}\sim 4.7\times 10^{4}$
based on the rheological data for the protein gel as (
$\mathit{Fr}_{e}\sim 4.7\times 10^{4}$
based on the rheological data for the protein gel as (
![]() $G\sim G^{\prime }\sim 4.0\times 10^{3}$
Pa, Olsen, Kornfield & Tirrell Reference Olsen, Kornfield and Tirrell2010). While this is consistent with
$G\sim G^{\prime }\sim 4.0\times 10^{3}$
Pa, Olsen, Kornfield & Tirrell Reference Olsen, Kornfield and Tirrell2010). While this is consistent with
![]() $\mathit{Fr}_{e}$
values for the surface-seal regime in figure 8, the elastic Grashoff number
$\mathit{Fr}_{e}$
values for the surface-seal regime in figure 8, the elastic Grashoff number
![]() $\mathit{Gr}_{e}$
is not within range. Note that Veysset et al. (Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018) showed that surface dome-over does not occur when a lighter particle (silica sphere,
$\mathit{Gr}_{e}$
is not within range. Note that Veysset et al. (Reference Veysset, Kooi, Maznev, Tang, Mijailovic, Yang, Geiser, Van Vliet, Olsen and Nelson2018) showed that surface dome-over does not occur when a lighter particle (silica sphere,
![]() $\unicode[STIX]{x1D70C}_{s}\sim 1850~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}_{s}\sim 1850~\text{kg}~\text{m}^{-3}$
,
![]() $R\sim 3.7~\unicode[STIX]{x03BC}\text{m}$
) impacts the same gel at a faster velocity (
$R\sim 3.7~\unicode[STIX]{x03BC}\text{m}$
) impacts the same gel at a faster velocity (
![]() ${\sim}530~\text{m}~\text{s}^{-1}$
). Further studies are hence warranted investigating the dome-over phenomenon in viscoelastic fluids in more detail.
${\sim}530~\text{m}~\text{s}^{-1}$
). Further studies are hence warranted investigating the dome-over phenomenon in viscoelastic fluids in more detail.
5 Conclusion
This study investigates the dynamics of cavity formation when a sphere impacts onto a deep gelatine pool. The cavities were filmed using high-speed imaging and generally found to be affected by both impact velocity
![]() $u_{0}$
and gelatine elasticity
$u_{0}$
and gelatine elasticity
![]() $G$
significantly. The uniqueness of gelatine cavities in terms of shape and structure, including the formation of streaks on the cavity wall, were also outlined in comparison with those obtained in water. To understand the complex cavity dynamics in gelatine, we classify ‘cavity types’ in a non-dimensional
$G$
significantly. The uniqueness of gelatine cavities in terms of shape and structure, including the formation of streaks on the cavity wall, were also outlined in comparison with those obtained in water. To understand the complex cavity dynamics in gelatine, we classify ‘cavity types’ in a non-dimensional
![]() $\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
space analogous to the
$\mathit{Fr}_{e}{-}\mathit{Gr}_{e}$
space analogous to the
![]() $We$
–
$We$
–
![]() $Bo$
classification in water-entry cavities (Aristoff & Bush Reference Aristoff and Bush2009; Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). The normalized cavity length
$Bo$
classification in water-entry cavities (Aristoff & Bush Reference Aristoff and Bush2009; Speirs et al.
Reference Speirs, Mansoor, Fluid and Truscott2019). The normalized cavity length
![]() $H/(2R)$
is an important parameter which can be scaled by the elastic Froude number
$H/(2R)$
is an important parameter which can be scaled by the elastic Froude number
![]() $\mathit{Fr}_{e}$
, especially in shallow-seal cases. In addition, while the normalized pinch-off depths
$\mathit{Fr}_{e}$
, especially in shallow-seal cases. In addition, while the normalized pinch-off depths
![]() $H_{p}/H$
ratios decrease, the maximum radius of the lower cavity
$H_{p}/H$
ratios decrease, the maximum radius of the lower cavity
![]() $R_{L}/R$
increases with increasing
$R_{L}/R$
increases with increasing
![]() $\mathit{Fr}_{e}$
. The only exception occurs for surface-seal events (in the latter case) which are found to exhibit cavity dynamics insensitive to the shear modulus
$\mathit{Fr}_{e}$
. The only exception occurs for surface-seal events (in the latter case) which are found to exhibit cavity dynamics insensitive to the shear modulus
![]() $G$
and somewhat similar to that observed in water.
$G$
and somewhat similar to that observed in water.
Acknowledgements
This work is partially supported by the funding from Tokyo University of Agriculture and Technology, Institute of Global Innovation Research in Tokyo University of Agriculture and Technology and JSPS KAKENHI (grant nos 16J08521 and 17H01246). M.M.M., N.B.S. and T.T.T. acknowledge funding from the Office of Naval Research, Navy Undersea Research Program (grant no. N00014-18-1-2334), monitored by Ms M. Medeiros. The authors gratefully thank Professor S. Martini for the use of her rheometer and for her technical assistance.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.696.