Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T06:47:00.653Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid–structure interaction-induced oscillation of flexible structures in laminar and turbulent flows

Published online by Cambridge University Press:  09 January 2013

Jorge Pereira Gomes  and
H. Lienhart
Jorge Pereira Gomes*
Affiliation:
Institute of Fluid Mechanics and Erlangen Graduate School in Advanced Optical Technologies, University of Erlangen-Nuremberg, Cauerstrasse 4, D-91058 Erlangen, Germany
H. Lienhart
Affiliation:
Institute of Fluid Mechanics and Erlangen Graduate School in Advanced Optical Technologies, University of Erlangen-Nuremberg, Cauerstrasse 4, D-91058 Erlangen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Self-excitation of the motion of a structure has become a prominent aspect of engineering projects over recent years as designers are using materials at their limits, causing structures to become progressively lighter, more flexible and, therefore, prone to vibrate. 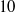Stimulated by the increasing interest in fluid–structure interaction (FSI) problems, this study investigated the instability and consequent FSI-induced self-excited oscillation of flexible structures in uniform flows at Reynolds numbers between $10$ and 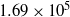$1. 69\times 1{0}^{5} $. The investigations were performed in both water and a highly viscous syrup (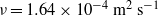$\nu = 1. 64\times 1{0}^{- 4} ~{\mathrm{m} }^{2} ~{\mathrm{s} }^{- 1} $) and considered three structures of different geometries. The results were conclusive in showing that the motion of the structure was characterized by a sequence of oscillation modes as a function of the characteristics of the structure and flow properties. In addition, it was possible to identify the self-excitation mechanisms as being of the instability-induced excitation (IIE) or movement-induced excitation (MIE) types. IIE was observed to be the most dominant mechanism of excitation at lower velocities and it was defined by a direct relation between the flow fluctuation and natural frequencies of the structure. For that reason, IIE was strongly determined by the geometry of the front body of the structure. At higher velocities, the amplitudes of the flow disturbances generated by the structure movement increased and excitations of the MIE type became predominant for all structures. The MIE mechanism was found to be weakly influenced by the shape of the structure but very sensitive to its dynamic characteristics and to the properties of the fluid, especially the Reynolds number.

JFM classification

Aerodynamics: Aerodynamics Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 537 - 572
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fey, C., Konig, M. & Eckelmann, H. 1998 A new Strouhal–Reynolds-number relationship for the circular cylinder in the range $47\lt \mathit{Re}\lt 2\times 1{0}^{5} $. Phys. Fluids 10 (7), 1547–1549.CrossRefGoogle Scholar
Gomes, J. P. & Lienhart, H. 2010a Experimental benchmark: self-excited fluid–structure interaction test cases. In Fluid Structure Interaction II (ed. Bungartz, H. J., Mehl, M. & Schäfer, M.), Lecture Notes in Computational Science and Engineering, Vol. 73, pp. 383–411. Springer.Google Scholar
Gomes, J. P. & Lienhart, H. 2010b Time-phase resolved optical measurements on two-dimensional FSI problems. Phys. Procedia 5, 679–688.Google Scholar
Gomes, J. P., Yigit, S., Lienhart, H. & Schäfer, M. 2010 Experimental and numerical study on a laminar fluid–structure interaction reference test case. J. Fluids Struct. 27 (1), 43–61.CrossRefGoogle Scholar
Komatsu, S. & Kobayashi, H. 1980 Vortex-induced oscillation of bluff cylinders. J. Wind Engng Ind. Aerodyn. 6, 335–362.Google Scholar
Knisely, C. W. 1990 Strouhal numbers of rectangular cylinders at incidence: a review and new data. J. Fluids Struct. 4, 371–393.Google Scholar
Nakamura, Y., Ohya, Y. & Tsuruta, H. 1991 Experiments on vortex shedding from flat plates with square leading and trailing edges. J. Fluid Mech. 222, 437–447.Google Scholar
Naudascher, E. & Rockwell, D. 1991 Hydrodaynamic forces. In IAHR Hydrodynamic Structures Design Manual, Vol.3. Balkena.Google Scholar
Naudascher, E. & and Rockwell, D. 1993 Oscillator-model approach to the identification and assessement of flow-induced vibrations in a system. J. Hydraul. Res. 18, 59–82.Google Scholar
Naudascher, E. & Wang, Y. 1993 Flow-induced vibrations of prismatic bodies and grids of prisms. J. Fluids Struct. 7, 341–373.Google Scholar
Parker, R. & Welsh, M. C. 1983 Effects of sound on flow separation from blunt flat plates. Intl J. Heat Fluid Flow 4 (2), 113–127.Google Scholar
Ramberg, S. E. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.Google Scholar
Richter, A. & Naudascher, E. 1976 Fluctuating forces on a rigid circular cylinder in confined flow. J. Fluid Mech. 78, 561–576.Google Scholar
Sarpkaya, T. 1978 Fluid forces on oscillating cylinders. J. Waterway Port Coastal Ocean Div. WW4, 275–290.Google Scholar
Shiraishi, N. & Matsumoto, M. 1983 On classification of vortex-induced oscillation and its application for bridge structures. J. Wind Engng Ind. Aerodyn. 14, 419–430.Google Scholar
Williamson, C. H. K. & Brown, G. L. 1998 A series in $1/ \sqrt{\mathit{Re}} $ to represent the Strouhal–Reynolds number relationship of the cylinder wake. J. Fluids Struct. 12, 1073–1085.Google Scholar
Williamson, C. H. K. & Roshko, A. 1990 Measurements of base pressure in the wake of a cylinder at low Reynolds numbers. Z. Flugwiss. Weltraumforsch. 14, 38–46.Google Scholar