Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T02:51:40.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Electrohydrodynamic instability of miscible core–annular flows with electrical conductivity stratification

Published online by Cambridge University Press:  08 January 2015

Zijing Ding  and
Teck Neng Wong
Zijing Ding*
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Singapore
Teck Neng Wong*
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Singapore
*
†Email addresses for correspondence: [email protected], [email protected].
†Email addresses for correspondence: [email protected], [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the electrohydrodynamical instability of two miscible flows in a micro-pipe subject to an axial electric field. There is an electrical conductivity stratification between the two layers. A weak shear flow arises from a constant axial pressure gradient. The three-dimensional linear stability analysis is studied under the assumption of a quasi-steady state. The influences of the conductivity ratio 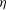${\it\eta}$, the interface location $a$, the interface thickness 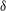${\it\delta}$, the Reynolds number 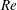$\mathit{Re}$ and the Schmidt number 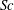$\mathit{Sc}$ on the linear stability of the flows are investigated. The flow becomes more unstable for a larger conductivity contrast. When the conductivity in the inner layer is larger, the critical unstable mode can be dominated by either the corkscrew mode (the azimuthal wavenumber 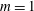$m=1$) or the axisymmetric mode (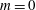$m=0$), which is dependent on the interface location $a$. It is observed that, when the interface is proximal to pipe’s wall, the critical unstable mode shifts from the corkscrew mode to the axisymmetric mode. When the conductivity is larger in the outer layer, the instability is dominated by the axisymmetric mode. A detailed parametric study shows that the flow is least stable when the interface between the two liquids is located at approximately 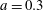$a=0.3$ and 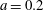$a=0.2$ for conductivity ratios of 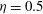${\it\eta}=0.5$ and 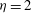${\it\eta}=2$ respectively. The flow becomes more stable as the interface becomes thicker, and the shear flow and ionic diffusion are found to have a stabilizing effect due to the enhancement of dissipation mechanisms.

JFM classification

Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 488 - 512
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baygents, J. C. & Baldessari, F. 1998 Electrohydrodynamic instability in a thin fluid layer with an electrical conductivity gradient. Phys. Fluids 10, 301–311.Google Scholar
Chang, M. H., Ruo, A. C. & Chen, F. 2009 Electrohydrodynamic instability in a horizontal fluid layer with electrical conducivity gradient subject to a weak shear flow. J. Fluid Mech. 634, 191–215.CrossRefGoogle Scholar
Chen, C., Lin, H., Lele, S. K. & Santiago, J. G. 2005 Convective and absolute electrokinetic instability with conductivity gradients. J. Fluid Mech. 524, 263–303.Google Scholar
Conroy, D., Craster, R., Matar, O. & Papageorgiou, D. 2010 Dynamics and stability of an annular electrolyte film. J. Fluid Mech. 656, 481–506.Google Scholar
Conroy, D., Matar, O., Craster, R. & Papageorgiou, D. 2011 Breakup of an electrified jet with charged surfactants. Phys. Fluids 23, 022103.Google Scholar
Conroy, D., Matar, O., Craster, R. & Papageorgiou, D. 2012 Compound viscous thread with electrostatic and electrokinetic effects. J. Fluid Mech. 701, 171–200.Google Scholar
Ding, Z. & Wong, T. N. 2014 Electrohydrodynamic instability in an annular liquid layer with conductivity gradients. Phys. Rev. E 89, 033010.Google Scholar
Ding, Z., Wong, T. N. & Li, H. 2013 Stability of two immiscible leaky-dielectric liquids subjected to a radial electric field in an annulus duct. Phys. Fluids 25, 124103.Google Scholar
Georgiou, E., Papageorriou, D. T., Maldarelli, C. & Rumschitzki, D. S. 1991 The double layer–capillary stability of an annular electrolyte film surrounding a dielectric-fluid core in a tube. J. Fluid Mech. 226, 149–174.Google Scholar
Govindarajan, R. 2004 Effect of miscibility on the linear instability of two-fluid channel flow. Intl J. Multiphase Flow 30, 1177–1192.Google Scholar
Govindarajan, R., L’vov, V. S. & Procaccia, I. 2001 Retardation of the onset of turbulence by minor viscosity contrasts. Phys. Rev. Lett. 87, 174501.Google Scholar
Hohman, M., Shin, M., Rutledge, G. & Brenner, M. 2001 Electrospinning and electrically forced jets. I. Stability theory. Phys. Fluids 13, 2201.Google Scholar
Khorrami, M. 1991 A Chebyshev spectral collocation method using a staggered grid for the stability of cylindrical flows. Intl J. Numer. Meth. Fluids 12, 825–833.Google Scholar
Lin, H. 2009 Electrokinetic instability in microchannel flows: a review. Mech. Res. Commun. 36, 33–38.Google Scholar
Lin, H., Storey, B. D., Oddy, M. H., Chen, C. H. & Santiago, J. G. 2004 Instability of electrokinetic microchannel flows with conductivity gradients. Phys. Fluids 16, 1922–1935.Google Scholar
Melcher, J. 1981 Continuum Electromechanics. MIT.Google Scholar
Melcher, J. & Firebaugh, M. 1967 Travelling-wave bulk electro convection induced across a temperature gradient. Phys. Fluids 10, 1178–1185.Google Scholar
Melcher, J. & Schwartz, W. 1968 Interfacial relaxation overstability in a tangential electric field. Phys. Fluids 11, 2604–2616.Google Scholar
Melcher, J. & Smith, C. 1969 Electrohydrodynamic charge relaxation and interfacial perpendicular-field instability. Phys. Fluids 12, 778–790.Google Scholar
Melstel, A. 1996 Electrohydrodynamic stability of a highly viscous jet. J. Fluid Mech. 312, 311–326.Google Scholar
d’Olce, M., Rakotomalala, N., Salin, D. & Talon, L. 2008 Pearl and mushroom instability patterns in two miscible fluids’ core annular flow. Phys. Fluids 20, 024104.Google Scholar
d’Olce, M., Rakotomalala, N., Salin, D. & Talon, L. 2009 Convective/absolute instability in miscible core–annular flow. Part 1. Experiments. J. Fluid Mech. 618, 305–322.Google Scholar
Ozen, O., Aubry, N., Papageorgiou, D. T. & Petropoulos, P. G. 2006 Monodisperse drop formation in square microchannels. Phys. Rev. Lett. 96, 144501.Google Scholar
Ruo, A. C., Chang, M. H. & Chen, F. 2010 Effect of rotation on the electrohydrodynamic instability of a fluid layer with an electrical conductivity gradient. Phys. Fluids 22, 024102.Google Scholar
Santos, J. J. & Storey, B. D. 2008 Instability of electro-osmotic channel flow with streamwise conductivity gradients. Phys. Rev. E 78, 046316.Google Scholar
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid. 29, 27–64.Google Scholar
Schmid, P. & Henningson, D. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Selvam, B., Merk, S., Govindarajan, R. & Meiburg, E. 2007 Stability of miscible core–annular flows with viscosity stratification. J. Fluid Mech. 592, 23–49.Google Scholar
Selvam, B., Talon, B., Lesshafft, L. & Meiburg, E. 2009 Convective/absolute instability in miscible core–annular flow. Part 2. Numerical simulations and nonlinear global modes. J. Fluid Mech. 618, 323–348.Google Scholar
Sinton, D. & Li, D. 2003 Electroosmotic velocity profiles in microchannels. Colloids Surf. A 222, 273–283.Google Scholar
Storey, B. D., Lin, H. & Santiago, J. G. 2005 Electrokinetic instabilities in thin microchannels. Phys. Fluids 17, 018103.Google Scholar
Talon, L. & Meiburg, E. 2011 Plane Poiseuille flow of miscible layers with different viscosities: instabilities in the Stokes flow regime. J. Fluid Mech. 686, 484–506.Google Scholar
Taylor, G. I. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by an electric field. Proc. R. Soc. Lond. A 291, 159–166.Google Scholar
Wang, Q. M. 2012 Breakup of a poorly conducting liquid thread subject to a radial electric field at zero Reynolds number. Phys. Fluids 24, 102102.CrossRefGoogle Scholar
Yoshikawa, H. N., Crumeyrolle, O. & Mutabazi, I. 2013 Dielectrophoretic force-driven thermal convection in annular geometry. Phys. Fluids 25, 024106.Google Scholar