Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-20T17:13:00.646Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves

Published online by Cambridge University Press:  31 October 2014

Edward Hurst ,
Qiang Yang  and
Yongmann M. Chung
Edward Hurst
Affiliation:
School of Engineering and Centre for Scientific Computing, University of Warwick, Coventry CV4 7AL, UK
Qiang Yang
Affiliation:
School of Engineering and Centre for Scientific Computing, University of Warwick, Coventry CV4 7AL, UK
Yongmann M. Chung*
Affiliation:
School of Engineering and Centre for Scientific Computing, University of Warwick, Coventry CV4 7AL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper exploits the turbulent flow control method using streamwise travelling waves (Quadrio et al. J. Fluid Mech., vol. 627, 2009, pp. 161–178) to study the effect of Reynolds number on turbulent skin-friction drag reduction. Direct numerical simulations (DNS) of a turbulent channel flow subjected to the streamwise travelling waves of spanwise wall velocity have been performed at Reynolds numbers ranging from 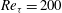$\mathit{Re}_{{\it\tau}}=200$ to 1600. To the best of the authors’ knowledge, this is the highest Reynolds number attempted with DNS for this type of flow control. The present DNS results confirm that the effectiveness of drag reduction deteriorates, and the maximum drag reduction achieved by travelling waves decreases significantly as the Reynolds number increases. The intensity of both the drag reduction and drag increase is reduced with the Reynolds number. Another important finding is that the value of the optimal control parameters changes, even in wall units, when the Reynolds number is increased. This trend is observed for the wall oscillation, stationary wave, and streamwise travelling wave cases. This implies that, when the control parameters used are close to optimal values found at a lower Reynolds number, the drag reduction deteriorates rapidly with increased Reynolds number. In this study, the effect of Reynolds number for the travelling wave is quantified using a scaling in the form 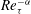$\mathit{Re}_{{\it\tau}}^{-{\it\alpha}}$. No universal constant is found for the scaling parameter ${\it\alpha}$. Instead, the scaling parameter ${\it\alpha}$ has a wide range of values depending on the flow control conditions. Further Reynolds number scaling issues are discussed. Turbulent statistics are analysed to explain a weaker drag reduction observed at high Reynolds numbers. The changes in the Stokes layer and also the mean and root-mean-squared (r.m.s.) velocity with the Reynolds number are also reported. The Reynolds shear stress analysis suggests an interesting possibility of a finite drag reduction at very high Reynolds numbers.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 28 - 55
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Bandyopadhyay, P. R. 2006 Stokes mechanism of drag reduction. Trans. ASME, Ser. E: J. Appl. Mech. 73 (3), 483–489.Google Scholar
Baron, A. & Quadrio, M. 1996 Turbulent drag reduction by spanwise wall oscillation. Appl. Sci. Res. 55, 311–326.CrossRefGoogle Scholar
Berger, T. W., Kim, J., Lee, C. & Lim, J. 2000 Turbulent boundary layer control utilizing the Lorentz force. Phys. Fluids 12 (3), 631–649.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $\mathit{Re}_{{\it\tau}}=4000$ . J. Fluid Mech. 742, 171–191.Google Scholar
Bieler, H., Abbas, A., Chiaramonte, J.-Y. & Sawyers, D.2006 Flow control for aircraft performance enhancements – overview of Airbus–university cooperation. AIAA Paper 2006-3692.CrossRefGoogle Scholar
Bogard, D. G., Ball, K. S. & Wassen, E.2000 Drag reduction for turbulent boundary layer flows using an oscillating wall. AFOSR. The University of Texas at Austin.Google Scholar
Chang, Y., Collis, S. S. & Ramakrishnan, S. 2002 Viscous effects in control of near-wall turbulence. Phys. Fluids 14 (11), 4069–4080.Google Scholar
Choi, K.-S. 2002 Near-wall structure of turbulent boundary layer with spanwise-wall oscillation. Phys. Fluids 14 (7), 2530–2542.Google Scholar
Choi, K.-S., DeBisschop, J.-R. & Clayton, B. R. 1998 Turbulent boundary-layer control by means of spanwise-wall oscillation. AIAA J. 36 (7), 1157–1163.Google Scholar
Choi, K.-S. & Graham, M. 1998 Drag reduction of turbulent pipe flows by circular-wall oscillation. J. Comput. Phys. 10 (1), 7–9.Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Choi, J. I., Xu, C. X. & Sung, H. J. 2002 Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA J. 40 (5), 842–850.CrossRefGoogle Scholar
Chung, Y. M. & Hurst, E. 2014 Turbulent drag reduction at high Reynolds numbers. In Fluid–Structure–Sound Interactions and Control (ed. Zhou, Y., Liu, Y., Huang, L. & Hodges, D. H.), pp. 95–99. Springer.CrossRefGoogle Scholar
Chung, Y. M. & Talha, T. 2011 Effectiveness of active flow control for turbulent skin friction drag reduction. Phys. Fluids 23 (2), 025102.Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100 (2), 215–223.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dhanak, M. R. & Si, C. 1999 On reduction of turbulent wall friction through spanwise wall oscillations. J. Fluid Mech. 383, 175–195.Google Scholar
El-Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Gatti, D. & Quadrio, M. 2013 Performance losses of drag-reducing spanwise forcing at moderate values of the Reynolds number. Phys. Fluids 25 (12), 125109.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re}_{{\it\tau}}=2003$ . Phys. Fluids 18 (1), 011702.Google Scholar
Iwamoto, K., Fukagata, K., Kasagi, N. & Suzuki, Y. 2005 Friction drag reduction achievable by near-wall turbulence manipulation at high Reynolds numbers. Phys. Fluids 17 (1), 011702.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23 (5), 678–689.Google Scholar
Jewkes, J. W., Chung, Y. M. & Carpenter, P. W. 2011 Modification to a turbulent inflow generation method for boundary layer flows. AIAA J. 49 (1), 247–250.CrossRefGoogle Scholar
Jung, S. Y. & Chung, Y. M. 2012 Large-eddy simulations of accelerated turbulent flow in a circular pipe. Intl J. Heat Fluid Flow 33 (1), 1–8.Google Scholar
Jung, W. J., Mangiavacchi, N. & Akhavan, R. 1992 Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys. Fluids A 4 (8), 1605–1607.CrossRefGoogle Scholar
Karniadakis, G. E. & Choi, K.-S. 2003 Mechanisms on transverse motions in turbulent wall flows. Annu. Rev. Fluid Mech. 35, 45–62.Google Scholar
Kim, K., Baek, S.-J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Laadhari, F. 2007 Reynolds number effect on the dissipation function in wall-bounded flows. Phys. Fluids 19 (3), 038101.Google Scholar
Laadhari, F., Skandaji, L. & Morel, R. 1994 Turbulence reduction in a boundary layer by local spanwise oscillating surface. Phys. Fluids 6 (10), 3218–3220.Google Scholar
Laizet, S. & Li, N. 2011 Incompact3d: a powerful tool to tackle turbulence problems with up to $O(10^{5})$ computational cores. Intl J. Numer. Meth. Fluids 67 (11), 1735–1757.Google Scholar
Lardeau, S. & Leschziner, M. A. 2013 The streamwise drag-reduction response of a boundary layer subjected to a sudden imposition of transverse oscillatory wall motion. Phys. Fluids 25 (7), 075109.Google Scholar
Moser, R., Kim, J. & Mansour, N. 1999 Direct numerical simulation of turbulent channel flow up to $\mathit{Re}_{{\it\tau}}=590$ . Phys. Fluids 11 (4), 943–945.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20 (10), 101518.Google Scholar
Nikitin, N. 2000 On the mechanism of turbulence supression by spanwise surface oscillations. Fluid Dyn. 35 (2), 185–190.Google Scholar
Orlandi, P. & Fatica, M. 1997 Direct simulations of turbulent flow in a pipe rotating about its axis. J. Fluid Mech. 343, 43–72.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25 (2), 021704.Google Scholar
Quadrio, M. & Ricco, P. 2003 Initial response of a turbulent channel flow to spanwise oscillation of the walls. J. Turbul. 4, 007.Google Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.Google Scholar
Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.Google Scholar
Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.CrossRefGoogle Scholar
Ricco, P., Ottonelli, C., Hasegawa, Y. & Quadrio, M. 2012 Changes in turbulent dissipation in a channel flow with oscillating walls. J. Fluid Mech. 700, 77–104.CrossRefGoogle Scholar
Ricco, P. & Quadrio, M. 2008 Wall-oscillation conditions for drag reduction in turbulent channel flow. Intl J. Heat Fluid Flow 29 (4), 891–902.CrossRefGoogle Scholar
Ricco, P. & Wu, S. 2004 On the effects of lateral wall oscillations on a turbulent boundary layer. Exp. Therm. Fluid Sci. 29, 41–52.Google Scholar
Schlichting, H. 1968 Boundary Layer Theory, 8th edn. McGraw-Hill.Google Scholar
Sillero, J., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to ${\it\delta}^{+}\approx 2000$ . Phys. Fluids 25, 105102.Google Scholar
Skote, M. 2012 Temporal and spatial transients in turbulent boundary layer flow over an oscillating wall. Intl J. Heat Fluid Flow 38, 1–12.Google Scholar
Skote, M. 2013 Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows. J. Fluid Mech. 730, 273–294.Google Scholar
Spalart, P. R. & McLean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. A 369, 1156–1569.Google Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effect in the overlap region and the mean velocity in turbulent pipe and channel flow. In Self Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), vol. 15. WIT Press.Google Scholar
Tanahashi, M., Kang, S. J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to $\mathit{Re}_{{\it\tau}}=800$ . Intl J. Heat Fluid Flow 25 (3), 331–340.Google Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.Google Scholar
Trujillo, S. M., Bogard, D. G. & Ball, K. S.1997 Turbulent boundary layer drag reduction using an oscillating wall. AIAA Paper 97-1870.Google Scholar
Viotti, C., Quadrio, M. & Luchini, P. 2009 Streamwise oscillation of spanwise velocity at the wall of a channel for turbulent drag reduction. Phys. Fluids 21 (11), 115109.Google Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
Xu, C. X. & Huang, W. X. 2005 Transient response of Reynolds stress transport to spanwise wall oscillation in a turbulent channel flow. Phys. Fluids 17, 018101.Google Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 12 (9), 1–17.Google Scholar