Published online by Cambridge University Press: 03 September 2014
Simplified equations are derived for a granular flow in the ‘dense’ limit where the volume fraction is close to that for dynamical arrest, and the ‘shallow’ limit where the stream-wise length for flow development (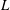 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$) is large compared with the cross-stream height (
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$) is large compared with the cross-stream height (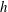 $h$). The mass and diameter of the particles are set equal to 1 in the analysis without loss of generality. In the dense limit, the equations are simplified by taking advantage of the power-law divergence of the pair distribution function
$h$). The mass and diameter of the particles are set equal to 1 in the analysis without loss of generality. In the dense limit, the equations are simplified by taking advantage of the power-law divergence of the pair distribution function 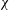 $\chi $ proportional to
$\chi $ proportional to 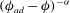 $(\phi _{ad} - \phi )^{- \alpha }$, and a faster divergence of the derivative
$(\phi _{ad} - \phi )^{- \alpha }$, and a faster divergence of the derivative 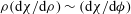 $\rho (\mathrm{d} \chi / \mathrm{d} \rho ) \sim (\mathrm{d} \chi / \mathrm{d} \phi )$, where
$\rho (\mathrm{d} \chi / \mathrm{d} \rho ) \sim (\mathrm{d} \chi / \mathrm{d} \phi )$, where 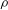 $\rho $ and
$\rho $ and 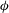 $\phi $ are the density and volume fraction, and
$\phi $ are the density and volume fraction, and 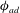 $\phi _{ad}$ is the volume fraction for arrested dynamics. When the height
$\phi _{ad}$ is the volume fraction for arrested dynamics. When the height 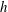 $h$ is much larger than the conduction length, the energy equation reduces to an algebraic balance between the rates of production and dissipation of energy, and the stress is proportional to the square of the strain rate (Bagnold law). In the shallow limit, the stress reduces to a simplified Bagnold stress, where all components of the stress are proportional to
$h$ is much larger than the conduction length, the energy equation reduces to an algebraic balance between the rates of production and dissipation of energy, and the stress is proportional to the square of the strain rate (Bagnold law). In the shallow limit, the stress reduces to a simplified Bagnold stress, where all components of the stress are proportional to 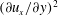 $(\partial u_x/\partial y)^2$, which is the cross-stream (
$(\partial u_x/\partial y)^2$, which is the cross-stream (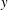 $y$) derivative of the stream-wise (
$y$) derivative of the stream-wise ( $x$) velocity. In the simplified equations for dense shallow flows, the inertial terms are neglected in the
$x$) velocity. In the simplified equations for dense shallow flows, the inertial terms are neglected in the 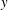 $y$ momentum equation in the shallow limit because the are
$y$ momentum equation in the shallow limit because the are 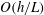 $O(h/L)$ smaller than the divergence of the stress. The resulting model contains two equations, a mass conservation equations which reduces to a solenoidal condition on the velocity in the incompressible limit, and a stream-wise momentum equation which contains just one parameter
$O(h/L)$ smaller than the divergence of the stress. The resulting model contains two equations, a mass conservation equations which reduces to a solenoidal condition on the velocity in the incompressible limit, and a stream-wise momentum equation which contains just one parameter 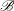 $\mathcal{B}$ which is a combination of the Bagnold coefficients and their derivatives with respect to volume fraction. The leading-order dense shallow flow equations, as well as the first correction due to density variations, are analysed for two representative flows. The first is the development from a plug flow to a fully developed Bagnold profile for the flow down an inclined plane. The analysis shows that the flow development length is
$\mathcal{B}$ which is a combination of the Bagnold coefficients and their derivatives with respect to volume fraction. The leading-order dense shallow flow equations, as well as the first correction due to density variations, are analysed for two representative flows. The first is the development from a plug flow to a fully developed Bagnold profile for the flow down an inclined plane. The analysis shows that the flow development length is 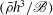 $(\bar{\rho }h^3 / \mathcal{B})$, where
$(\bar{\rho }h^3 / \mathcal{B})$, where 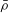 $\bar{\rho }$ is the mean density, and this length is numerically estimated from previous simulation results. The second example is the development of the boundary layer at the base of the flow when a plug flow (with a slip condition at the base) encounters a rough base, in the limit where the momentum boundary layer thickness is small compared with the flow height. Analytical solutions can be found only when the stream-wise velocity far from the surface varies as
$\bar{\rho }$ is the mean density, and this length is numerically estimated from previous simulation results. The second example is the development of the boundary layer at the base of the flow when a plug flow (with a slip condition at the base) encounters a rough base, in the limit where the momentum boundary layer thickness is small compared with the flow height. Analytical solutions can be found only when the stream-wise velocity far from the surface varies as 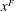 $x^F$, where
$x^F$, where  $x$ is the stream-wise distance from the start of the rough base and
$x$ is the stream-wise distance from the start of the rough base and 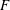 $F$ is an exponent. The boundary layer thickness increases as
$F$ is an exponent. The boundary layer thickness increases as 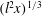 $(l^2 x)^{1/3}$ for all values of
$(l^2 x)^{1/3}$ for all values of 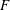 $F$, where the length scale
$F$, where the length scale 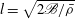 $l = \sqrt{2 \mathcal{B}/ \bar{\rho }}$. The analysis reveals important differences between granular flows and the flows of Newtonian fluids. The Reynolds number (ratio of inertial and viscous terms) turns out to depend only on the layer height and Bagnold coefficients, and is independent of the flow velocity, because both the inertial terms in the conservation equations and the divergence of the stress depend on the square of the velocity/velocity gradients. The compressibility number (ratio of the variation in volume fraction and mean volume fraction) is independent of the flow velocity and layer height, and depends only on the volume fraction and Bagnold coefficients.
$l = \sqrt{2 \mathcal{B}/ \bar{\rho }}$. The analysis reveals important differences between granular flows and the flows of Newtonian fluids. The Reynolds number (ratio of inertial and viscous terms) turns out to depend only on the layer height and Bagnold coefficients, and is independent of the flow velocity, because both the inertial terms in the conservation equations and the divergence of the stress depend on the square of the velocity/velocity gradients. The compressibility number (ratio of the variation in volume fraction and mean volume fraction) is independent of the flow velocity and layer height, and depends only on the volume fraction and Bagnold coefficients.