Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T05:00:20.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical regime of gravity currents flowing in non-rectangular channels with density stratification

Published online by Cambridge University Press:  14 February 2018

L. Chiapponi Open the ORCID record for L. Chiapponi [Opens in a new window] ,
M. Ungarish Open the ORCID record for M. Ungarish [Opens in a new window] ,
S. Longo Open the ORCID record for S. Longo [Opens in a new window] ,
V. Di Federico Open the ORCID record for V. Di Federico [Opens in a new window]  and
F. Addona
L. Chiapponi*
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
M. Ungarish
Affiliation:
Department of Computer Science, Technion, Israel Institute of Technology, Haifa 32000, Israel
S. Longo
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
V. Di Federico
Affiliation:
Dipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Università di Bologna, Viale Risorgimento, 2, 40136 Bologna, Italy
F. Addona
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present theoretical and experimental analyses of the critical condition where the inertial–buoyancy or viscous–buoyancy regime is preserved in a uniform-density gravity current (which propagates over a horizontal plane) of time-variable volume 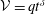${\mathcal{V}}=qt^{\unicode[STIX]{x1D6FF}}$ in a power-law cross-section (with width described by 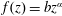$f(z)=bz^{\unicode[STIX]{x1D6FC}}$, where $z$ is the vertical coordinate, 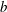$b$ and 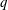$q$ are positive real numbers, and $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FF}$ are non-negative real numbers) occupied by homogeneous or linearly stratified ambient fluid. The magnitude of the ambient stratification is represented by the parameter 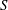$S$, with 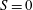$S=0$ and 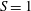$S=1$ describing the homogeneous and maximum stratification cases respectively. Earlier theoretical and experimental results valid for a rectangular cross-section (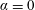$\unicode[STIX]{x1D6FC}=0$) and uniform ambient fluid are generalized here to a power-law cross-section and stratified ambient. Novel time scalings, obtained for inertial and viscous regimes, allow a derivation of the critical flow parameter 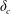$\unicode[STIX]{x1D6FF}_{c}$ and the corresponding propagation rate as 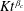$Kt^{\unicode[STIX]{x1D6FD}_{c}}$ as a function of the problem parameters. Estimates of the transition length between the inertial and viscous regimes are also derived. A series of experiments conducted in a semicircular cross-section (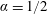$\unicode[STIX]{x1D6FC}=1/2$) validate the critical values 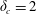$\unicode[STIX]{x1D6FF}_{c}=2$ and 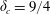$\unicode[STIX]{x1D6FF}_{c}=9/4$ for the two cases 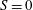$S=0$ and 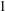$1$. The ratio between the inertial and viscous forces is determined by an effective Reynolds number proportional to 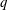$q$ at some power. The threshold value of this number, which enables a determination of the regime of the current (inertial–buoyancy or viscous–buoyancy) in critical conditions, is determined experimentally for both $S=0$ and 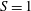$S=1$. We conclude that a very significant generalization of the insights and results from two-dimensional (rectangular cross-section channel) gravity currents to power-law cross-sections is available.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 579 - 612
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Didden, N. & Maxworthy, T. 1982 The viscous spreading of plane and axisymmetric gravity currents. J. Fluid Mech. 121, 27–42.CrossRefGoogle Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Longo, S., Di Federico, V., Archetti, R., Chiapponi, L., Ciriello, V. & Ungarish, M. 2013 On the axisymmetric spreading of non-Newtonian power-law gravity currents of time-dependent volume: an experimental and theoretical investigation focused on the inference of rheological parameters. J. Non-Newtonian Fluid Mech. 201, 69–79.Google Scholar
Longo, S., Di Federico, V. & Chiapponi, L. 2015a Non-Newtonian power-law gravity currents propagating in confining boundaries. Environ. Fluid Mech. 15 (3), 515–535.Google Scholar
Longo, S., Ungarish, M., Di Federico, V., Chiapponi, L. & Addona, F. 2016a Gravity currents in a linearly stratified ambient fluid created by lock release and influx in semi-circular and rectangular channels. Phys. Fluids 28, 1–25.CrossRefGoogle Scholar
Longo, S., Ungarish, M., Di Federico, V., Chiapponi, L. & Addona, F. 2016b Gravity currents produced by constant and time varying inflow in a circular cross-section channel: experiments and theory. Adv. Water Resour. 90, 10–23.Google Scholar
Longo, S., Ungarish, M., Di Federico, V., Chiapponi, L. & Maranzoni, A. 2015b The propagation of gravity currents in a circular cross-section channel: experiments and theory. J. Fluid Mech. 764, 513–537.Google Scholar
Marino, B. M. & Thomas, L. P. 2011 Dam-break release of a gravity current in a power-law channel section. J. Phys.: Conf. Ser. 296, 012008.Google Scholar
Maxworthy, T. 1983 Gravity currents with variable inflow. J. Fluid Mech. 128, 247–257.CrossRefGoogle Scholar
Monaghan, J., Mériaux, C., Huppert, H. & Monaghan, J. 2009 High Reynolds number gravity currents along v-shaped valleys. Eur. J. Mech. (B/Fluids) 28 (5), 651–659.CrossRefGoogle Scholar
Shringarpure, M., Lee, H., Ungarish, M. & Balachandar, S. 2013 Front conditions of high-Re gravity currents produced by constant and time-dependent influx: an analytical and numerical study. Eur. J. Mech. (B/Fluids) 41 (0), 109–122.CrossRefGoogle Scholar
Simpson, J. E. 1997 Gravity Currents in the Environment and the Laboratory. Cambridge University Press.Google Scholar
Takagi, D. & Huppert, H. E. 2007 The effect of confining boundaries on viscous gravity currents. J. Fluid Mech. 577, 495–505.Google Scholar
Takagi, D. & Huppert, H. E. 2008 Viscous gravity currents inside confining channels and fractures. Phys. Fluids 20, 023104.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman & Hall/CRC Press.Google Scholar
Ungarish, M. 2012 A general solution of Benjamin-type gravity current in a channel of non-rectangular cross-section. Environ. Fluid Mech. 12 (3), 251–263.CrossRefGoogle Scholar
Ungarish, M. 2015 Shallow-water solutions for gravity currents in non-rectangular cross-area channels with stratified ambient. Environ. Fluid Mech. 15 (4), 793–820.Google Scholar
Ungarish, M. 2018 Thin-layer models for gravity currents in channels of general cross-section area, a review. Environ. Fluid Mech. 18, 283–333.CrossRefGoogle Scholar
Ungarish, M., Mériaux, C. A. & Kurz-Besson, C. B. 2014 The propagation of gravity currents in a V-shaped triangular cross-section channel: experiments and theory. J. Fluid Mech. 754, 232–249.Google Scholar
Zemach, T. & Ungarish, M. 2013 Gravity currents in non-rectangular cross-section channels: analytical and numerical solutions of the one-layer shallow-water model for high-Reynolds-number propagation. Phys. Fluids 25, 026601.Google Scholar