Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:26:54.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Coupled electrohydrodynamic transport in rough fractures: a generalized lubrication theory

Published online by Cambridge University Press:  17 May 2022

Mainendra Kumar Dewangan ,
Uddipta Ghosh Open the ORCID record for Uddipta Ghosh [Opens in a new window] ,
Tanguy Le Borgne  and
Yves Méheust Open the ORCID record for Yves Méheust [Opens in a new window]
Mainendra Kumar Dewangan
Affiliation:
Discipline of Mechanical Engineering, Indian Institute of Technology Gandhinagar, Palaj 382355, Gujrat, India
Uddipta Ghosh*
Affiliation:
Discipline of Mechanical Engineering, Indian Institute of Technology Gandhinagar, Palaj 382355, Gujrat, India Univ. Rennes, CNRS, Géosciences Rennes (UMR6118), 35042 Rennes, France
Tanguy Le Borgne
Affiliation:
Univ. Rennes, CNRS, Géosciences Rennes (UMR6118), 35042 Rennes, France
Yves Méheust*
Affiliation:
Univ. Rennes, CNRS, Géosciences Rennes (UMR6118), 35042 Rennes, France
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

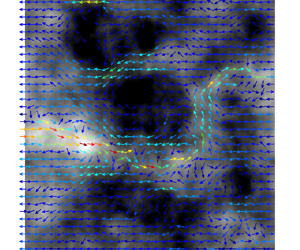
Fractures provide pathways for fluids and solutes through crystalline rocks and low permeability materials, thus playing a key role in many subsurface processes and applications. In small aperture fractures, solute transport is strongly impacted by the coupling of electrical double layers at mineral–fluid interfaces to bulk ion transport. Yet, most models of flow and transport in fractures ignore these effects. Solving such coupled electrohydrodynamics in realistic three-dimensional (3-D) fracture geometries poses computational challenges which have so far limited our understanding of those electro-osmotic effects’ impact. Starting from the Poisson–Nernst–Planck–Navier–Stokes (PNPNS) equations and using a combination of rescaling, asymptotic analysis and the Leibniz rule, we derive a set of nonlinearly coupled conservation equations for the local fluxes of fluid mass, solute mass and electrical charges. Their solution yields the fluid pressure, solute concentration and electrical potential fields. The model is validated by comparing its predictions to the solutions of the PNPNS equations in 3-D rough fractures. Application of the model to realistic rough fracture geometries evidences several phenomena hitherto not reported in the literature, including: (i) a dependence of the permeability and electrical conductivity on the fracture walls’ charge density, (ii) local (sometimes global) flow reversal, and (iii) spatial heterogeneities in the concentration field without any imposed concentration gradient. This new theoretical framework will allow systematically addressing large statistics of fracture geometry realizations of given stochastic parameters, to infer the impact of the geometry and various hydrodynamic and electrical parameters on the coupled transport of fluid and ions in rough fractures.

JFM classification

MHD and Electrohydrodynamics: Electrokinetic flows Low-Reynolds-number flows: Lubrication theory Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A11
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ajdari, A. 1996 Generation of transverse fluid currents and forces by an electric field: electro-osmosis on charge-modulated and undulated surfaces. Phys. Rev. E 53 (5), 4996.CrossRefGoogle ScholarPubMed
Ajdari, A. 2001 Transverse electrokinetic and microfluidic effects in micropatterned channels: lubrication analysis for slab geometries. Phys. Rev. E 65 (1), 016301.CrossRefGoogle ScholarPubMed
Anders, M.H., Laubach, S.E. & Scholz, C.H. 2014 Microfractures: a review. J. Struct. Geol. 69, 377–394.CrossRefGoogle Scholar
Basha, H.A. & El-Asmar, W. 2003 The fracture flow equation and its perturbation solution. Water Resour. Res. 39 (12), 1365.CrossRefGoogle Scholar
Batchelor, G.K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Bazant, M.Z., Kilic, M.S., Storey, B.D. & Ajdari, A. 2009 Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 152 (1–2), 48–88.CrossRefGoogle ScholarPubMed
Bense, V.F., Gleeson, T., Loveless, S.E., Bour, O. & Scibek, J. 2013 Fault zone hydrogeology. Earth Sci. Rev. 127, 171–192.CrossRefGoogle Scholar
Berkowitz, B. 2002 Characterizing flow and transport in fractured geological media: a review. Adv. Water Resour. 25 (8–12), 861–884.CrossRefGoogle Scholar
Boffa, J.M., Allain, C. & Hulin, J.P. 1998 Experimental analysis of fracture rugosity in granular and compact rocks. Eur. Phys. J. Appl. Phys. 2 (3), 281–289.CrossRefGoogle Scholar
Bogdanov, I.I., Mourzenko, V.V., Thovert, J.-F. & Adler, P.M. 2003 Effective permeability of fractured porous media in steady state flow. Water Resour. Res. 39 (1), 1023.CrossRefGoogle Scholar
Bonnet, E., Bour, O., Odling, N.E., Davy, P., Main, I., Cowie, P. & Berkowitz, B. 2001 Scaling of fracture systems in geological media. Rev. Geophys. 39 (3), 347–383.CrossRefGoogle Scholar
Bouchaud, E., Lapasset, G. & Planès, J. 1990 Fractal dimension of fractured surfaces: a universal value? Europhys. Lett. 13, 73–79.CrossRefGoogle Scholar
Bour, O. & Davy, P. 1997 Connectivity of random fault networks following a power law fault length distribution. Water Resour. Res. 33 (7), 1567–1583.CrossRefGoogle Scholar
Brantley, S.L., Goldhaber, M.B. & Ragnarsdottir, K.V. 2007 Crossing disciplines and scales to understand the critical zone. Elements 3 (5), 307–314.CrossRefGoogle Scholar
Bredehoeft, J.D., England, A.W., Stewart, D.B., Trask, N.J. & Winograd, I.J. 1978 Geologic disposal of high-level radioactive wastes: Earth-science perspectives. Tech. Rep. United States Department of the Interior, Geological Survey. https://doi.org/10.3133/cir779.CrossRefGoogle Scholar
Brown, S.R. 1987 Fluid flow through rock joints: the effect of surface roughness. J. Geophys. Res.: Solid Earth 92 (B2), 1337–1347.CrossRefGoogle Scholar
Brown, S.R. 1989 Transport of fluid and electric current through a single fracture. J. Geophys. Res.: Solid Earth 94 (B7), 9429–9438.CrossRefGoogle Scholar
Brown, S.R. 1995 Simple mathematical model of a rough fracture. J. Geophys. Res.: Solid Earth 100 (B4), 5941–5952.CrossRefGoogle Scholar
Brown, S.R. & Bruhn, R.L. 1998 Fluid permeability of deformable fracture networks. J. Geophys. Res.: Solid Earth 103 (B2), 2489–2500.CrossRefGoogle Scholar
Brown, S.R. & Scholz, C.H. 1985 Closure of random elastic surfaces in contact. J. Geophys. Res.: Solid Earth 90 (B7), 5531–5545.CrossRefGoogle Scholar
Brown, S.R., Stockman, H.W. & Reeves, S.J. 1995 Applicability of the Reynolds equation for modeling fluid flow between rough surfaces. Geophys. Res. Lett. 22 (18), 2537–2540.CrossRefGoogle Scholar
Brunet, E. & Ajdari, A. 2004 Generalized Onsager relations for electrokinetic effects in anisotropic and heterogeneous geometries. Phys. Rev. E 69 (1), 016306.CrossRefGoogle ScholarPubMed
Brush, D.J. & Thomson, N.R. 2003 Fluid flow in synthetic rough-walled fractures: Navier–Stokes, Stokes, and local cubic law simulations. Water Resour. Res. 39 (4), 1085.CrossRefGoogle Scholar
Cardenas, M.B., Slottke, D.T., Ketcham, R.A. & Sharp, J.M. 2007 Navier–Stokes flow and transport simulations using real fractures shows heavy tailing due to eddies. Geophys. Res. Lett. 34 (14), L14404.CrossRefGoogle Scholar
Datta, S. & Ghosal, S. 2009 Characterizing dispersion in microfluidic channels. Lab Chip 9 (17), 2537–2550.CrossRefGoogle ScholarPubMed
Detwiler, R.L., Rajaram, H. & Glass, R.J. 2000 Solute transport in variable-aperture fractures: an investigation of the relative importance of Taylor dispersion and macrodispersion. Water Resour. Res. 36 (7), 1611–1625.CrossRefGoogle Scholar
Drazer, G. & Koplik, J. 2000 Permeability of self-affine rough fractures. Phys. Rev. E 62 (6), 8076.CrossRefGoogle ScholarPubMed
Drazer, G. & Koplik, J. 2002 Transport in rough self-affine fractures. Phys. Rev. E 66 (2), 026303.CrossRefGoogle ScholarPubMed
de Dreuzy, J.R., Davy, P. & Bour, O. 2001 Hydraulic properties of two-dimensional random fracture networks following a power law length distribution – 2. Permeability of networks based on lognormal distribution of apertures. Water Resour. Res. 37 (8), 2079–2095.CrossRefGoogle Scholar
de Dreuzy, J.-R., Davy, P. & Bour, O. 2002 Hydraulic properties of two-dimensional random fracture networks following power law distributions of length and aperture. Water Resour. Res. 38 (12), 1–12.CrossRefGoogle Scholar
de Dreuzy, J.-R., Méheust, Y. & Pichot, G. 2012 Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res.: Solid Earth 117 (B11), B11207.Google Scholar
Gamson, P.D., Beamish, B.B. & Johnson, D.P. 1993 Coal microstructure and micropermeability and their effects on natural gas recovery. Fuel 72 (1), 87–99.CrossRefGoogle Scholar
Ghosal, S. 2002 Lubrication theory for electro-osmotic flow in a microfluidic channel of slowly varying cross-section and wall charge. J. Fluid Mech. 459, 103–128.CrossRefGoogle Scholar
Ghosal, S. 2003 The effect of wall interactions in capillary-zone electrophoresis. J. Fluid Mech. 491, 285–300.CrossRefGoogle Scholar
Ghosh, U., Chaudhury, K. & Chakraborty, S. 2016 Electroosmosis over non-uniformly charged surfaces: modified smoluchowski slip velocity for second-order fluids. J. Fluid Mech. 809, 664–690.CrossRefGoogle Scholar
Ghosh, U., Le Borgne, T., Jougnot, D., Linde, N. & Méheust, Y. 2018 Geoelectrical signatures of reactive mixing: a theoretical assessment. Geophys. Res. Lett. 45 (8), 3489–3498.CrossRefGoogle Scholar
Ghosh, U., Mandal, S. & Chakraborty, S. 2017 Electroosmosis over charge-modulated surfaces with finite electrical double layer thicknesses: asymptotic and numerical investigations. Phys. Rev. Fluids 2 (6), 064203.CrossRefGoogle Scholar
Grisak, G.E. & Pickens, J.-F. 1980 Solute transport through fractured media: 1. The effect of matrix diffusion. Water Resour. Res. 16 (4), 719–730.CrossRefGoogle Scholar
Hamzehpour, H., Atakhani, A., Gupta, A.K. & Sahimi, M. 2014 Electro-osmotic flow in disordered porous and fractured media. Phys. Rev. E 89 (3), 033007.CrossRefGoogle ScholarPubMed
Hunter, R.J. 2013 Zeta Potential in Colloid Science: Principles and Applications, vol. 2. Academic Press.Google Scholar
Ishido, T. & Mizutani, H. 1981 Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics. J. Geophys. Res.: Solid Earth 86 (B3), 1763–1775.CrossRefGoogle Scholar
Javadi, M., Sharifzadeh, M. & Shahriar, K. 2010 A new geometrical model for non-linear fluid flow through rough fractures. J. Hydrol. 389 (1–2), 18–30.CrossRefGoogle Scholar
Jougnot, D. & Linde, N. 2013 Self-potentials in partially saturated media: the importance of explicit modeling of electrode effects. Vadose Zone J. 12, 1–21.CrossRefGoogle Scholar
Karniadakis, G., Beskok, A. & Aluru, N. 2006 Microflows and Nanoflows: Fundamentals and Simulation, vol. 29. Springer Science & Business Media.Google Scholar
Kessouri, P., et al. 2019 Induced polarization applied to biogeophysics: recent advances and future prospects. Near Surf. Geophys. 17 (6-Recent Developments in Induced Polarization), 595–621.CrossRefGoogle Scholar
Khair, A.S. & Squires, T.M. 2008 Fundamental aspects of concentration polarization arising from nonuniform electrokinetic transport. Phys. Fluids 20 (8), 087102.CrossRefGoogle Scholar
Kilic, M.S., Bazant, M.Z. & Ajdari, A. 2007 Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson–Nernst–Planck equations. Phys. Rev. E 75 (2), 021503.CrossRefGoogle ScholarPubMed
Konzuk, J.S. & Kueper, B.H. 2004 Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture. Water Resour. Res. 40 (2), W02402.CrossRefGoogle Scholar
Koyama, T., Neretnieks, I. & Jing, L. 2008 A numerical study on differences in using Navier–Stokes and Reynolds equations for modeling the fluid flow and particle transport in single rock fractures with shear. Intl J. Rock Mech. Min. Sci. 45 (7), 1082–1101.CrossRefGoogle Scholar
de La Vaissière, R., Armand, G. & Talandier, J. 2015 Gas and water flow in an excavation-induced fracture network around an underground drift: a case study for a radioactive waste repository in clay rock. J. Hydrol. 521, 141–156.CrossRefGoogle Scholar
Leal, L.G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, vol. 7. Cambridge University Press.CrossRefGoogle Scholar
Ledésert, B., Hebert, R., Genter, A., Bartier, D., Clauer, N. & Grall, C. 2010 Fractures, hydrothermal alterations and permeability in the Soultz enhanced geothermal system. C. R. Géosci. 342 (7–8), 607–615.CrossRefGoogle Scholar
Linde, N., Jougnot, D., Revil, A., Matthäi, S.K., Arora, T., Renard, D. & Doussan, C. 2007 Streaming current generation in two-phase flow conditions. Geophys. Res. Lett. 34 (3), L03306.CrossRefGoogle Scholar
Long, J., Gilmour, P. & Witherspoon, P.A. 1985 A model for steady fluid flow in random three-dimensional networks of disc-shaped fractures. Water Resour. Res. 21 (8), 1105–1115.CrossRefGoogle Scholar
López, J.M.G., Bauluz, B., Fernández-Nieto, C. & Oliete, A.Y. 2005 Factors controlling the trace-element distribution in fine-grained rocks: the albian kaolinite-rich deposits of the Oliete Basin (NE Spain). Chem. Geol. 214 (1–2), 1–19.CrossRefGoogle Scholar
MacQuarrie, K.T.B. & Mayer, K.U. 2005 Reactive transport modeling in fractured rock: a state-of-the-science review. Earth Sci. Rev. 72 (3–4), 189–227.CrossRefGoogle Scholar
Marino, S., Coelho, D., Bekri, S. & Adler, P.M. 2000 Electroosmotic phenomena in fractures. J. Colloid Interface Sci. 223 (2), 292–304.CrossRefGoogle ScholarPubMed
Marino, S., Shapiro, M. & Adler, P.M. 2001 Coupled transports in heterogeneous media. J. Colloid Interface Sci. 243 (2), 391–419.CrossRefGoogle Scholar
Marshall, D.J. & Madden, T.R. 1959 Induced polarization, a study of its causes. Geophysics 24 (4), 790–816.CrossRefGoogle Scholar
Méheust, Y. & Schmittbuhl, J. 2000 Flow enhancement of a rough fracture. Geophys. Res. Lett. 27 (18), 2989–2992.CrossRefGoogle Scholar
Méheust, Y. & Schmittbuhl, J. 2001 Geometrical heterogeneities and permeability anisotropy of rough fractures. J. Geophys. Res.: Solid Earth 106 (B2), 2089–2102.CrossRefGoogle Scholar
Méheust, Y. & Schmittbuhl, J. 2003 Scale effects related to flow in rough fractures. Pure Appl. Geophys. 160 (5–6), 1023–1050.CrossRefGoogle Scholar
Molinero, J. & Samper, J. 2006 Large-scale modeling of reactive solute transport in fracture zones of granitic bedrocks. J. Contam. Hydrol. 82 (3–4), 293–318.CrossRefGoogle ScholarPubMed
Mondal, P.K. & Sleep, B.E. 2012 Colloid transport in dolomite rock fractures: effects of fracture characteristics, specific discharge, and ionic strength. Environ. Sci. Technol. 46 (18), 9987–9994.CrossRefGoogle ScholarPubMed
Mourzenko, V.V., Thovert, J.-F. & Adler, P.M. 1995 Permeability of a single fracture; validity of the Reynolds equation. J. Phys. II 5 (3), 465–482.Google Scholar
Neuzil, C.E. & Tracy, J.V. 1981 Flow through fractures. Water Resour. Res. 17 (1), 191–199.CrossRefGoogle Scholar
Nicholl, M.J., Rajaram, H., Glass, R.J. & Detwiler, R. 1999 Saturated flow in a single fracture: evaluation of the Reynolds equation in measured aperture fields. Water Resour. Res. 35 (11), 3361–3373.CrossRefGoogle Scholar
O'connor, J.T., et al. 1965 A classification for quartz-rich igneous rocks based on feldspar ratios. US Geol. Surv. Prof. Paper B 525, 79–84.Google Scholar
Onsager, L. 1931 a Reciprocal relations in irreversible processes. I. Phys. Rev. 37 (4), 405.CrossRefGoogle Scholar
Onsager, L. 1931 b Reciprocal relations in irreversible processes. II. Phys. Rev. 38 (12), 2265.CrossRefGoogle Scholar
Painter, S. & Cvetkovic, V. 2005 Upscaling discrete fracture network simulations: an alternative to continuum transport models. Water Resour. Res. 41 (2), W02002.CrossRefGoogle Scholar
Park, S.Y., Russo, C.J., Branton, D. & Stone, H.A. 2006 Eddies in a bottleneck: an arbitrary Debye length theory for capillary electroosmosis. J. Colloid Interface Sci. 297 (2), 832–839.CrossRefGoogle Scholar
Patankar, S. 1980 Numerical Heat Transfer and Fluid Flow. CRC.Google Scholar
Pettijohn, F.J. 1957 Sedimentary Rocks, vol. 2. Harper & Brothers.Google Scholar
Renard, P. & Allard, D. 2013 Connectivity metrics for subsurface flow and transport. Adv. Water Resour. 51, 168–196.CrossRefGoogle Scholar
Revil, A. & Florsch, N. 2010 Determination of permeability from spectral induced polarization in granular media. Geophys. J. Intl 181 (3), 1480–1498.Google Scholar
Revil, A., Linde, N., Cerepi, A., Jougnot, D., Matthäi, S. & Finsterle, S. 2007 Electrokinetic coupling in unsaturated porous media. J. Colloid Interface Sci. 313 (1), 315–327.CrossRefGoogle ScholarPubMed
Revil, A. & Pessel, M. 2002 Electroosmotic flow and the validity of the classical Darcy equation in silty shales. Geophys. Res. Lett. 29 (9), 14–1.CrossRefGoogle Scholar
Revil, A., Schwaeger, H., Cathles, L.M. & Manhardt, P.D. 1999 Streaming potential in porous media: 2. Theory and application to geothermal systems. J. Geophys. Res.: Solid Earth 104 (B9), 20033–20048.CrossRefGoogle Scholar
Rojas, S. & Koplik, J. 1998 Nonlinear flow in porous media. Phys. Rev. E 58 (4), 4776.CrossRefGoogle Scholar
Rosanne, M., Paszkuta, M., Thovert, J.-F. & Adler, P.M. 2004 Electro-osmotic coupling in compact clays. Geophys. Res. Lett. 31 (18), L18614.CrossRefGoogle Scholar
Roux, S., Plouraboué, F. & Hulin, J.-P. 1998 Tracer dispersion in rough open cracks. Transp. Porous Media 32 (1), 97–116.CrossRefGoogle Scholar
Saville, D.A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9 (1), 321–337.CrossRefGoogle Scholar
Schmittbuhl, J., Schmitt, F. & Scholz, C. 1995 Scaling invariance of crack surfaces. J. Geophys. Res.: Solid Earth 100 (B4), 5953–5973.CrossRefGoogle Scholar
Schmuck, M. & Bazant, M.Z. 2015 Homogenization of the Poisson–Nernst–Planck equations for ion transport in charged porous media. SIAM J. Appl. Maths 75 (3), 1369–1401.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012 Strong-field electrophoresis. J. Fluid Mech. 701, 333–351.CrossRefGoogle Scholar
Squires, T.M. & Quake, S.R. 2005 Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 77 (3), 977.CrossRefGoogle Scholar
Tanksley, M.A. & Koplik, J. 1994 Path-integral variational methods for flow through porous media. Phys. Rev. E 49 (2), 1353.CrossRefGoogle ScholarPubMed
Teutli-León, M.M., Oropeza, M.T., González, I. & Soria, A. 2005 Mathematical modeling of a galvanostatic soil electroremediation process. AIChE J. 51 (6), 1822–1833.CrossRefGoogle Scholar
Thompson, M.E. 1991 Numerical simulation of solute transport in rough fractures. J. Geophys. Res.: Solid Earth 96 (B3), 4157–4166.CrossRefGoogle Scholar
Thompson, M.E. & Brown, S.R. 1991 The effect of anisotropic surface roughness on flow and transport in fractures. J. Geophys. Res.: Solid Earth 96 (B13), 21923–21932.CrossRefGoogle Scholar
Tripathi, D., Narla, V.K. & Aboelkassem, Y. 2020 Electrokinetic membrane pumping flow model in a microchannel. Phys. Fluids 32 (8), 082004.CrossRefGoogle Scholar
Tsang, Y.W. 1984 The effect of tortuosity on fluid flow through a single fracture. Water Resour. Res. 20 (9), 1209–1215.CrossRefGoogle Scholar
Wang, J., Hu, H., Guan, W. & Li, H. 2015 a Electrokinetic experimental study on saturated rock samples: zeta potential and surface conductance. Geophys. J. Intl 201 (2), 869–877.CrossRefGoogle Scholar
Wang, J.S.Y., Narasimhan, T.N. & Scholz, C.H. 1988 Aperture correlation of a fractal fracture. J. Geophys. Res.: Solid Earth 93 (B3), 2216–2224.CrossRefGoogle Scholar
Wang, L., Cardenas, M.B., Slottke, D.T., Ketcham, R.A. & Sharp, J.M. 2015 b Modification of the local cubic law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 51 (4), 2064–2080.CrossRefGoogle Scholar
Wang, M. & Revil, A. 2010 Electrochemical charge of silica surfaces at high ionic strength in narrow channels. J. Colloid Interface Sci. 343 (1), 381–386.CrossRefGoogle ScholarPubMed
Watanabe, N., Hirano, N. & Tsuchiya, N. 2008 Determination of aperture structure and fluid flow in a rock fracture by high-resolution numerical modeling on the basis of a flow-through experiment under confining pressure. Water Resour. Res. 44 (6), W06412.CrossRefGoogle Scholar
Wendland, E. & Himmelsbach, T. 2002 Transport simulation with stochastic aperture for a single fracture–comparison with a laboratory experiment. Adv. Water Resour. 25 (1), 19–32.CrossRefGoogle Scholar
Wong, P.-Z., Koplik, J. & Tomanic, J.P. 1984 Conductivity and permeability of rocks. Phys. Rev. B 30 (11), 6606.CrossRefGoogle Scholar
Yan, Y. & Koplik, J. 2008 Flow of power-law fluids in self-affine fracture channels. Phys. Rev. E 77 (3), 036315.CrossRefGoogle ScholarPubMed
Yeo, I.W., De Freitas, M.H. & Zimmerman, R.W. 1998 Effect of shear displacement on the aperture and permeability of a rock fracture. Intl J. Rock Mech. Min. Sci. 35 (8), 1051–1070.CrossRefGoogle Scholar
Zimmerman, R.W., Kumar, S. & Bodvarsson, G.S. 1991 Lubrication theory analysis of the permeability of rough-walled fractures. Intl J. Rock Mech. Min. Sci. Geomech. Abstr. 28 (4), 325–331.Google Scholar
Zimmerman, R.W. & Bodvarsson, G.S. 1996 Hydraulic conductivity of rock fractures. Transp. Porous Media 23 (1), 1–30.CrossRefGoogle Scholar
Supplementary material: File

Dewangan et al. supplementary material

Dewangan et al. supplementary material

Download Dewangan et al. supplementary material(File)
File 2.8 MB