Published online by Cambridge University Press: 26 January 2017
This work compares the enstrophy with the scalar dissipation rate, as well as the passive scalar variance with the turbulent kinetic energy, in the presence of coherent Kármán vortices in the intermediate wake of a circular cylinder. Measurements are made at 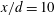 $x/d=10$, 20 and 40, where
$x/d=10$, 20 and 40, where  $x$ is the streamwise distance from the cylinder axis and
$x$ is the streamwise distance from the cylinder axis and 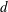 $d$ is the cylinder diameter, with a Reynolds number of
$d$ is the cylinder diameter, with a Reynolds number of 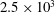 $2.5\times 10^{3}$ based on the cylinder diameter and the free-stream velocity. A probe consisting of eight hot wires (four X-wires) and four cold wires is used to measure simultaneously the three components of the fluctuating velocity and vorticity vectors, as well as the fluctuating temperature gradient vector at nominally the same point in the plane of the mean shear. It is found that the enstrophy and scalar dissipation spectra collapse approximately at all wavenumbers except around the Kármán vortex street wavenumber for
$2.5\times 10^{3}$ based on the cylinder diameter and the free-stream velocity. A probe consisting of eight hot wires (four X-wires) and four cold wires is used to measure simultaneously the three components of the fluctuating velocity and vorticity vectors, as well as the fluctuating temperature gradient vector at nominally the same point in the plane of the mean shear. It is found that the enstrophy and scalar dissipation spectra collapse approximately at all wavenumbers except around the Kármán vortex street wavenumber for 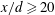 $x/d\geqslant 20$. The spectral similarity between the streamwise velocity fluctuation
$x/d\geqslant 20$. The spectral similarity between the streamwise velocity fluctuation  $u$ and the passive scalar
$u$ and the passive scalar 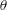 $\unicode[STIX]{x1D703}$ is better than that between the velocity fluctuation vector
$\unicode[STIX]{x1D703}$ is better than that between the velocity fluctuation vector 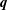 $\boldsymbol{q}$ and
$\boldsymbol{q}$ and 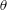 $\unicode[STIX]{x1D703}$. This is closely related to the highly organized lateral velocity fluctuation
$\unicode[STIX]{x1D703}$. This is closely related to the highly organized lateral velocity fluctuation  $v$ in this flow. The present observations are fully consistent with the expectation that small scales of the velocity and temperature fields are more likely to exhibit a close relationship than scales associated with the bulk of the turbulent energy or scalar variance. The variation across the wake of the time scale ratio between scalar and velocity fields is significantly smaller than that of the turbulent Prandtl number.
$v$ in this flow. The present observations are fully consistent with the expectation that small scales of the velocity and temperature fields are more likely to exhibit a close relationship than scales associated with the bulk of the turbulent energy or scalar variance. The variation across the wake of the time scale ratio between scalar and velocity fields is significantly smaller than that of the turbulent Prandtl number.