Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-19T18:29:05.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls

Published online by Cambridge University Press:  04 September 2014

J. F. Torres ,
D. Henry ,
A. Komiya  and
S. Maruyama
J. F. Torres*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France Graduate School of Engineering, Tohoku University, 6-6-04, Aramaki Aza Aoba Aoba-ku, Sendai, Miyagi 980-8579, Japan
D. Henry
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
A. Komiya
Affiliation:
Institute of Fluid Science, Tohoku University, 2-1-1, Katahira, Aoba-ku, Sendai, Miyagi 980-8577, Japan
S. Maruyama
Affiliation:
Institute of Fluid Science, Tohoku University, 2-1-1, Katahira, Aoba-ku, Sendai, Miyagi 980-8577, Japan
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Natural convection in an inclined cubical cavity heated from two opposite walls maintained at different temperatures and with adiabatic sidewalls is investigated numerically. The cavity is inclined by an angle 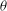$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta $ around a lower horizontal edge and the isothermal wall set at the higher temperature is the lower wall in the horizontal situation (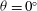$\theta = 0^\circ $). A continuation method developed from a three-dimensional spectral finite-element code is applied to determine the bifurcation diagrams for steady flow solutions. The numerical technique is used to study the influence of 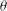${\theta }$ on the stability of the flow for moderate Rayleigh numbers in the range 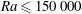$\mathit{Ra} \leq 150\, 000$, focusing on the Prandtl number 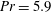$\mathit{Pr} = 5.9$. The results show that the inclination breaks the degeneracy of the stable solutions obtained at the first bifurcation point in the horizontal cubic cavity: (i) the transverse stable rolls, whose rotation vector is in the same direction as the inclination vector 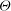${\boldsymbol{\Theta}}$, start from 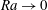$\mathit{Ra} \to 0$ forming a leading branch and becoming more predominant with increasing 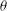$\theta $; (ii) a disconnected branch consisting of transverse rolls, whose rotation vector is opposite to 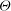${\boldsymbol{\Theta}}$, develops from a saddle-node bifurcation, is stabilized at a pitchfork bifurcation, but globally disappears at a critical inclination angle; (iii) the semi-transverse stable rolls, whose rotation axis is perpendicular to 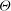${\boldsymbol{\Theta}}$ at 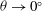$\theta \to 0^\circ $, develop from another saddle-node bifurcation, but the branch also disappears at a critical angle. We also found the stability thresholds for the stable diagonal-roll and four-roll solutions, which increase with 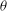$\theta $ until they disappear at other critical angles. Finally, the families of stable solutions are presented in the 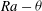$\mathit{Ra}-\theta $ parameter space by determining the locus of the primary, secondary, saddle-node, and Hopf bifurcation points as a function of 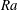$\mathit{Ra}$ and 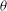$\theta $.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Convection: Convection in cavities Nonlinear Dynamical Systems: Pattern formation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 650 - 688
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adachi, T. 2006 Stability of natural convection in an inclined square duct with perfectly conducting side walls. Intl J. Heat Mass Transfer 49, 2372–2380.CrossRefGoogle Scholar
Altaç, Z. & Kurtul, Ö. 2007 Natural convection in tilted rectangular enclosures with a vertically situated hot plate inside. Appl. Therm. Engng 27, 1832–1840.Google Scholar
Baumgardner, J. R. 1985 Three-dimensional treatment of convective flow in the Earth’s mantle. J. Stat. Phys. 39, 501–511.CrossRefGoogle Scholar
Beaume, C., Bergeon, A. & Knobloch, E. 2013 Convectons and secondary snaking in three-dimensional natural doubly diffusive convection. Phys. Fluids 25, 024105.Google Scholar
Bénard, H. 1901 Les tourbillons cellulaires dans une nappe liquide. – Méthodes optiques d’observation et d’enregistrement. J. Phys. Theor. Appl. 10, 254–266.Google Scholar
Ben Hadid, H. & Henry, D. 1997 Numerical study of convection in the horizontal Bridgman configuration under the action of a constant magnetic field. Part 2: three-dimensional flow. J. Fluid Mech. 333, 57–83.Google Scholar
Bergeon, A., Ghorayeb, K. & Mojtabi, A. 1999 Double diffusive instability in an inclined cavity. Phys. Fluids 11, 549–559.Google Scholar
Bergeon, A., Henry, D., Ben Hadid, H. & Tuckerman, L. S. 1998 Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 375, 143–177.Google Scholar
Bergeon, A., Henry, D. & Knobloch, E. 2001 Three-dimensional Marangoni–Bénard flows in square and nearly square containers. Phys. Fluids 13, 92–98.Google Scholar
Bergeon, A. & Knobloch, E. 2002 Natural doubly diffusive convection in three-dimensional enclosures. Phys. Fluids 14, 3233–3250.CrossRefGoogle Scholar
Borońska, K. & Tuckerman, L. S. 2010 Extreme multiplicity in cylindrical Rayleigh–Bénard convection. II. Bifurcation diagram and symmetry classification. Phys. Rev. E 81, 036321.Google Scholar
Catton, I. 1972 The effect of insulating vertical walls on the onset of motion in a fluid heated from below. Intl J. Heat Mass Transfer 15, 665–672.CrossRefGoogle Scholar
Cliffe, K. A. & Winters, K. H. 1984 A numerical study of the cusp catastrophe for Bénard convection in tilted cavities. J. Comput. Phys. 54, 531–534.CrossRefGoogle Scholar
Cliffe, K. A. & Winters, K. H. 1986 The use of symmetry in bifurcation calculations and its application to the Bénard problem. J. Comput. Phys. 67, 310–326.CrossRefGoogle Scholar
Emanuel, K. A. 1994 Atmospheric Convection. Oxford University Press.Google Scholar
Fusegi, T., Hyun, J. M., Kuwahara, K. & Farouk, B. 1991 A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure. Intl J. Heat Mass Transfer 34, 1543–1557.Google Scholar
Getling, A. V. 1998 Rayleigh–Bénard Convection: Structures and Dynamics. World Scientific.CrossRefGoogle Scholar
Henry, D. & Ben Hadid, H. 2007 Multiple flow transitions in a box heated from the side in low-Prandtl-number fluids. Phys. Rev. E 76, 016314.Google Scholar
Juel, A., Mullin, T., Ben Hadid, H. & Henry, D. 2001 Three-dimensional free convection in molten gallium. J. Fluid Mech. 436, 267–281.CrossRefGoogle Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting method for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Kirchartz, K. R. & Oertel, H. Jr 1988 Three-dimensional thermal cellular convection in rectangular boxes. J. Fluid Mech. 192, 249–286.CrossRefGoogle Scholar
Koutsoheras, W. & Charters, W. W. S. 1977 Natural convection phenomena in inclined cells with finite side-walls – a numerical solution. Solar Energy 19, 433–438.Google Scholar
Lappa, M. 2005 Thermal convection and related instabilities in models of crystal growth from the melt on earth and in microgravity: past history and current status. Cryst. Res. Technol. 40, 531–549.Google Scholar
Lo Jacono, D., Bergeon, A. & Knobloch, E. 2013 Three-dimensional spatially localized binary-fluid convection in a porous medium. J. Fluid Mech. 730, R2.CrossRefGoogle Scholar
Mallinson, G. D. & Davis, G. D. V. 1977 Thee-dimensional natural convection in a box: a numerical study. J. Fluid Mech. 83, 1–31.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 7, 80–91.CrossRefGoogle Scholar
Mercader, I., Batiste, O. & Alonso, A. 2010 An efficient spectral code for incompressible flows in cylindrical geometries. Comput. Fluids 39, 215–224.CrossRefGoogle Scholar
Mohamad, A. A., Sicard, J. & Bennacer, R. 2006 Natural convection in enclosures with floor cooling subjected to a heated vertical wall. Intl J. Heat Mass Transfer 49, 108–121.Google Scholar
Moya, S. L., Ramos, E. & Sen, M. 1987 Numerical study of natural convection in a tilted rectangular porous material. Intl J. Heat Mass Transfer 30, 741–756.Google Scholar
Ozoe, H., Fujii, K., Noam, L. & Churchill, S. W. 1983 Long rolls generated by natural convection in an inclined, rectangular enclosure. Intl J. Heat Mass Transfer 26, 1427–1438.Google Scholar
Ozoe, H., Sayama, H. & Churchill, S. W. 1974 Natural convection in an inclined square channel. Intl J. Heat Mass Transfer 17, 401–406.Google Scholar
Ozoe, H., Sayama, H. & Churchill, S. W. 1977 Natural convection patterns in a long inclined rectangular box heated from below: Part I. Three-directional photography. Intl J. Heat Mass Transfer 20, 123–129.Google Scholar
Pallares, J., Arroyo, M. P., Grau, F. X. & Giralt, F. 2001 Experimental laminar Rayleigh–Bénard convection in a cubical cavity at moderate Rayleigh and Prandtl numbers. Exp. Fluids 31, 208–218.Google Scholar
Petrone, G., Chénier, E. & Lauriat, G. 2004 Stability of free convection in air-filled horizontal annuli: influence of the radius ratio. Intl J. Heat Mass Transfer 47, 3889–3907.Google Scholar
Puigjaner, D., Herrero, J., Giralt, F. & Simó, C. 2004 Stability analysis of the flow in a cubical cavity heated from below. Phys. Fluids 16, 3639–3655.Google Scholar
Puigjaner, D., Herrero, J., Giralt, F. & Simó, C. 2006 Bifurcation analysis of multiple steady flow patterns for Rayleigh–Bénard convection in a cubical cavity at Pr = 130. Phys. Rev. E 73, 046304.Google Scholar
Puigjaner, D., Herrero, J., Simó, C. & Giralt, F. 2008 Bifurcation analysis of steady Rayleigh–Bénard convection in a cubical cavity with conducting sidewalls. J. Fluid Mech. 598, 393–427.CrossRefGoogle Scholar
Rayleigh, L. 1916 On convective currents in a horizontal layer of fluid when the higher temperature is on the under side. Phil. Mag. 32 (192), 529–546.Google Scholar
Seydel, R. 2009 Practical Bifurcation and Stability Analysis. Springer.Google Scholar
Torres, J. F., Henry, D., Komiya, A., Maruyama, S. & Ben Hadid, H. 2013 Three-dimensional continuation study of convection in a tilted rectangular enclosure. Phys. Rev. E 88, 043015.Google Scholar
Wakashima, S. & Saitoh, T. S. 2004 Benchmark solutions for natural convection in a cubic cavity using the high-order time–space method. Intl J. Heat Mass Transfer 47, 853–864.CrossRefGoogle Scholar