Published online by Cambridge University Press: 27 October 2021
The initial flow past an impulsively started translating circular cylinder is asymptotically analysed using a Brinkman penalization method on the Navier–Stokes equations. The asymptotic solution obtained shows that the tangential and normal slip velocities on the cylinder surface are of the order of  $1/\sqrt {\lambda }$ and
$1/\sqrt {\lambda }$ and  $1/\lambda$, respectively, within the second approximation of the present asymptotic analysis, where
$1/\lambda$, respectively, within the second approximation of the present asymptotic analysis, where  $\lambda$ is the penalization parameter. This result agrees with the estimation of Carbou & Fabrie (Adv. Diff. Equ., vol. 8, 2003, pp. 1453–1480). Based on the asymptotic solution, the influence of the penalization parameter
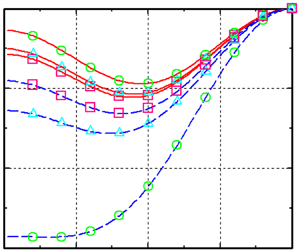
$\lambda$ is the penalization parameter. This result agrees with the estimation of Carbou & Fabrie (Adv. Diff. Equ., vol. 8, 2003, pp. 1453–1480). Based on the asymptotic solution, the influence of the penalization parameter  $\lambda$ is discussed on the drag coefficient that is calculated using the adopted three formulae. It can then be found that the drag coefficient calculated from the integration of the penalization term exhibits a half-value of the results of Bar-Lev & Yang (J. Fluid Mech., vol. 72, 1975, pp. 625–647) as
$\lambda$ is discussed on the drag coefficient that is calculated using the adopted three formulae. It can then be found that the drag coefficient calculated from the integration of the penalization term exhibits a half-value of the results of Bar-Lev & Yang (J. Fluid Mech., vol. 72, 1975, pp. 625–647) as  $\lambda \to \infty$.
$\lambda \to \infty$.