Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-08T21:52:41.317Z Has data issue: false hasContentIssue false
  • English
  • Français

An invariant representation of mean inertia: theoretical basis for a log law in turbulent boundary layers

Published online by Cambridge University Press:  20 January 2017

Caleb Morrill-Winter ,
Jimmy Philip  and
Joseph Klewicki
Caleb Morrill-Winter*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Joseph Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia Mechanical Engineering Department, University of New Hampshire, Durham, NH 03824, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

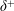A refined scaling analysis of the two-dimensional mean momentum balance (MMB) for the zero-pressure-gradient turbulent boundary layer (TBL) is presented and experimentally investigated up to high friction Reynolds numbers, $\unicode[STIX]{x1D6FF}^{+}$. For canonical boundary layers, the mean inertia, which is a function of the wall-normal distance, appears instead of the constant mean pressure gradient force in the MMB for pipes and channels. The constancy of the pressure gradient has led to theoretical treatments for pipes/channels, that are more precise than for the TBL. Elements of these analyses include the logarithmic behaviour of the mean velocity, specification of the Reynolds shear stress peak location, the square-root Reynolds number scaling for the log layer onset and a well-defined layer structure based on the balance of terms in the MMB. The present analyses evidence that similarly well-founded results also hold for turbulent boundary layers. This follows from transforming the mean inertia term in the MMB into a form that resembles that in pipes/channels, and is constant across the outer inertial region of the TBL. The physical reasoning is that the mean inertia is primarily a large-scale outer layer contribution, the ‘shape’ of which becomes invariant of 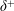$\unicode[STIX]{x1D6FF}^{+}$ with increasing 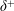$\unicode[STIX]{x1D6FF}^{+}$, and with a ‘magnitude’ that is inversely proportional to 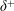$\unicode[STIX]{x1D6FF}^{+}$. The present analyses are enabled and corroborated using recent high resolution, large Reynolds number hot-wire measurements of all the terms in the TBL MMB.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 594 - 617
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Chin, C., Philip, J., Klewicki, J. C., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.CrossRefGoogle Scholar
Del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Fife, P., Klewicki, J., McMurtry, P. & Wei, T. 2005a Multiscaling in the presence of indeterminancy: wall-induced turbulence. Multiscale Model. Simul. 4, 936–959.CrossRefGoogle Scholar
Fife, P., Klewicki, J. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. A 24, 781–807.CrossRefGoogle Scholar
Fife, P., Wei, T., Klewicki, J. & McMurtry, P. 2005b Stress gradient balance layers and scale hierarchies in wall-bounded turbulent flows. J. Fluid Mech. 532, 165–189.CrossRefGoogle Scholar
Furuichi, N., Terao, Y., Wada, Y. & Tsuji, Y. 2015 Friction factor and mean velocity profile for pipe flow at high Reynolds numbers. Phys. Fluids 27 (9), 095108.CrossRefGoogle Scholar
George, W. K. 2007 Is there a universal log law for turbulent wall-bounded flows? Phil. Trans. R. Soc. Lond. A 365, 789–806.Google Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.CrossRefGoogle Scholar
Jones, M. B., Nickels, T. B. & Marusic, I. 2008 On the asymptotic similiarity of the zero-pressure gradient turbulent boundary layer. J. Fluid Mech. 616, 195–203.CrossRefGoogle Scholar
Klewicki, J. & Oberlack, M. 2015 Finite Reynolds number properties of a turbulent channel flow similarity solution. Phys. Fluids 27 (9), 095110.CrossRefGoogle Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME J. Fluids Engng 132 (9), 094001.CrossRefGoogle Scholar
Klewicki, J. C. 2013a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.CrossRefGoogle Scholar
Klewicki, J. C. 2013b Self–similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.CrossRefGoogle Scholar
Klewicki, J. C., Fife, P. & Wei, T. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. Math. Phys. Engng Sci. 365, 823–839.Google ScholarPubMed
Klewicki, J. C., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.CrossRefGoogle Scholar
Klewicki, J. C., Philip, J., Marusic, I., Chauhan, K. & Morrill-Winter, C. 2014 Self-similarity in the inertial region of wall turbulence. Phys. Rev. E 90 (6), 063015.Google ScholarPubMed
Lighthill, M. J. 1958 On displacement thickness. J. Fluid Mech. 4 (04), 383–392.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat–plate boundary layers. Phys. Fluids 15 (8), 2461–2464.CrossRefGoogle Scholar
Marusic, I., Monty, J., Hultmark, M. & Smits, A. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mellor, G. L. 1972 The large Reynolds number, asymptotic theory of turbulent boundary layers. Intl J. Engng Sci. 10 (10), 851–873.CrossRefGoogle Scholar
Metzger, M., Lyons, A. & Fife, P. 2008 Mean momentum balance in moderately favourable pressure gradient turbulent boundary layers. J. Fluid Mech. 617, 107–140.CrossRefGoogle Scholar
Millikan, C. 1939 A critical discussion of turbulent flow in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechancs. Wiley.Google Scholar
Morrill-Winter, C., Klewicki, J., Baidya, R. & Marusic, I. 2015 Temporally optimized spanwise vorticity sensor measurements in turbulent boundary layers. Exp. Fluids 56 (12), 1–14.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.Google ScholarPubMed
Panton, R. L. 2005 Review of wall turbulence as described by composite expansions. Appl. Mech. Rev. 58, 1–36.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanisms of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.CrossRefGoogle Scholar
Talluru, K. M., Djenidi, L., Kamruzzaman, M. & Antonia, R. A. 2016 Self-preservation in a zero pressure gradient rough-wall turbulent boundary layer. J. Fluid Mech. 788, 57–69.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vincenti, P., Klewicki, J. C., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54 (12), 1–13.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar