Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T16:44:47.972Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolute instabilities in eccentric Taylor–Couette–Poiseuille flow

Published online by Cambridge University Press:  17 February 2014

Colin Leclercq Open the ORCID record for Colin Leclercq [Opens in a new window] ,
Benoît Pier  and
Julian F. Scott
Colin Leclercq*
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
Benoît Pier
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
Julian F. Scott
Affiliation:
Laboratoire de mécanique des fluides et d’acoustique, École centrale de Lyon – CNRS – Université Claude-Bernard Lyon 1 – INSA Lyon, 36 avenue Guy-de-Collongue, 69134 Écully CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of eccentricity on absolute instabilities (AI) in the Taylor–Couette system with pressure-driven axial flow and fixed outer cylinder is investigated. Five modes of instability are considered, characterized by a pseudo-angular order 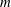$m$, with here 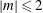$\vert m\vert \leq 2$. These modes correspond to toroidal (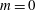$m=0$) and helical structures (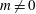$m\neq 0$) deformed by the eccentricity. Throughout the parameter range, the mode with the largest absolute growth rate is always the Taylor-like vortex flow corresponding to $m=0$. Axial advection, characterized by a Reynolds number 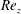${\mathit{Re}_z}$, carries perturbations downstream, and has a strong stabilizing effect on AI. On the other hand, the effect of the eccentricity $e$ is complex: increasing $e$ generally delays AI, except for a range of moderate eccentricites 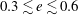${0.3\lesssim e \lesssim 0.6}$, where it favours AI for large enough 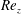${\mathit{Re}_z}$. This striking behaviour is in contrast with temporal instability, always inhibited by eccentricity, and where left-handed helical modes of increasing 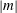$\vert m\vert $ dominate for larger 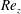${\mathit{Re}_z}$. The instability mechanism of AI is clearly centrifugal, even for the larger values of 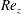${\mathit{Re}_z}$ considered, as indicated by an energy analysis. For large enough 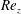${\mathit{Re}_z}$, critical modes localize in the wide gap for low $e$, but their energy distribution is shifted towards the diverging section of the annulus for moderate $e$. For highly eccentric geometries, AI are controlled by the minimal annular clearance, and the critical modes are confined to the vicinity of the inner cylinder. Untangling the AI properties of each 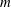$m$ requires consideration of multiple pinch points.

JFM classification

Instability: Absolute/convective instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 543 - 566
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

éeferences

Altmeyer, S., Hoffmann, C. & Lücke, M. 2011 Islands of instability for growth of spiral vortices in the Taylor–Couette system with and without axial through flow. Phys. Rev. E 84, 046308.Google Scholar
Babcock, K. L., Ahlers, G. & Cannell, D. S. 1991 Noise-sustained structure in Taylor–Couette flow with through flow. Phys. Rev. Lett. 67, 3388–3391.CrossRefGoogle ScholarPubMed
Babcock, K. L., Ahlers, G. & Cannell, D. S. 1994 Noise amplification in open Taylor–Couette flow. Phys. Rev. E 50, 3670–3692.Google Scholar
Babcock, K. L., Cannell, D. S. & Ahlers, G. 1992 Stability and noise in Taylor–Couette flow with through-flow. Physica D 61, 40–46.Google Scholar
Bers, A. 1983 Space-time evolution of plasma instabilities–absolute and convective. In Handbook of Plasma Physics (ed. Rosenbluth, M. & Sagdeev, R.), pp. 451–517. North-Holland.Google Scholar
Briggs, R. J. 1964 Electron-stream Interactions with Plasmas, pp. 1–46. MIT Press.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Coney, J. E. R. 1971 Taylor vortex flow with special reference to rotary heat exchangers. PhD thesis, Leeds University.Google Scholar
Coney, J. E. R. & Atkinson, J. 1978 The effect of Taylor vortex flow on the radial forces in an annulus having variable eccentricity and axial flow. Trans. ASME: J. Fluids Engng 100, 210–214.Google Scholar
Coney, J. E. R. & Mobbs, F. R. 1969–70 Hydrodynamic stability of the flow between eccentric rotating cylinders with axial flow: visual observations (paper 2). Proc. Inst. Mech. Engrs Pt 3L 184, 10–17.Google Scholar
Couette, M. 1888a La viscosité des liquides. Bull. Sci. Phys. 4, 40–62 123–133, 262–278.Google Scholar
Couette, M. 1888b Sur un nouvel appareil pour l’étude du frottement des fluides. C. R. Acad. Sci. Paris 107, 388–390.Google Scholar
Davies, J. A. 1989 Conditions for absolute instability in the cyclotron resonance maser. Phys. Fluids B 1, 663–669.Google Scholar
DiPrima, R. C. 1960 The stability of a viscous fluid between rotating cylinders with an axial flow. J. Fluid Mech. 9, 621–631.Google Scholar
DiPrima, R. C. 1963 A note on the stability of flow in loaded journal bearings. Trans. Am. Soc. Lubric. Engrs 6, 249–253.Google Scholar
DiPrima, R. C. & Stuart, J. T. 1972 Non-local effects in the stability of flow between eccentric rotating cylinders. J. Fluid Mech. 54, 393–415.Google Scholar
DiPrima, R. C. & Stuart, J. T. 1975 The nonlinear calculation of Taylor vortex flow between eccentric rotating cylinders. J. Fluid Mech. 67, 85–111.Google Scholar
DiPrima, R. C. & Swinney, H. L. 1985 Instabilities and transition in flow between concentric rotating cylinders. In Hydrodynamic Instabilities and the Transition to Turbulence (ed. Swinney, H. L. & Gollub, J. P.), pp. 139–180. Springer.Google Scholar
Eagles, P. M., Stuart, J. T. & DiPrima, R. C. 1978 The effects of eccentricity on torque and load in Taylor-vortex flow. J. Fluid Mech. 87, 209–231.Google Scholar
Escudier, M. P., Oliveira, P. J. & Pinho, F. T. 2002 Fully developed laminar flow of purely viscous non-Newtonian liquids through annuli, including the effects of eccentricity and inner-cylinder rotation. Intl J. Heat Fluid Flow 23, 52–73.Google Scholar
Guo, B. & Liu, G. 2011 Applied Drilling Circulation Systems – Hydraulics, Calculations, Models. Elsevier.Google Scholar
Healey, J. J. 2004 On the relation between the viscous and inviscid absolute instabilities of the rotating-disk boundary layer. J. Fluid Mech. 511, 179–199.CrossRefGoogle Scholar
Huerre, P. 2000 Open shear flow instabilities. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffat, H. K. & Worster, M. G.), pp. 159–229. Cambridge University Press.Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid. Mech. 22, 473–537.CrossRefGoogle Scholar
Juniper, M. P. 2006 The effect of confinement on the stability of two-dimensional shear flows. J. Fluid Mech. 565, 171–195.Google Scholar
Keller, H. B. 1977 Numerical solution of bifurcation and nonlinear eigenvalue problems. In Applications of Bifurcation Theory (ed. Rabinowitz, P.), pp. 359–384. Academic.Google Scholar
Leclercq, C., Pier, B. & Scott, J. F. 2013 Temporal stability of eccentric Taylor–Couette–Poiseuille flow. J. Fluid Mech. 733, 68–99.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1997 ARPACK Users’ Guide: Solution of Large-scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods.Google Scholar
Lücke, M. & Recktenwald, A. 1993 Amplification of molecular fluctuations into macroscopic vortices by convective instabilities. Europhys. Lett. 22, 559–564.Google Scholar
Mallock, A. 1888 Determination of the viscosity of water. Proc. R. Soc. Lond. 45, 126–132.Google Scholar
Martinand, D., Serre, E. & Lueptow, R. M. 2009 Absolute and convective instability of cylindrical Couette flow with axial and radial flows. Phys. Fluids 21, 104102.Google Scholar
Mobbs, F. R. & Younes, M. A. M. A. 1974 The Taylor vortex regime in the flow between eccentric rotating cylinders. Trans. ASME: J. Lubric. Tech. 127–134.Google Scholar
Ng, B. S. & Turner, E. R. 1982 On the linear stability of spiral flow between rotating cylinders. Proc. R. Soc. Lond. A 382, 83–102.Google Scholar
Pier, B. & Huerre, P. 1996 Fully nonlinear global modes in spatially developing media. Physica D 97, 206–222.Google Scholar
Pier, B. & Huerre, P. 2001 Nonlinear synchronization in open flows. J. Fluids Struct. 15, 471–480.CrossRefGoogle Scholar
Pier, B., Huerre, P. & Chomaz, J.-M. 2001 Bifurcation to fully nonlinear synchronized structures in slowly varying media. Physica D 148, 49–96.Google Scholar
Pinter, A., Lücke, M. & Hoffmann, C. 2003 Spiral and Taylor vortex fronts and pulses in axial through flow. Phys. Rev. E 67, 026318.Google ScholarPubMed
Ritchie, G. S. 1968 On the stability of viscous flow between eccentric rotating cylinders. J. Fluid Mech. 32, 131–144.Google Scholar
Sep, J. 2008 Journal bearing with an intensive axial oil flow–experimental investigation. Sci. Prob. Mach. Oper. Maintenance 43, 21–29.Google Scholar
Swift, J. B., Babcock, K. L. & Hohenberg, P. C. 1994 Effects of thermal noise in Taylor–Couette flow with corotation and axial through-flow. Physica A 204, 625–649.Google Scholar
Takeuchi, D. I. & Jankowski, D. F. 1981 Numerical and experimental investigation of the stability of spiral Poiseuille flow. J. Fluid Mech. 102, 101–126.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. 223, 289–343.Google Scholar
Tsameret, A. & Steinberg, V. 1991a Convective vs. absolute instability in Couette–Taylor flow with an axial flow. Europhys. Lett. 14, 331–336.Google Scholar
Tsameret, A. & Steinberg, V. 1991b Noise-modulated propagating pattern in a convectively unstable system. Phys. Rev. Lett. 67, 3392–3395.Google Scholar
Tsameret, A. & Steinberg, V. 1994 Absolute and convective instabilities and noise-sustained structures in the Couette–Taylor system with an axial flow. Phys. Rev. E 49, 1291–1308.Google Scholar
Vohr, J. A. 1968 An experimental study of Taylor vortices and turbulence in flow between eccentric rotating cylinders. Trans. ASME: J. Lubric. Tech. 90, 285–296.Google Scholar
Younes, M. A. M. A. 1972 The hydrodynamic stability of spiral flow between eccentric rotating cylinders. PhD thesis, Leeds University.Google Scholar
Younes, M. A. M. A., Mobbs, F. R. & Coney, J. E. R. 1972 Hydrodynamic stability of the flow between eccentric rotating cylinders with axial flow: torque measurements (paper C76/72). In Tribology Convention, Institution of Mechanical Engineers pp. 14–19.Google Scholar