Published online by Cambridge University Press: 04 November 2021
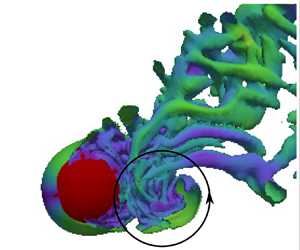
Vortex-induced vibration (VIV) of an elastically mounted sphere placed close to or piercing a free surface (FS) was investigated numerically. The submergence depth ( $h$) was systematically varied between
$h$) was systematically varied between  $1$ and
$1$ and  $-$0.75 sphere diameters (
$-$0.75 sphere diameters ( $D$) and the response simulated over the reduced velocity range
$D$) and the response simulated over the reduced velocity range  $U^*\in [3.5,14]$. The incompressible flow was coupled with the sphere motion modelled by a spring–mass–damper system, treating the free-surface boundary as a slip wall. In line with the previous experimental findings, as the submergence depth was decreased from
$U^*\in [3.5,14]$. The incompressible flow was coupled with the sphere motion modelled by a spring–mass–damper system, treating the free-surface boundary as a slip wall. In line with the previous experimental findings, as the submergence depth was decreased from  $h^* = h/D =1$, the maximum response amplitude of the fully submerged sphere decreased; however, as the sphere pierced the FS, the amplitude increased until
$h^* = h/D =1$, the maximum response amplitude of the fully submerged sphere decreased; however, as the sphere pierced the FS, the amplitude increased until  $h^* = -0.375$, and then decreased beyond that point. The fluctuating components of the lift and drag coefficients also followed the same pattern. The variation of the near-wake vortex dynamics over this submergence range was examined in detail to understand the effects of
$h^* = -0.375$, and then decreased beyond that point. The fluctuating components of the lift and drag coefficients also followed the same pattern. The variation of the near-wake vortex dynamics over this submergence range was examined in detail to understand the effects of  $h^*$ on the VIV response. It was found that
$h^*$ on the VIV response. It was found that  $h^* = 1$ is a critical submergence depth, beyond which, as
$h^* = 1$ is a critical submergence depth, beyond which, as  $h^*$ is decreased, the vortical structures in the wake vary significantly. For a fully submerged sphere, the influence of the stress-free condition on the VIV response was dominant over the kinematic constraint preventing flow through the surface. For piercing sphere cases, two previously unseen vortical recirculations were formed behind the sphere near times of maximal displacement, enhancing the VIV response. These were strongest at
$h^*$ is decreased, the vortical structures in the wake vary significantly. For a fully submerged sphere, the influence of the stress-free condition on the VIV response was dominant over the kinematic constraint preventing flow through the surface. For piercing sphere cases, two previously unseen vortical recirculations were formed behind the sphere near times of maximal displacement, enhancing the VIV response. These were strongest at  $h^* = -0.375$, and much weaker for small submergence depths, explaining the observed response-amplitude variation.
$h^* = -0.375$, and much weaker for small submergence depths, explaining the observed response-amplitude variation.