Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T02:35:48.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex dynamics for flow over a circular cylinder in proximity to a wall

Published online by Cambridge University Press:  05 January 2017

Guo-Sheng He ,
Jin-Jun Wang ,
Chong Pan ,
Li-Hao Feng ,
Qi Gao  and
Akira Rinoshika
Guo-Sheng He
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
Jin-Jun Wang*
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
Chong Pan
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
Li-Hao Feng
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
Qi Gao
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
Akira Rinoshika
Affiliation:
Ministry of Education Key Laboratory of Fluid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of vortical structures in flow over a circular cylinder in the vicinity of a flat plate is investigated using particle image velocimetry (PIV). The cylinder is placed above the flat plate with its axis parallel to the wall and normal to the flow direction. The Reynolds number $Re_{D}$ based on the cylinder diameter 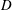$D$ is 1072 and the gap 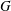$G$ between the cylinder and the flat plate is varied from gap-to-diameter ratio 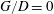$G/D=0$ to 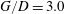$G/D=3.0$. The flow statistics and vortex dynamics are strongly dependent on the gap ratio 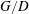$G/D$. Statistics show that as the cylinder comes close to the wall (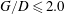$G/D\leqslant 2.0$), the cylinder wake becomes more and more asymmetric and a boundary layer separation is induced on the flat plate downstream of the cylinder. The wake vortex shedding frequency increases with decreasing 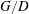$G/D$ until a critical gap ratio (about 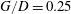$G/D=0.25$) below which the vortex shedding is irregular. The deflection of the gap flow away from the wall and its following interaction with the upper shear layer may be the cause of the higher shedding frequency. The vortex dynamics is investigated based on the phase-averaged flow field and virtual dye visualization in the instantaneous PIV velocity field. It is revealed that when the cylinder is close to the wall (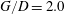$G/D=2.0$), the cylinder wake vortices can periodically induce secondary spanwise vortices near the wall. As the cylinder approaches the wall (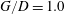$G/D=1.0$) the secondary vortex can directly interact with the lower wake vortex, and a further approaching of the cylinder (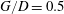$G/D=0.5$) can result in more complex interactions among the secondary vortex, the lower wake vortex and the upper wake vortex. The breakdown of vortices into filamentary debris during vortex interactions is clearly revealed by the coloured virtual dye visualizations. For 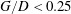$G/D<0.25$, the lower shear layer is strongly inhibited and only the upper shear layer can shed vortices. Investigation of the vortex formation, evolution and interaction in the flow promotes the understanding of the flow physics for different gap ratios.

JFM classification

Boundary Layers: Boundary layer structure Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 698 - 720
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angrilli, F., Bergamaschi, S. & Cossalter, V. 1982 Investigation of wall induced modifications to vortex shedding from a circular cylinder. Trans. ASME J. Fluids Engng 104, 518–522.CrossRefGoogle Scholar
Bearman, P. W. & Zdravkovich, M. M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89, 33–47.CrossRefGoogle Scholar
Dipankar, A. & Sengupta, T. K. 2005 Flow past a circular cylinder in the vicinity of a plane wall. J. Fluids Struct. 20 (3), 403–423.Google Scholar
Doligalski, T. L. 1994 Vortex interactions with walls. Annu. Rev. Fluid Mech. 26, 573–616.Google Scholar
Dritschel, D. G. 1995 A general theory for two-dimensional vortex interactions.. J. Fluid Mech. 293, 269–303.CrossRefGoogle Scholar
He, G. S., Pan, C., Feng, L. H., Gao, Q. & Wang, J. J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.Google Scholar
He, G. S. & Wang, J. J. 2013 Dynamics of vortical structures in cylinder–wall interaction with moderate gap ratio. J. Fluids Struct. 43, 100–109.Google Scholar
He, G. S., Wang, J. J. & Pan, C. 2013 Initial growth of a disturbance in a boundary layer influenced by a circular cylinder wake. J. Fluid Mech. 718, 116–130.Google Scholar
Jensen, A., Pedersen, G. K. & Wood, D. J. 2003 An experimental study of wave run-up at a steep beach. J. Fluid Mech. 486, 161–188.CrossRefGoogle Scholar
Küchemann, D. 1965 Report on the I.U.T.A.M. symposium on concentrated vortex motions in fluids. J. Fluid Mech. 21, 1–20.CrossRefGoogle Scholar
Lei, C., Cheng, L. & Kavanagh, K. 1999 Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder. J. Wind Engng Ind. Aerodyn. 80, 263–286.Google Scholar
Liu, X. & Katz, J. 2006 Instantaneous pressure and material acceleration measurements using a four-exposure PIV system. Exp. Fluids 41, 227–240.Google Scholar
Mandal, A. C. & Dey, J. 2011 An experimental study of boundary layer transition induced by a cylinder wake. J. Fluid Mech. 684, 60–84.Google Scholar
Moore, D. W. & Saifman, P. G. 1975 The density of organized vortices in a turbulent mixing layer. J. Fluid Mech. 69, 465–473.Google Scholar
Pan, C., Wang, J. J., Zhang, P. F. & Feng, L. H. 2008 Coherent structures in bypass transition induced by a cylinder wake. J. Fluid Mech. 603, 367–389.Google Scholar
Price, S. J., Sumner, D., Smith, J. G., Leong, K. & Paidoussis, M. P. 2002 Flow visualization around a circular cylinder near to a plane wall. J. Fluids Struct. 16 (2), 175–191.CrossRefGoogle Scholar
Roshko, A. 1976 Structure of turbulent shear flows: a new look. AIAA J. 14, 1349–1357.Google Scholar
Saffman, P. G. 1981 Dynamics of vorticity. J. Fluid Mech. 106, 49–58.Google Scholar
Saffman, P. G. & Baker, G. R. 1979 Vortex interactions. Annu. Rev. Fluid Mech. 11, 95–122.CrossRefGoogle Scholar
Sarkar, S. & Sarkar, S. 2009 Large-eddy simulation of wake and boundary layer interactions behind a circular cylinder. Trans. ASME J. Fluids Engng 131 (9), 091201.CrossRefGoogle Scholar
Sarkar, S. & Sarkar, S. 2010 Vortex dynamics of a cylinder wake in proximity to a wall. J. Fluids Struct. 26 (1), 19–40.CrossRefGoogle Scholar
Sengupta, T. K., De, S. & Sarkar, S. 2003 Vortex-induced instability of an incompressible wall-bounded shear layer. J. Fluid Mech. 493, 277–286.Google Scholar
Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105.Google Scholar
Shadden, S. C., Katija, K., Rosenfeld, M., Marsden, J. E. & Dabiri, J. O. 2007 Transport and stirring induced by vortex formation. J. Fluid Mech. 593, 315–331.CrossRefGoogle Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10, 2281.Google Scholar
Squire, L. C. 1989 Interactions between wakes and boundary-layers. Prog. Aerosp. Sci. 26, 261–288.Google Scholar
Taniguchi, S. & Miyakoshi, K. 1990 Fluctuating fluid forces acting on a circular cylinder and interference with a plane wall. Exp. Fluids 9, 197–204.CrossRefGoogle Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. The Parabolic Press.Google Scholar
Wang, X. K. & Tan, S. K. 2008 Near-wake flow characteristics of a circular cylinder close to a wall. J. Fluids Struct. 24 (5), 605–627.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: a mechanism of turbulent mixing layer growth at moderate Reynolds number. J. Fluid Mech. 63, 237–255.Google Scholar
Zdravkovich, M. M. 1985 Forces on a circular cylinder near a plane wall. Appl. Ocean Res. 7, 197–201.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanism for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar

He supplementary movie

Movie 1 for Figure 8: Phase-averaged vortical structures at G/D=0.5.

Download He supplementary movie(Video)
Video 5.6 MB

He supplementary movie

Movie 2 for Figure 9: Phase-averaged vortical structures at G/D=1.0.

Download He supplementary movie(Video)
Video 6.9 MB

He supplementary movie

Movie 3 for Figure 10: Phase-averaged vortical structures at G/D=2.0.

Download He supplementary movie(Video)
Video 4.8 MB

He supplementary movie

Movie 4 for Figure 13: Instantaneous vortical structures at G/D=0.5 revealed by virtual dye visualization.

Download He supplementary movie(Video)
Video 1.8 MB

He supplementary movie

Movie 5 for Figure 14: Instantaneous vortical structures at G/D=1.0 revealed by virtual dye visualization.

Download He supplementary movie(Video)
Video 2.9 MB

He supplementary movie

Movie 6 for Figure 15: Instantaneous vortical structures at G/D=2.0 revealed by virtual dye visualization.

Download He supplementary movie(Video)
Video 1.4 MB