Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T05:21:27.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscoelasticity and the dynamics of concentrated particle suspension in channel flow

Published online by Cambridge University Press:  27 August 2020

Amir Esteghamatian Open the ORCID record for Amir Esteghamatian [Opens in a new window]  and
Tamer A. Zaki Open the ORCID record for Tamer A. Zaki [Opens in a new window]
Amir Esteghamatian
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21218, USA
Tamer A. Zaki*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

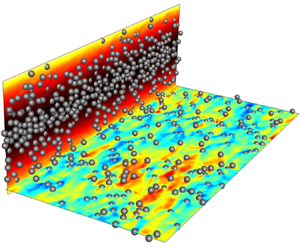
The interplay of particles and viscoelasticity in turbulent channel flow is studied using direct numerical simulations. The particle concentration is moderate at 20 % solid volume fraction, and the range of fluid elasticity spans from zero for Newtonian fluid to high Weissenberg numbers, $Wi = 25$. Qualitative changes in the flow dynamics are observed compared with dilute suspensions which were studied previously and are known to promote the cycles of hibernating and active turbulence. In contrast, at moderate concentration of particles, these cycles are entirely absent at the same level of fluid elasticity. In addition, instead of the commonly anticipated polymer drag reduction, a drag increase is observed when elasticity exceeds a threshold Weissenberg number. The higher drag is examined at various scales, starting from a global stress balance and down to the level of the particle microstructure. A key factor is the increase in polymer stresses, while the Reynolds shear stress is nearly eradicated. An explanation is provided by analysing the polymer conformation tensor using appropriate measures of its departure from the equilibrium state, with particular focus on the fluid in the vicinity of the particles. It is also demonstrated that viscoelasticity markedly affects both the diffusion and migration dynamics of the particles: diffusion is inhibited due to suppression of turbulent activity and, as a result, reduced mixing of particles and faster decorrelation of their motion; migration is preferential towards the channel centre, which leads to appreciable clustering in that region, which has a direct impact on the local polymer stresses.

JFM classification

Non-Newtonian Flows: Polymers Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A25
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agarwal, A., Brandt, L. & Zaki, T. A. 2014 Linear and nonlinear evolution of a localized disturbance in polymeric channel flow. J. Fluid Mech. 760, 278–303.CrossRefGoogle Scholar
Becker, L. E., McKinley, G. H., Rasmussen, H. K. & Hassager, O. 1994 The unsteady motion of a sphere in a viscoelastic fluid. J. Rheol. 38 (2), 377–403.CrossRefGoogle Scholar
Chhabra, R. P. 2006 Bubbles, Drops, and Particles in non-Newtonian Fluids. CRC.CrossRefGoogle Scholar
Choueiri, G. H., Lopez, J. M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120 (12), 124501.CrossRefGoogle ScholarPubMed
Costa, P., Picano, F., Brandt, L. & Breugem, W. P. 2018 Effects of the finite particle size in turbulent wall-bounded flows of dense suspensions. J. Fluid Mech. 843, 450–478.CrossRefGoogle Scholar
Dai, S. & Tanner, R. I. 2017 Elongational flows of some non-colloidal suspensions. Rheol. Acta 56 (1), 63–71.CrossRefGoogle Scholar
D'Avino, G., Greco, F. & Maffettone, P. L. 2017 Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 49 (1), 341–360.CrossRefGoogle Scholar
D'Avino, G. & Maffettone, P. L. 2015 Particle dynamics in viscoelastic liquids. J. Non-Newtonian Fluid Mech. 215, 80–104.CrossRefGoogle Scholar
Denn, M. M. & Morris, J. F. 2014 Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Engng 5, 203–228.CrossRefGoogle ScholarPubMed
Draad, A. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1998 Laminar–turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J. Fluid Mech. 377, 267–312.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V. E., White, C. M., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74 (4), 311–329.CrossRefGoogle Scholar
Einarsson, J., Yang, M. & Shaqfeh, E. S. G. 2018 Einstein viscosity with fluid elasticity. Phys. Rev. Fluids 3 (1), 013301.CrossRefGoogle Scholar
Esteghamatian, A. & Zaki, T. A. 2019 Dilute suspension of neutrally buoyant particles in viscoelastic turbulent channel flow. J. Fluid Mech. 875, 286–320.CrossRefGoogle Scholar
Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D. & Périaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
Goyal, N. & Derksen, J. J. 2012 Direct simulations of spherical particles sedimenting in viscoelastic fluids. J. Non-Newtonian Fluid Mech. 183–184, 1–13.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2000 Elastic turbulence in a polymer solution flow. Nature 405 (6782), 53–55.CrossRefGoogle Scholar
Hameduddin, I., Gayme, D. F. & Zaki, T. A. 2019 Perturbative expansions of the conformation tensor in viscoelastic flows. J. Fluid Mech. 858, 377–406.CrossRefGoogle Scholar
Hameduddin, I., Meneveau, C., Zaki, T. A. & Gayme, D. F. 2018 Geometric decomposition of the conformation tensor in viscoelastic turbulence. J. Fluid Mech. 842, 395–427.CrossRefGoogle Scholar
Hameduddin, I. & Zaki, T. A. 2019 The mean conformation tensor in viscoelastic turbulence. J. Fluid Mech. 865, 363–380.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 2012 Low Reynolds Number Hydrodynamics: with Special Applications to Particulate Media, Vol. 1. Springer Science & Business Media.Google Scholar
Hwang, W. R., Hulsen, M. A. & Meijer, H. E. H. 2004 Direct simulations of particle suspensions in a viscoelastic fluid in sliding bi-periodic frames. J. Non-Newtonian Fluid Mech. 121 (1), 15–33.CrossRefGoogle Scholar
Jeffrey, D. J. & Acrivos, A. 1976 The rheological properties of suspensions of rigid particles. AIChE J. 22 (3), 417–432.CrossRefGoogle Scholar
Karnis, A. & Mason, S. G. 1966 Particle motions in sheared suspensions. XIX. Viscoelastic media. Trans. Soc. Rheol. 10 (2), 571–592.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newtonian Fluid Mech. 138 (2–3), 87–97.CrossRefGoogle Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20 (4), 040602.CrossRefGoogle Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.CrossRefGoogle Scholar
Lee, S. J. & Zaki, T. A. 2017 Simulations of natural transition in viscoelastic channel flow. J. Fluid Mech. 820, 232–262.CrossRefGoogle Scholar
Leshansky, A. M., Bransky, A., Korin, N. & Dinnar, U. 2007 Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys. Rev. Lett. 98 (23), 234501.CrossRefGoogle Scholar
Li, G., McKinley, G. H. & Ardekani, A. M. 2015 Dynamics of particle migration in channel flow of viscoelastic fluids. J. Fluid Mech. 785, 486–505.CrossRefGoogle Scholar
De Lillo, F., Boffetta, G. & Musacchio, S. 2012 Control of particle clustering in turbulence by polymer additives. Phys. Rev. E 85 (3), 1–6.CrossRefGoogle ScholarPubMed
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys. Fluids 25 (12), 123304.CrossRefGoogle Scholar
Matas, J.-P, Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 014501.CrossRefGoogle ScholarPubMed
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.CrossRefGoogle Scholar
Nicolaou, L., Jung, S. Y. & Zaki, T. A. 2015 A robust direct-forcing immersed boundary method with enhanced stability for moving body problems in curvilinear coordinates. Comput. Fluids 119, 101–114.CrossRefGoogle Scholar
Nowbahar, A., Sardina, G., Picano, F. & Brandt, L. 2013 Turbophoresis attenuation in a turbulent channel flow with polymer additives. J. Fluid Mech. 732, 706–719.CrossRefGoogle Scholar
Page, J. & Zaki, T. A. 2014 Streak evolution in viscoelastic Couette flow. J. Fluid Mech. 742, 520–521.CrossRefGoogle Scholar
Page, J. & Zaki, T. A. 2015 The dynamics of spanwise vorticity perturbations in homogeneous viscoelastic shear flow. J. Fluid Mech. 777, 327–363.CrossRefGoogle Scholar
Page, J. & Zaki, T. A. 2016 Viscoelastic shear flow over a wavy surface. J. Fluid. Mech. 801, 392–429.CrossRefGoogle Scholar
Picano, F., Breugem, W. P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P, Mitra, D. & Brandt, L. 2013 Shear thickening in non-Brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111 (9), 098302.CrossRefGoogle Scholar
Rahmani, M., Hammouti, A. & Wachs, A. 2018 Momentum balance and stresses in a suspension of spherical particles in a plane Couette flow. Phys. Fluids 30 (4), 043301.CrossRefGoogle Scholar
Rosenfeld, M., Kwak, D. & Vinokur, M. 1991 A fractional step solution method for the unsteady incompressible Navier–Stokes equations in generalized coordinate systems. J. Comput. Phys. 94 (1), 102–137.CrossRefGoogle Scholar
Rueda, M. M., Auscher, M.-C., Fulchiron, R., Perie, T., Martin, G., Sonntag, P. & Cassagnau, P. 2017 Rheology and applications of highly filled polymers: a review of current understanding. Prog. Polym. Sci. 66, 22–53.CrossRefGoogle Scholar
Samanta, D., Dubief, Y., Holzner, M., Schäfer, C., Morozov, A. N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110 (26), 10557–10562.CrossRefGoogle ScholarPubMed
Scirocco, R., Vermant, J. & Mewis, J. 2005 Shear thickening in filled Boger fluids. J. Rheol. 49 (2), 551–567.CrossRefGoogle Scholar
Shao, X., Wu, T. & Yu, Z. 2012 Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. J. Fluid Mech. 693, 319–344.CrossRefGoogle Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Tanner, R. I. 2019 Rheology of noncolloidal suspensions with non-Newtonian matrices. J. Rheol. 63 (4), 705–717.CrossRefGoogle Scholar
Toms, B. A. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the 1st International Congress on Rheology, pp. 135–141. North-Holland.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.CrossRefGoogle Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40 (1), 235–256.CrossRefGoogle Scholar
Xi, L. & Graham, M. D. 2010 Active and hibernating turbulence in minimal channel flow of Newtonian and polymeric fluids. Phys. Rev. Lett. 104, 218–301.CrossRefGoogle ScholarPubMed
Yang, M. & Shaqfeh, E. S. G. 2018 a Mechanism of shear thickening in suspensions of rigid spheres in Boger fluids. Part I: dilute suspensions. J. Rheol. 62 (6), 1363–1377.CrossRefGoogle Scholar
Yang, M. & Shaqfeh, E. S. G. 2018 b Mechanism of shear thickening in suspensions of rigid spheres in Boger fluids. Part II: suspensions at finite concentration. J. Rheol. 62 (6), 1379–1396.CrossRefGoogle Scholar
Zade, S., Lundell, F. & Brandt, L. 2019 Turbulence modulation by finite-size spherical particles in Newtonian and viscoelastic fluids. Intl J. Multiphase Flow 112, 116–129.CrossRefGoogle Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2001 Normal stresses and free surface deformation in concentrated suspensions of noncolloidal spheres in a viscoelastic fluid. J. Rheol. 45 (5), 1065–1084.CrossRefGoogle Scholar