Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T14:26:38.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Rayleigh–Bénard convection in an annular cell

Published online by Cambridge University Press:  29 April 2019

Xu Zhu ,
Lin-Feng Jiang ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]  and
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]
Xu Zhu
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Lin-Feng Jiang
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
Quan Zhou*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Chao Sun*
Affiliation:
Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report an experimental study of turbulent Rayleigh–Bénard (RB) convection in an annular cell of water (Prandtl number 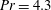$Pr=4.3$) with a radius ratio 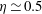$\unicode[STIX]{x1D702}\simeq 0.5$. Global quantities, such as the Nusselt number 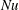$Nu$ and the Reynolds number 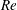$Re$, and local temperatures were measured over the Rayleigh range 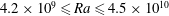$4.2\times 10^{9}\leqslant Ra\leqslant 4.5\times 10^{10}$. It is found that the scaling behaviours of 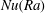$Nu(Ra)$, $Re(Ra)$ and the temperature fluctuations remain the same as those in the traditional cylindrical cells; both the global and local properties of turbulent RB convection are insensitive to the change of cell geometry. A visualization study, as well as local temperature measurements, shows that in spite of the lack of the cylindrical core, there also exists a large-scale circulation (LSC) in the annular system: thermal plumes organize themselves with the ascending hot plumes on one side and the descending cold plumes on the opposite side. Near the upper and lower plates, the mean flow moves along the two circular branches. Our results further reveal that the dynamics of the LSC in this annular geometry is different from that in the traditional cylindrical cell, i.e. the orientation of the LSC oscillates in a narrow azimuthal angle range, and no cessations, reversals or net rotation were detected.

JFM classification

Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , R5
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Araujo, F. F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084502.Google Scholar
Bao, Y., Chen, J., Liu, B.-F., She, Z.-S., Zhang, J. & Zhou, Q. 2015 Enhanced heat transport in partitioned thermal convection. J. Fluid Mech. 784, R5.Google Scholar
Benzi, R. & Verzicco, R. 2008 Numerical simulations of flow reversal in Rayleigh–Bénard convection. Europhys. Lett. 81, 64008.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.Google Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 10, 10005.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Castaing, B., Gnuaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard turbulent convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.Google Scholar
Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulence Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.Google Scholar
Chillà, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Eur. Phys. J. B 40, 223–227.Google Scholar
Chilla, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container? Phys. Rev. Lett. 87, 184501.Google Scholar
Du, Y.-B. & Tong, P. 2001 Temperature fluctuations in a convection cell with rough upper and lower surfaces. Phys. Rev. E 63, 046303.Google Scholar
Foroozani, N., Niemela, J. J., Armenio, V. & Sreenivasan, K. R. 2017 Reorientations of the large-scale flow in turbulent convection in a cube. Phys. Rev. E 95, 033107.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
He, X.-Z., Bodenschatz, E. & Ahlers, G. 2016 Azimuthal diffusion of the large-scale-circulation plane, and absence of significant non-Boussinesq effects, in turbulent convection near the ultimate-state transition. J. Fluid Mech. 791, R3.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Huang, Y.-X. & Zhou, Q. 2013 Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 737, R3.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Mishra, P. K., De, A. K., Verma, M. K. & Eswaran, V. 2011 Dynamics of reorientaiton and reversal of large-scale-flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003 Rayleigh-number evolution of large-scale coherent motion in turbulent convection. Europhys. Lett. 62, 829–833.Google Scholar
Pandey, A., Scheel, J. D. & Schumacher, J. 2018 Turbulent superstructures in Rayleigh–Bénard convection. Nat. Commun. 9, 2118.Google Scholar
van der Poel, E. P., Stevens, J. A. M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.Google Scholar
Qiu, X.-L. & Tong, P. 2002 Temperature oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 66, 026308.Google Scholar
Song, H. & Tong, P. 2010 Scaling laws in turbulent Rayleigh–Bénard convection under different geometry. Europhys. Lett. 90, 44001.Google Scholar
Stevens, R. J. A. M., Blass, A., Zhu, X., Verzicco, R. & Lohse, D. 2018 Turbulent thermal superstructures in Rayleigh–Bénard convection. Phys. Rev. Fluid 3, 041501(R).Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2011a Effect of plumes on measuring the large scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 095110.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011b Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T.-S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005 Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.Google Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google Scholar
Sun, C. & Xia, K.-Q. 2007 Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection. J. Fluid Mech. 570, 479–489.Google Scholar
Sun, C. & Zhou, Q. 2014 Experimental techniques for turbulent Taylor–Couette flow and Rayleigh–Bénard convection. Nonlinearity 27, R89–R121.Google Scholar
Verzicco, R. 2004 Effects of nonperfect thermal sources in turbulent thermal convection. Phys. Fluids 16, 1965–1979.Google Scholar
Vogt, T., Horn, S., Grannan, A. M. & Aurnou, M. 2018 Jump rope vortex in liquid metal convection. Proc. Natl Acad. Sci. USA 12, 260115.Google Scholar
Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid Mech. 697, 336–366.Google Scholar
Wang, B.-F., Wan, Z.-H., Ma, D.-J. & Sun, D.-J. 2014 Rayleigh–Bénard convection in a vertical annular container near the convection threshold. Phys. Rev. E 89, 043014.Google Scholar
Wang, Y., Lai, P.-Y., Song, H. & P., Tong 2018 Mechanism of large-scale flow reversals in turbulent thermal convection. Sci. Adv. 4, eaat7480.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 The cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.Google Scholar
Xi, H.-D., Zhang, Y.-B., Hao, J.-T. & Xia, K.-Q. 2016 Higher-order flow modes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 805, 31–51.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q. & Lui, S.-L. 1997 Turbulent thermal convection with an obstructed sidewall. Phys. Rev. Lett. 79 (25), 5006–5009.Google Scholar
Xie, Y.-C., Ding, G.-Y. & Xia, K.-Q. 2018 Flow topology transition via global bifurcation in thermally driven turbulence. Phys. Rev. Lett. 120, 214501.Google Scholar
Xie, Y.-C., Wei, P. & Xia, K.-Q. 2013 Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection. J. Fluid Mech. 717, 322–346.Google Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bênard convection. J. Fluid Mech. 814, 165–184.Google Scholar
Zhang, Y.-Z., Sun, C., Bao, Y. & Zhou, Q. 2018 How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 836, R2.Google Scholar
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.Google Scholar
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.Google Scholar

Zhu et al. supplementary movie 1

The shadowgraph movie about the ascending plumes on one side of the annulus cell, and a schematic draw showing the large-scale circulation and the spatial distribution of thermal plumes at $Ra=4.5 imes10^{10}$. The purple frame marks the visualization window.

Download Zhu et al. supplementary movie 1(Video)
Video 9.4 MB

Zhu et al. supplementary movie 2

The shadowgraph movie about the cold plumes moving along the circular branches near the upper plate, and a schematic draw showing the large-scale circulation and the spatial distribution of thermal plumes at $Ra=4.5 imes10^{10}$. The purple frame marks the visualization window.

Download Zhu et al. supplementary movie 2(Video)
Video 10.1 MB

Zhu et al. supplementary movie 3

The shadowgraph movie about the descending plumes on the opposite side of the annulus cell, and a schematic draw showing the large-scale circulation and the spatial distribution of thermal plumes at $Ra=4.5 imes10^{10}$. The purple frame marks the visualization window.

Download Zhu et al. supplementary movie 3(Video)
Video 9.4 MB

Zhu et al. supplementary movie 4

The shadowgraph movie about the hot plumes moving along the circular branches near the lower plate, and a schematic draw showing the large-scale circulation and the spatial distribution of thermal plumes at $Ra=4.5 imes10^{10}$. The purple frame marks the visualization window.

Download Zhu et al. supplementary movie 4(Video)
Video 10.2 MB