Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T12:00:53.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent heat exchange between water and ice at an evolving ice–water interface

Published online by Cambridge University Press:  07 June 2016

Eshwan Ramudu ,
Benjamin Henry Hirsh ,
Peter Olson  and
Anand Gnanadesikan
Eshwan Ramudu*
Affiliation:
Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD 21218, USA
Benjamin Henry Hirsh
Affiliation:
Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD 21218, USA
Peter Olson
Affiliation:
Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD 21218, USA
Anand Gnanadesikan
Affiliation:
Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We conduct laboratory experiments on the time evolution of an ice layer cooled from below and subjected to a turbulent shear flow of warm water from above. Our study is motivated by observations of warm water intrusion into the ocean cavity under Antarctic ice shelves, accelerating the melting of their basal surfaces. The strength of the applied turbulent shear flow in our experiments is represented in terms of its Reynolds number 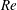$Re$, which is varied over the range 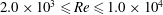$2.0\times 10^{3}\leqslant Re\leqslant 1.0\times 10^{4}$. Depending on the water temperature, partial transient melting of the ice occurs at the lower end of this range of 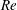$Re$ and complete transient melting of the ice occurs at the higher end. Following these episodes of transient melting, the ice reforms at a rate that is independent of 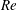$Re$. We fit our experimental measurements of ice thickness and temperature to a one-dimensional model for the evolution of the ice thickness in which the turbulent heat transfer is parameterized in terms of the friction velocity of the shear flow. Applying our model to field measurements at a site under the Antarctic Pine Island Glacier ice shelf yields a predicted melt rate that exceeds present-day observations.

JFM classification

Geophysical and Geological Flows: Ocean processes Phase change: Solidification/melting Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 572 - 597
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, H. I & Lygren, M. 2006 LES of open rotor–stator flow. Intl J. Heat Fluid Flow 27 (4), 551–557.CrossRefGoogle Scholar
Boger, D. V. & Westwater, J. W. 1967 Effect of buoyancy on the melting and freezing process. Trans. ASME J. Heat Transfer 89 (1), 81–89.Google Scholar
Brisbourne, A. M., Smith, A. M., King, E. C., Nicholls, K. W., Holland, P. R. & Makinson, K. 2014 Seabed topography beneath Larsen C Ice Shelf from seismic soundings. Cryosphere 8, 1–13.Google Scholar
Broecker, W. S., Peacock, S. L., Walker, S., Weiss, R., Fahrbach, E., Schröder, M., Mikolajewicz, U., Heinze, C., Key, R., Peng, T.-H. et al. 1998 How much deep water is formed in the Southern Ocean? J. Geophys. Res. 103 (C8), 15833–15843.Google Scholar
Cheah, S. C., Iacovides, H., Jackson, D. C., Ji, H. & Launder, B. E. 1994 Experimental investigation of enclosed rotor-stator disk flows. Exp. Therm. Fluid Sci. 9 (4), 445–455.Google Scholar
Dallaston, M. C., Hewitt, I. J. & Wells, A. J. 2015 Channelization of plumes beneath ice shelves. J. Fluid Mech. 785, 109–134.Google Scholar
Dansereau, V., Heimbach, P. & Losch, M. 2014 Simulation of subice shelf melt rates in a general circulation model: velocity-dependent transfer and the role of friction. J. Geophys. Res. Oceans 119, 1765–1790.Google Scholar
Feldmann, J. & Levermann, A. 2015 Collapse of the West Antarctic Ice Sheet after local destabilization of the Amundsen Basin. Proc. Natl Acad. Sci. USA 112, 14191–14196.Google Scholar
Galperin, B., Sukoriansky, S. & Anderson, P. S. 2007 On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Lett. 8 (3), 65–69.Google Scholar
Gilpin, R. R., Hirata, T. & Cheng, K. C. 1980 Wave formation and heat transfer at an ice–water interface in the presence of a turbulent flow. J. Fluid Mech. 99, 619–640.Google Scholar
Haynes, W. M. 2015 CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data. CRC.Google Scholar
Hellmer, H. H. & Olbers, D. J. 1989 A two-dimensional model for the thermohaline circulation under an ice shelf. Antarct. Sci. 1 (4), 325–336.Google Scholar
Holland, D. M. & Jenkins, A. 1999 Modeling thermodynamic ice-ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29 (8), 1787–1800.Google Scholar
Holland, P. R. & Feltham, D. L. 2006 The effects of rotation and ice shelf topography on frazil-laden ice shelf water plumes. J. Phys. Oceanogr. 36 (12), 2312–2327.Google Scholar
Hooke, R. L. 2005 Principles of Glacier Mechanics. Cambridge University Press.CrossRefGoogle Scholar
Huppert, H. E. & Worster, M. G. 1985 Dynamic solidification of a binary melt. Nature 314, 703–707.Google Scholar
IOC, SCOR & IAPSO 2010 The International Thermodynamic Equation of Seawater – 2010: Calculation and Use of Thermodynamic Properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English).Google Scholar
Itoh, M., Yamada, Y., Imao, S. & Gonda, M. 1992 Experiments on turbulent flow due to an enclosed rotating disk. Exp. Therm. Fluid Sci. 5 (3), 359–368.Google Scholar
Jacobs, S. S., Jenkins, A., Giulivi, C. F. & Dutrieux, P. 2011 Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf. Nat. Geosci. 4, 519–523.Google Scholar
Jenkins, A. 1991 A one-dimensional model of ice shelf-ocean interaction. J. Geophys. Res. Oceans 96 (C11), 20671–20677.Google Scholar
Jenkins, A. 2011 Convection-Driven Melting near the Grounding Lines of Ice Shelves and Tidewater Glaciers. J. Phys. Oceanogr. 41 (12), 2279–2294.Google Scholar
Jenkins, A., Dutrieux, P., Jacobs, S. S., McPhail, S. D., Perrett, J. R., Webb, A. T. & White, D. 2010a Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat. Nat. Geosci. 3, 468–472.Google Scholar
Jenkins, A., Nicholls, K. W. & Corr, H. F. J. 2010b Observation and parameterization of ablation at the base of Ronne Ice Shelf, Antarctica. J. Phys. Oceanogr. 40 (10), 2298–2312.Google Scholar
Kader, B. A. & Yaglom, A. M. 1972 Heat and mass transfer laws for fully turbulent wall flows. Intl J. Heat Mass Transfer 15, 2329–2351.Google Scholar
Kerr, R. C. & McConnochie, C. D. 2015 Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228.Google Scholar
Little, C. M., Gnanadesikan, A. & Hallberg, R. 2008 Large-scale oceanographic constraints on the distribution of melting and freezing under ice shelves. J. Phys. Oceanogr. 38 (10), 2242–2255.Google Scholar
Marinov, I., Gnanadesikan, A., Sarmiento, J. L., Toggweiler, J. R., Follows, M. & Mignone, B. K. 2008 Impact of oceanic circulation on biological carbon storage in the ocean and atmospheric pCO2. Glob. Biogeochem. Cycles 22 (3), GB3007.Google Scholar
McPhee, M. G., Maykut, G. A. & Morison, J. H. 1987 Dynamics and thermodynamics of the ice/upper ocean system in the marginal ice zone of the greenland sea. J. Geophys. Res. Oceans 92 (C7), 7017–7031.Google Scholar
Mueller, R. D., Padman, L., Dinniman, M. S., Erofeeva, S. Y., Fricker, H. A. & King, M. A. 2012 Impact of tide-topography interactions on basal melting of Larsen C Ice Shelf, Antarctica. J. Geophys. Res. Oceans 117 (C5), C05005.Google Scholar
Neufeld, J. A. & Wettlaufer, J. S. 2008 An experimental study of shear-enhanced convection in a mushy layer. J. Fluid Mech. 612, 363–385.Google Scholar
Pritchard, H. D., Ligtenberg, S. R. M., Fricker, H. A., Vaughan, D. G., Van den Broeke, M. R. & Padman, L. 2012 Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505.Google Scholar
Scheduikat, M. & Olbers, D. J. 1990 A one-dimensional mixed layer model beneath the Ross Ice Shelf with tidally induced vertical mixing. Antarc. Sci. 2 (1), 29–42.Google Scholar
Schmidtko, S., Heywood, K. J., Thompson, A. F. & Aoki, S. 2014 Multidecadal warming of Antarctic waters. Science 346, 1227–1231.Google Scholar
Stanton, T. P., Shaw, W. J., Truffer, M., Corr, H. F. J., Peters, L. E., Riverman, K. L., Bindschadler, R., Holland, D. M. & Anandakrishnan, S. 2013 Channelized ice melting in the ocean boundary layer beneath Pine Island Glacier, Antarctica. Science 341, 1236–1239.Google Scholar
Stern, A. A., Holland, D. M., Holland, P. R., Jenkins, A. & Sommeria, J. 2014 The effect of geometry on ice shelf ocean cavity ventilation: a laboratory experiment. Exp. Fluids 55 (5), 1–19.Google Scholar
Thielicke, W. & Stamhuis, E. J. 2014 PIVlab – towards user-friendly, affordable and accurate digital particle image velocimetry in matlab. J. Open Res. Software 2 (1), e30.Google Scholar
Townsend, A. A. 1964 Natural convection in water over an ice surface. Q. J. R. Meteorol. Soc. 90 (385), 248–259.Google Scholar
Tyler, S. W., Holland, D. M., Zagorodnov, V., Stern, A. A., Sladek, C., Kobs, S., White, S., Suárez, F. & Bryenton, J. 2013 Using distributed temperature sensors to monitor an Antarctic ice shelf and sub-ice-shelf cavity. J. Glaciol. 59 (215), 583–591.Google Scholar
Wagner, W. & Pruss, A. 2002 The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 31 (2), 387–535.Google Scholar
Wells, A. J. & Worster, M. G. 2011 Melting and dissolving of a vertical solid surface with laminar compositional convection. J. Fluid Mech. 687, 118–140.Google Scholar
Wettlaufer, J. S., Worster, M. G. & Huppert, H. E. 1997 Natural convection during solidification of an alloy from above with application to the evolution of sea ice. J. Fluid Mech. 344, 291–316.Google Scholar
White, F. M. 1974 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Yaglom, A. M. & Kader, B. A. 1974 Heat and mass transfer between a rough wall and turbulent fluid flow at high Reynolds and Peclet numbers. J. Fluid Mech. 62, 601–623.Google Scholar