Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T07:57:04.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient solute transport with sorption in Poiseuille flow

Published online by Cambridge University Press:  12 September 2017

Li Zhang Open the ORCID record for Li Zhang [Opens in a new window] ,
Marc A. Hesse  and
Moran Wang
Li Zhang
Affiliation:
Department of Engineering Mechanics and CNMM, Tsinghua University, Beijing, 100084, China Department of Geological Sciences, University of Texas at Austin, Austin, TX 78712, USA
Marc A. Hesse*
Affiliation:
Department of Geological Sciences, University of Texas at Austin, Austin, TX 78712, USA Institute of Computational Engineering and Sciences, University of Texas at Austin, Austin, TX 78712, USA
Moran Wang
Affiliation:
Department of Engineering Mechanics and CNMM, Tsinghua University, Beijing, 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous work on solute transport with sorption in Poiseuille flow has reached contradictory conclusions. Some have concluded that sorption increases mean solute transport velocity and decreases dispersion relative to a tracer, while others have concluded the opposite. Here we resolve this contradiction by deriving a series solution for the transient evolution that recovers previous results in the appropriate limits. This solution shows a transition in solute transport behaviour from early to late time that is captured by the first- and zeroth-order terms. 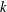Mean solute transport velocity is increased at early times and reduced at late times, while solute dispersion is initially reduced, but shows a complex dependence on the partition coefficient $k$ at late times. In the equilibrium sorption model, the time scale of the early regime and the duration of the transition to the late regime both increase with 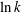$\ln k$ for large 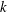$k$. The early regime is pronounced in strongly sorbing systems (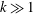$k\gg 1$). The kinetic sorption model shows a similar transition from the early to the late transport regime and recovers the equilibrium results when adsorption and desorption rates are large. As the reaction rates slow down, the duration of the early regime increases, but the changes in transport velocity and dispersion relative to a tracer diminish. In general, if the partition coefficient 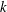$k$ is large, the early regime is well developed and the behaviour is well characterized by the analysis of the limiting case without desorption.

JFM classification

Reacting Flows: Laminar reacting flows Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 733 - 752
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, J. & Whitt, W. 2006 A unified framework for numerically inverting Laplace transforms. INFORMS J. Comput. 18 (4), 408–421.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235 (1200), 67–77.Google Scholar
Balakotaiah, V. & Chang, H. C. 1995 Dispersion of chemical solutes in chromatographs and reactors. Phil. Trans. R. Soc. Lond. A 351 (1695), 39–75.Google Scholar
Barton, N. G. 1984 An asymptotic theory for dispersion of reactive contaminants in parallel flow. J. Austral. Math. Soc. B 25, 287–310.Google Scholar
Biswas, R. R. & Sen, P. N. 2007 Taylor dispersion with absorbing boundaries: a stochastic approach. Phys. Rev. Lett. 98 (16), 164501.Google Scholar
Bolster, D., Valdés-Parada, F. J., Leborgne, T., Dentz, M. & Carrera, J. 2011 Mixing in confined stratified aquifers. J. Contam. Hydrol. 120, 198–212.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30 (1), 329–364.Google Scholar
De Gance, A. E. & Johns, L. E. 1978a On the dispersion coefficients for Poiseuille flow in a circular cylinder. Appl. Sci. Res. 34 (2–3), 227–258.Google Scholar
De Gance, A. E. & Johns, L. E. 1978b The theory of dispersion of chemically active solutes in a rectilinear flow field. Appl. Sci. Res. 34 (2–3), 189–225.Google Scholar
Dentz, M. & Carrera, J. 2007 Mixing and spreading in stratified flow. Phys. Fluids 19 (1), 017107.Google Scholar
Gill, W. N. & Sankarasubramanian, R. 1970 Exact analysis of unsteady convective diffusion. Proc. R. Soc. Lond. A 316 (1526), 341–350.Google Scholar
Golay, M. J. E. 1958 Theory of chromatography in open and coated tubular columns with round and rectangular cross-sections. In Gas Chromatography (ed. Desty, D. H.), pp. 36–53. Butterworths.Google Scholar
Haber, S. & Mauri, R. 1988 Lagrangian approach to time-dependent laminar dispersion in rectangular conduits. Part 1. Two-dimensional flows. J. Fluid Mech. 190, 201–215.Google Scholar
Hesse, F., Harms, H., Attinger, S. & Thullner, M. 2010 Linear exchange model for the description of mass transfer limited bioavailability at the pore scale. Environ. Sci. Technol. 44 (6), 2064–2071.Google Scholar
Hlushkou, D., Gritti, F., Guiochon, G., Seidel-Morgenstern, A. & Tallarek, U. 2014 Effect of adsorption on solute dispersion: a microscopic stochastic approach. Analyt. Chem. 86 (9), 4463–4470.CrossRefGoogle ScholarPubMed
Khan, M. K. 1962 Non-equilibrium theory of capillary columns and the effect of interfacial resistance on column efficiency. In Gas Chromatography (ed. Van Swaay, M.), pp. 3–17. Butterworths.Google Scholar
Latini, M. & Bernoff, A. J. 2001 Transient anomalous diffusion in Poiseuille flow. J. Fluid Mech. 441, 399–411.Google Scholar
Lungu, E. M. & Moffatt, H. K. 1982 The effect of wall conductance on heat diffusion in duct flow. J. Engng Maths 16 (2), 121–136.Google Scholar
MathWorks2012 MATLAB and Symbolic Toolbox Release 2012b. The MathWorks, Inc., Natick, MA, USA.Google Scholar
McClure, T.2013 Numerical inverse Laplace transform. Computer software. Mathworks File Exchange, Web. 1 Mar. 2016.Google Scholar
Mercer, G. N. & Roberts, A. J. 1990 A centre manifold description of contaminant dispersion in channels with varying flow properties. SIAM J. Appl. Maths 50 (6), 1547–1565.Google Scholar
Mikelić, A., Devigne, V. & van Duijn, C. J. 2006 Rigorous upscaling of the reactive flow through a pore, under dominant Peclet and Damkohler numbers. SIAM J. Math. Anal. 38 (4), 1262–1287.Google Scholar
Paine, M. A., Carbonell, R. G. & Whitaker, S. 1983 Dispersion in pulsed systems – I: heterogenous reaction and reversible adsorption in capillary tubes. Chem. Engng Sci. 38 (11), 1781–1793.Google Scholar
Sankarasubramanian, R. & Gill, W. N. 1973 Unsteady convective diffusion with interphase mass transfer. Proc. R. Soc. Lond. A 333 (1592), 115–132.Google Scholar
Shapiro, M. & Brenner, H. 1986 Taylor dispersion of chemically reactive species: irreversible first-order reactions in bulk and on boundaries. Chem. Engng Sci. 41 (6), 1417–1433.Google Scholar
Shipley, R. J. & Waters, S. L. 2012 Fluid and mass transport modelling to drive the design of cell-packed hollow fibre bioreactors for tissue engineering applications. Math. Med. Biol. 29 (4), 329–359.CrossRefGoogle ScholarPubMed
Smith, R. 1983 Effect of boundary absorption upon longitudinal dispersion in shear flows. J. Fluid Mech. 134, 161–177.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Wang, L., Cardenas, M. B., Deng, W. & Bennett, P. C. 2012 Theory for dynamic longitudinal dispersion in fractures and rivers with Poiseuille flow. Geophys. Res. Lett. 39 (5), l05401.Google Scholar
Wang, M. & Kang, Q. 2010 Modeling electrokinetic flows in microchannels using coupled lattice Boltzmann methods. J. Comput. Phys. 229 (3), 728–744.CrossRefGoogle Scholar
Wels, C., Smith, L. & Beckie, R. 1997 The influence of surface sorption on dispersion in parallel plate fractures. J. Contam. Hydrol. 28 (1–2), 95–114.CrossRefGoogle Scholar
Zhang, L. & Wang, M. 2015 Modeling of electrokinetic reactive transport in micropore using a coupled lattice Boltzmann method. J. Geophys. Res. 120 (5), 2877–2890.Google Scholar
Supplementary material: File

Zhang et al supplementary material

Zhang et al supplementary material 1

Download Zhang et al supplementary material(File)
File 174.8 KB