Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-08T02:00:51.454Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional mode selection of the flow past a rotating and inline oscillating cylinder

Published online by Cambridge University Press:  19 September 2018

David Lo Jacono Open the ORCID record for David Lo Jacono [Opens in a new window] ,
Rémi Bourguet Open the ORCID record for Rémi Bourguet [Opens in a new window] ,
Mark C. Thompson  and
Justin S. Leontini
David Lo Jacono*
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
Rémi Bourguet
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
Justin S. Leontini
Affiliation:
Swinburne University of Technology, Hawthorn, Victoria, 3122, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies the transition to three-dimensional flow in the wake of a cylinder immersed in a free stream, where the cylinder is externally forced to continuously rotate about its axis and to linearly oscillate in the streamwise direction. Floquet stability analysis is used to assess the stability of the nominal two-dimensional flows at a Reynolds number 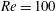$Re=100$ and rotation rate 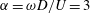$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D714}D/U=3$ to three-dimensional perturbations, as a function of the amplitude and frequency of the linear oscillations. Two modes of instability are found, distinguished by their spatial structure, temporal behaviour and apparent mechanism. The first mode has a shorter wavelength in the spanwise direction and appears to be linked to a centrifugal instability in the layer of fluid near the rotating body. The second mode has a longer wavelength and is linked to an instability of the vortex cores in the wake that is subharmonic, leading to a period doubling. Either mode can be stable while the other is unstable, depending primarily on the frequency of the oscillation of the cylinder. This indicates that either mode can control the transition to a three-dimensional flow. The results are compared to the fully three-dimensional simulation results of a rotating cylinder elastically mounted and free to oscillate in the streamwise direction from Bourguet & Lo Jacono (J. Fluid Mech., vol. 781, 2015, pp. 127–165), and appear to be able to explain the surprising switching of the observed spanwise wavelength in that flow as a change in the dominant mode, and therefore mechanism, of instability.

JFM classification

Instability: Instability Wakes/Jets: Wakes
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , R3
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31 (1), 56–64.Google Scholar
Bourguet, R. & Lo Jacono, D. 2015 In-line flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 781, 127–165.Google Scholar
Gresho, P. M. & Sani, R. L. 1987 On pressure boundary conditions for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 7, 1111–1145.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010 Vortex-induced vibration of a rising and falling cylinder. J. Fluid Mech. 662, 352–383.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2005 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 25–62.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. 2005 Spectral/hp Element Methods for Computation Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2015 Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 763, 302–321.Google Scholar
Parkinson, G. V. & Smith, J. D. 1964 The square prism as an aeroelastic oscillator. Q. J. Mech. Appl. Maths 17 (2), 225–239.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013 Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30 (11), 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for timesteppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems, IMA Volumes in Mathematics and its Applications, vol. 119, pp. 453–466. Springer.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013 Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014 Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar