Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T09:39:46.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory for the rheology of dense non-Brownian suspensions: divergence of viscosities and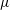$\unicode[STIX]{x1D707}$–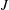$J$ rheology

Published online by Cambridge University Press:  14 February 2019

Koshiro Suzuki Open the ORCID record for Koshiro Suzuki [Opens in a new window]  and
Hisao Hayakawa
Koshiro Suzuki*
Affiliation:
Simulation & Analysis R&D Center, Canon Inc., 30-2 Shimomaruko 3-chome, Ohta-ku, Tokyo 146-8501, Japan
Hisao Hayakawa
Affiliation:
Yukawa Institute for Theoretical Physics, Kyoto University, Kitashirakawaoiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A systematic microscopic theory for the rheology of dense non-Brownian suspensions characterized by the volume fraction 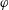$\unicode[STIX]{x1D711}$ is developed. The theory successfully derives the critical behaviour in the vicinity of the jamming point (volume fraction 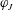$\unicode[STIX]{x1D711}_{J}$), for both the pressure 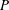$P$ and the shear stress 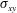$\unicode[STIX]{x1D70E}_{xy}$, i.e. 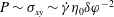$P\sim \unicode[STIX]{x1D70E}_{xy}\sim \dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D702}_{0}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{-2}$, where 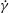$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate, 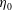$\unicode[STIX]{x1D702}_{0}$ is the shear viscosity of the solvent and 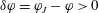$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{J}-\unicode[STIX]{x1D711}>0$ is the distance from the jamming point. It also successfully describes the behaviour of the stress ratio 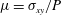$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D70E}_{xy}/P$ with respect to the viscous number 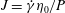$J=\dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D702}_{0}/P$.

JFM classification

Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 1125 - 1176
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alder, B. J. 1964 Triplet correlation in hard spheres. Phys. Rev. Lett. 12, 317–319.Google Scholar
Andreotti, B., Barrat, J.-L. & Heussinger, C. 2012 Shear flow of non-Brownian suspensions close to jamming. Phys. Rev. Lett. 109, 105901.Google Scholar
Bonnoit, C., Darnige, T., Lindner, E. & Clementand, A. 2010 Inclined plane rheometry of a dense granular suspension. J. Rheol. 54, 65–79.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.Google Scholar
Brady, J. F. 1993 The rheological behavior of concentrated colloidal dispersions. J. Chem. Phys. 99, 567–581.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.Google Scholar
Breedveld, V., van den Ende, D., Bosscher, M., Jongschaap, R. J. J. & Mellema, J. 2002 Measurement of the full shear-induced self-diffusion tensor of noncolloidal suspensions. J. Chem. Phys. 116, 10529–10535.Google Scholar
Breedveld, V., van den Ende, D., Tripathi, A. & Acrivos, A. 1998 The measurement of the shear-induced particle and fluid tracer diffusivities in concentrated suspensions by a novel method. J. Fluid Mech. 375, 297–318.Google Scholar
Chamorro, M. G., Reyes, F. V. & Garzó, V. 2015 Non-Newtonian hydrodynamics for a dilute granular suspension under uniform shear flow. Phys. Rev. E 92, 052205.Google Scholar
Chong, J. S., Christiansen, E. B. & Baer, A. D. 1971 Rheology of concentrated suspensions. J. Appl. Polym. Sci. 15, 2007–2021.Google Scholar
Ciamarra, M. P., Coniglio, A. & de Candia, A. 2010 Disordered jammed packings of frictionless spheres. Soft Matt. 6, 2975–2981.Google Scholar
Coulais, C., Seguin, A. & Dauchot, O. 2014 Shear modulus and dilatancy softening in granular packings above jamming. Phys. Rev. Lett. 113, 198001.Google Scholar
Cwalina, C. D. & Wagner, N. J. 2014 Material properties of the shear-thickened state in concentrated near hard-sphere colloidal dispersions. J. Rheol. 58, 949–967.Google Scholar
Dagois-Bohy, S., Hormozi, S., Guazzelli, E. & Pouliquen, O. 2015 Rheology of dense suspensions of non-colloidal spheres in yield-stress fluids. J. Fluid Mech. 776, R2.10.1017/jfm.2015.329Google Scholar
Deboeuf, A., Gauthier, G., Martin, J., Yurkovetsky, Y. & Morris, J. F. 2009 Particle pressure in a sheared suspensions: a bridge from osmosis to granular dilatancy. Phys. Rev. Lett. 102, 108301.Google Scholar
DeGiuli, E., Düring, G., Lerner, E. & Wyart, M. 2015 Unified theory of inertial granular flows and non-Brownian suspensions. Phys. Rev. E 91, 062206.Google Scholar
Donev, A., Torquato, S. & Stillinger, F. H. 2005 Pair correlation function characteristics of nearly jammed disordered and ordered hard-sphere packings. Phys. Rev. E 71, 011105.Google Scholar
Durian, D. J. & Weitz, D. A. 1994 ‘Foams’ in Kirk–Othmer Encyclopedia of Chemical Technology, 4th edn (ed. Kroschwitz, J. I.), p. 783. Wiley.Google Scholar
Einstein, A. 1905 Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen. Ann. Phys. (Berlin) 322, 549–560.Google Scholar
Eisenmann, C., Kim, C., Mattsson, J. & Weitz, D. A. 2010 Shear melting of a colloidal glass. Phys. Rev. Lett. 104, 035502.10.1103/PhysRevLett.104.035502Google Scholar
Foss, D. R. & Brady, J. F. 1999 Self-diffusion in sheared suspensions by dynamic simulation. J. Fluid Mech. 401, 243–274.Google Scholar
Foss, D. R. & Brady, J. F. 2000 Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. J. Fluid Mech. 407, 167–200.Google Scholar
Garzó, V. 2002 Tracer diffusion in granular shear flows. Phys. Rev. E 66, 021308.Google Scholar
Garzó, V. 2013 Grad’s moment method for a granular fluid at moderate densities: Navier–Stokes transport coefficients. Phys. Fluids 25, 043301.Google Scholar
GDR Midi 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.Google Scholar
Glotzer, S. C., Novikov, V. N. & Schröder, T. B. 2000 Time-dependent, four-point density correlation function description of dynamical heterogeneity and decoupling in supercooled liquids. J. Chem. Phys. 112, 509–512.Google Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2, 331–407.Google Scholar
Grouba, V. D., Zorin, A. V. & Sevastianov, L. A. 2004 The superposition approximation: a critical review. Intl J. Mod. Phys. B 18, 1–44.Google Scholar
Hansen, J.-P. & McDonald, I. R. 2006 Theory of Simple Liquids, 3rd edn. Academic Press.Google Scholar
Hayakawa, H. & Takada, S.2016 Kinetic theory of discontinuous shear thickening for a dilute gas–solid suspension. arXiv:1611.07295.Google Scholar
Hayakawa, H. & Takada, S. 2017 Kinetic theory of discontinuous shear thickening. EPJ Web Conf. 140, 09003.Google Scholar
Hayakawa, H., Takada, S. & Garzó, V. 2017 Kinetic theory of shear thickening for a moderately dense gas–solid suspension: from discontinuous thickening to continuous thickening. Phys. Rev. E 96, 042903.Google Scholar
Herdegen, N. & Hess, S. 1982 Nonlinear flow behavior of the Boltzmann gas. Physica A 115, 281–299.Google Scholar
Heussinger, C., Berthier, L. & Barrat, J.-L. 2010 Superdiffusive, heterogeneous, and collective particle motion near the fluid-solid transition in athermal disordered materials. Eur. Phys. Lett. 90, 20005.Google Scholar
Irani, E., Chaudhuri, P. & Heussinger, C. 2014 Impact of attractive interactions on the rheology of dense athermal particles. Phys. Rev. Lett. 112, 188303.Google Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Jenkins, J. T. & McTigue, D. F. 1990 Transport processes in concentrated suspensions: the role of particle fluctuations. In The IMA Volumes in Mathematics and its Applications (ed. Joseph, D. D. & Schaeffer, D. G.). Springer.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985a Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985b Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485–3494.Google Scholar
Kawasaki, T., Coslovich, D., Ikeda, A. & Berthier, L. 2015 Diverging viscosity and soft granular rheology in non-Brownian suspensions. Phys. Rev. E 91, 012203.Google Scholar
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics. Dover.Google Scholar
Kirkwood, J. G. 1935 Statistical mechanics of fluid mixtures. J. Chem. Phys. 3, 300–313.Google Scholar
Kremer, G. M 2010 An Introduction to the Boltzmann Equation and Transport Processes in Gases. Springer.Google Scholar
Krieger, I. M. 1972 Rheology of monodisperse latices. Adv. Colloid Interface Sci. 3, 111–136.Google Scholar
Kuwano, O. & Hatano, T. 2011 Flash weakening is limited by granular dynamics. Geophys. Res. Lett. 38, L17305.Google Scholar
Laun, H. M. 1994 Normal stresses in extremely shear thickening polymer dispersions. J. Non-Newtonian Fluid Mech. 54, 87–108.Google Scholar
Leighton, D. & Acrivos, A. 1987a Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.Google Scholar
Leighton, D. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lootens, D., van Damme, H., Hemar, Y. & Hebraud, P. 2005 Dilatant flow of concentrated suspensions of rough particles. Phys. Rev. Lett. 95, 268302.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. 2014 Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 58, 1693–1724.Google Scholar
Mewis, J. & Wagner, N. J. 2012 Colloidal Suspension Rheology. Cambridge University Press.Google Scholar
Mills, P. & Snabre, P. 2009 Apparent viscosity and particle pressure of a concentrated suspension of non-Brownian hard spheres near the jamming transition. Eur. Phys. J. E 30, 309–316.Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.Google Scholar
O’Hern, C. S., Langer, S. A., Liu, A. J. & Nagel, S. R. 2002 Random packings of frictionless particles. Phys. Rev. Lett. 88, 075507.Google Scholar
O’Hern, C. S., Silbert, L. E., Liu, A. J. & Nagel, S. R. 2003 Jamming at zero temperature and zero applied stress: the epitome of disorder. Phys. Rev. E 68, 011306.Google Scholar
Olsson, P. 2010 Diffusion and velocity autocorrelation at the jamming transition. Phys. Rev. E 81, 040301(R).Google Scholar
Ono, I. K., O’Hern, C. S., Durian, D. J., Langer, S. A., Liu, A. J. & Nagel, S. R. 2002 Effective temperatures of a driven system near jamming. Phys. Rev. Lett. 89, 095703.Google Scholar
Otsuki, M. & Hayakawa, H. 2014 Avalanche contribution to shear modulus of granular materials. Phys. Rev. E 90, 042202.Google Scholar
Parisi, G. 1997 Short-time aging in binary glasses. J. Phys. A 30, L765.Google Scholar
Pusey, P. N. 1991 Liquids, Freezing and Glass Transition, Part II (ed. Hansen, J.-P., Levesque, D. & Zinn-Justin, J.). Elsevier.Google Scholar
Quemada, D. 1977 Rheology of concentrated disperse systems and minimum energy dissipation principle. Rheol. Acta 16, 82–94.Google Scholar
Rotne, J. & Prager, S. 1969 Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 50, 4831–4838.Google Scholar
Saitoh, K. & Hayakawa, H.2019 (in preparation).Google Scholar
Sangani, A. S., Mo, G., Tsao, H.-K. & Koch, D. L. 1996 Simple shear flows of dense gas–solid suspensions at finite Stokes numbers. J. Fluid Mech. 313, 309–341.Google Scholar
Santos, A., Garzó, V. & Dufty, J. W. 2004 Inherent rheology of a granular fluid in uniform shear flow. Phys. Rev. E 69, 061303.Google Scholar
Scala, A., Voigtmann, Th. & Michele, C. D. 2007 Event-driven Brownian dynamics for hard spheres. J. Chem. Phys. 126, 134109.Google Scholar
Seto, R., Mari, R., Morris, J. F. & Denn, M. M. 2013 Phys. Rev. Lett. 111, 218301.Google Scholar
Suzuki, K. & Hayakawa, H. 2015 Divergence of viscosity in jammed granular materials: a theoretical approach. Phys. Rev. Lett. 115, 098001.Google Scholar
Torquato, S. 1995 Nearest-neighbor statistics for packings of hard spheres and disks. Phys. Rev. E 51, 3170–3182.Google Scholar
Tsao, H.-K. & Koch, D. L. 1995 Simple shear flows of dilute gas–solid suspensions. J. Fluid Mech. 296, 211–245.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in newtonian fluids. J. Rheol. 44, 185–220.Google Scholar