Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T08:24:07.248Z Has data issue: false hasContentIssue false
  • English
  • Français

A study of the turbulence within a spiralling vortex filament using proper orthogonal decomposition

Published online by Cambridge University Press:  25 March 2015

Swathi M. Mula  and
Charles E. Tinney
Swathi M. Mula*
Affiliation:
Center for Aeromechanics Research, University of Texas at Austin, Austin, TX 78712, USA
Charles E. Tinney
Affiliation:
Center for Aeromechanics Research, University of Texas at Austin, Austin, TX 78712, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

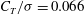The stability and turbulence characteristics of a vortex filament emanating from a single-bladed rotor in hover are investigated using proper orthogonal decomposition (POD). The rotor is operated at a tip chord Reynolds number and tip Mach number of 218 000 and 0.23, respectively, and with a blade loading of $C_{T}/{\it\sigma}=0.066$. In-plane components of the velocity field (normal to the axis of the vortex filament) are captured by way of two-dimensional particle image velocimetry with corrections for vortex wander being performed using the 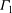${\it\Gamma}_{1}$ method. The first POD mode alone is found to encompass nearly 75 % of the energy for all vortex ages studied and is determined using a grid of sufficient resolution to avoid numerical integration errors in the decomposition. The findings reveal an equal balance between the axisymmetric and helical modes during vortex roll-up, which immediately transitions to helical mode dominance at all other vortex ages. This helical mode is one of the modes of the elliptic instability. The spatial eigenfunctions of the first few Fourier-azimuthal modes associated with the most energetic POD mode is shown to be sensitive to the choice of the wander correction technique used. Higher Fourier-azimuthal modes are observed in the outer portions of the vortex and appeared not to be affected by the choice of the wander correction technique used.

JFM classification

Aerodynamics: Aerodynamics Turbulent Flows: Turbulent Flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 570 - 589
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandyopadhyay, P. R., Stead, D. J. & Robert, L. A. 1991 Organized nature of a turbulent trailing vortex. AIAA J. 29 (10), 1627–1633.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 340, 1–33.Google Scholar
Bhagwat, M. J. & Leishman, J. G. 2000 Stability analysis of helicopter rotor wakes in axial flight. J. Am. Helicopter Soc. 45 (3), 165–178.Google Scholar
Boersma, J. & Wood, D. H. 1999 On the self-induced motion of a helical vortex. J. Fluid Mech. 384, 263–280.Google Scholar
Citriniti, J. H. & George, W. K. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 47 (8), 67–106.Google Scholar
Discetti, S. & Adrian, R. J. 2012 High accuracy measurement of magnification for monocular PIV. Meas. Sci. Technol. 23, 117001.Google Scholar
Fukumoto, Y. & Hattori, Y. 2005 Curvature instability of a vortex ring. J. Fluid Mech. 526, 77–115.Google Scholar
Fukumoto, Y. & Okulov, V. L. 2005 The velocity induced by a helical vortex tube. Phys. Fluids 17 (10), 107101.Google Scholar
Glauser, M. N. & George, W. K. 1987 Orthogonal decomposition of the axisymmetric jet mixing layer including azimuthal dependence. In Advances in Turbulence (ed. Comte-Bellot, G. & Mathieu, J.), pp. 357–366. Springer.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithm for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12, 1422–1429.Google Scholar
Hall, P. 1982 Taylor–Gortler vortices in fully developed boundary layer flows. J. Fluid Mech. 124, 475–494.Google Scholar
Han, Y. O., Leishman, J. G. & Coyne, A. J. 1997 Measurements of the velocity and turbulent structure of a rotor tip vortex. AIAA J. 35 (3), 477–485.Google Scholar
Hattori, Y. & Fukumoto, Y. 2009 Short-wavelength stability analysis of a helical vortex tube. Phys. Fluids 21, 014104.Google Scholar
Hattori, Y. & Fukumoto, Y. 2014 Modal stability analysis of a helical vortex tube with axial flow. J. Fluid Mech. 738, 222–249.Google Scholar
Jung, D., Gamard, S. & George, W. K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 1. The near-field region. J. Fluid Mech. 514, 173–204.Google Scholar
Kerswell, R. R. 2002 Elliptic instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
Kindler, K., Mulleners, K. & Richard, H. 2010 Aperiodicity in the near field of full-scale rotor blade tip vortices. Exp. Fluids 50 (6), 1601–1610.Google Scholar
Lacaze, L., Ryan, K. & Dizes, S. L. 2007 Elliptic instability in a strained Batchelor vortex. J. Fluid Mech. 577, 341–361.Google Scholar
Leishman, J. G. 1996 Seed particle dynamics in tip vortex flows. J. Aircraft 33 (4), 823–825.Google Scholar
Leishman, J. G. 1998 Measurements of the aperiodic wake of a hovering rotor. Exp. Fluids 25, 352–361.Google Scholar
Leishman, J. G., Baker, A. & Coyne, A. 1996 Measurements of rotor tip vortices using three-component laser Doppler velocimetry. J. Am. Helicopter Soc. 41 (4), 342–353.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178. Nauka.Google Scholar
Martin, P. B., Leishman, J. G., Pugliese, G. J. & Anderson, S. L.2000 Stereoscopic PIV measurements in the wake of a hovering helicopter rotor. In Am. Helicopter Soc. Forum 56, May 2–4.Google Scholar
Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425.Google Scholar
Moser, R. D. 1994 Kolmogorov inertial range spectra for inhomogeneous turbulence. Phys. Fluids 6 (2), 794–801.Google Scholar
Mula, S. M., Stephenson, J., Tinney, C. E. & Sirohi, J. 2013 Dynamical characteristics of tip vortex from a four-bladed rotor in hover. Exp. Fluids 54 (10), 1600.Google Scholar
Mula, S. M. & Tinney, C. E.2014 Classical and snapshot forms of the POD technique applied to a helical vortex filament. AIAA Paper 2014-3257.Google Scholar
Nogueira, J., Lecuona, A. & Rodriguez, P. A. 1997 Data validation, false vectors correction and derived magnitudes calculation on PIV data. Meas. Sci. Technol. 18 (12), 1493–1501.Google Scholar
Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2159.Google Scholar
Ragab, S. & Sreedhar, M. 1995 Numerical simulation of vortices with axial velocity deficits. Phys. Fluids 7, 549–558.Google Scholar
Ramasamy, M., Johnson, B., Huismann, T. & Leishman, J. G. 2009a Digital particle image velocimetry measurements of tip vortex characteristics using an improved aperiodicity correction. J. Am. Helicopter Soc. 54, 1–13.Google Scholar
Ramasamy, M., Johnson, B. & Leishman, J. G. 2009b Turbulent tip vortex measurements using dual-plane stereoscopic particle image velocimetry. AIAA J. 47 (8), 1826–1840.Google Scholar
Ramasamy, M. & Leishman, J. G. 2004 Interdependence of diffusion and straining of helicopter blade tip vortices. J. Aircraft 41 (5), 1014–1024.Google Scholar
Ramasamy, M., Timothy, E. L. & Leishman, J. G. 2007 Flowfield of a rotating-wing micro air vehicle. J. Aircraft 44 (4), 1236–1244.Google Scholar
Ricca, R. L. 1994 The effect of torsion on the motion of a helical vortex filament. J. Fluid Mech. 273, 241–259.Google Scholar
Richard, H., Van der Wall, B. G., Raffel, M. & Thimm, M. 2008 Application of PIV techniques for rotor blade tip vortex characterization. In New Results in Numerical and Experimental Fluid Mechanics VI, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 96, pp. 446–453. Springer.Google Scholar
Roy, C., Leweke, T., Thompson, M. C. & Hourigan, K. 2011 Experiments on the elliptic instability in vortex pairs with axial core flow. J. Fluid Mech. 677, 383–416.Google Scholar
Schaeffer, N. & Dizes, S. L. 2010 Non-linear dynamics of the elliptic instability. J. Fluid Mech. 646, 471–480.Google Scholar
Sipp, D. 2000 Weakly nonlinear saturation of short-wave instabilities in a strained Lamb–Oseen vortex. Phys. Fluids 12 (7), 1715–1729.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. J. Appl. Maths 45, 561–590.Google Scholar
Thompson, T. L., Komerath, N. M. & Gray, R. B. 1988 Visualization and measurement of the tip vortex core of a rotor blade in hover. J. Aircraft 25 (12), 1113–1121.Google Scholar
Tinney, C. E., Glauser, M. N. & Ukeiley, L. S. 2008 Low-dimensional characteristics of a transonic jet. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 612, 107–141.Google Scholar
Tsai, C. Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73, 721–733.Google Scholar
Westerweel, J. 1994 Efficient detection of spurious vectors in particle image velocimetry data sets. Exp. Fluids 16, 236–247.Google Scholar
Widnall, S. E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54 (4), 641–663.Google Scholar