Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T14:55:33.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic modelling and diffusion modes for proper orthogonal decomposition models and small-scale flow analysis

Published online by Cambridge University Press:  15 August 2017

Valentin Resseguier Open the ORCID record for Valentin Resseguier [Opens in a new window] ,
Etienne Mémin ,
Dominique Heitz Open the ORCID record for Dominique Heitz [Opens in a new window]  and
Bertrand Chapron
Valentin Resseguier*
Affiliation:
Fluminance, Inria/Irstea/IRMAR, Campus de Beaulieu, 35042 Rennes, France LOPS, Ifremer, Pointe du Diable, 29280 Plouzané, France
Etienne Mémin
Affiliation:
Fluminance, Inria/Irstea/IRMAR, Campus de Beaulieu, 35042 Rennes, France
Dominique Heitz
Affiliation:
Fluminance, Inria/Irstea/IRMAR, Campus de Beaulieu, 35042 Rennes, France Irstea, UR OPAALE, F-35044 Rennes, France
Bertrand Chapron
Affiliation:
LOPS, Ifremer, Pointe du Diable, 29280 Plouzané, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present here a new stochastic modelling approach in the constitution of fluid flow reduced-order models. This framework introduces a spatially inhomogeneous random field to represent the unresolved small-scale velocity component. Such a decomposition of the velocity in terms of a smooth large-scale velocity component and a rough, highly oscillating component gives rise, without any supplementary assumption, to a large-scale flow dynamics that includes a modified advection term together with an inhomogeneous diffusion term. Both of those terms, related respectively to turbophoresis and mixing effects, depend on the variance of the unresolved small-scale velocity component. They bring an explicit subgrid term to the reduced system which enables us to take into account the action of the truncated modes. Besides, a decomposition of the variance tensor in terms of diffusion modes provides a meaningful statistical representation of the stationary or non-stationary structuration of the small-scale velocity and of its action on the resolved modes. This supplies a useful tool for turbulent fluid flow data analysis. We apply this methodology to circular cylinder wake flow at Reynolds numbers 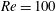$Re=100$ and 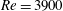$Re=3900$. The finite-dimensional models of the wake flows reveal the energy and the anisotropy distributions of the small-scale diffusion modes. These distributions identify critical regions where corrective advection effects, as well as structured energy dissipation effects, take place. In providing rigorously derived subgrid terms, the proposed approach yields accurate and robust temporal reconstruction of the low-dimensional models.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Turbulent Flows: Turbulence modelling Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 888 - 917
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. & McIntyre, M. 1976 Planetary waves in horizontal and vertical shear: the generalized Eliassen- Palm relation and the zonal mean acceleration. J. Atmos. Sci. 33, 2031–2048.Google Scholar
Artana, G., Cammilleri, A., Carlier, J. & Mémin, E. 2012 Strong and weak constraint variational assimilations for reduced order fluid flow modeling. J. Comput. Phys. 231 (8), 3264–3288.Google Scholar
Aspden, A., Nikiforakis, N., Dalziel, S. & Bell, J. B. 2008 Analysis of implicit LES methods. Appl. Maths Comput. Sci. 3 (1), 103–126.Google Scholar
Aubry, N., Holmes, P., Lumley, J. L. & Stone, E. 1988 The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 192, 115–173.Google Scholar
Bardina, J., Ferziger, J. H. & Reynolds, W. C. 1980 Improved subgrid scale models for large eddy simulation. In 13th Fluid Mechanics & Plasma Dynamics Conference. AIAA.Google Scholar
Boris, J. P., Grinstein, F. F., Oran, E. S. & Kolbe, R. L. 1992 New insights into large-eddy simulation. Fluid Dyn. Res. 10, 199–228.Google Scholar
Boussinesq, J.1877 Essai sur la théorie des eaux courantes. Mémoires présentés par divers savants à l’Académie des Sciences, 23 (1) 1–680.Google Scholar
Brooke, M., Kontomaris, K., Hanratty, T. & McLaughlin., J. 1992 Turbulent deposition and trapping of aerosols at a wall. Phys. Fluids 825–834.Google Scholar
Buffoni, M., Camarri, S., Iollo, A. & Salvetti, M. V. 2006 Low-dimensional modelling of a confined three-dimensional wake flow. J. Fluid Mech. 569, 141–150.Google Scholar
Cammilleri, A., Gueniat, F., Carlier, J., Pastur, L., Mémin, E., Lusseyran, F. & Artana, G. 2013 POD-spectral decomposition for fluid flow analysis and model reduction. Theor. Comput. Fluid Dyn. 27, 787–815.CrossRefGoogle Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in non- isotropic air turbulence. J. Atmos. Sci. 32, 565–568.Google Scholar
Cazemier, W., Verstappen, R. & Veldman, A. 1998 Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 10 (7), 1685–1699.Google Scholar
Chandramouli, P., Heitz, D., Laizet, S. & Mémin, E. 2016 Coarse large-eddy simulations in a transitional wake flow with flow models under location uncertainty. J. Fluid Mech. (submitted).Google Scholar
Cordier, L., Noack, B. R., Tissot, G., Lehnasch, G., Delville, J., Balajewicz, M., Daviller, G. & Niven, R. K. 2013 Identification strategies for model-based control. Exp. Fluids 54 (8), 1–21.Google Scholar
Couplet, M., Basdevant, C. & Sagaut, P. 2005 Calibrated reduced-order POD-Galerkin system for fluid flow modelling. J. Comput. Phys. 207 (1), 192–220.CrossRefGoogle Scholar
D’Adamo, J., Papadakis, N., Mémin, E. & Artana, G. 2007 Variational assimilation of POD low-order dynamical systems. J. Turbul. 8 (9), 1–22.Google Scholar
Deane, A., Kevrekidis, I., Karniadakis, G. & Orszag, S. 1991 Low-dimensional models for complex geometry fows: application to grooved channels and circular cylinders. Phys. Fluids 3 (10), 2337–2354.CrossRefGoogle Scholar
Galetti, B., Botaro, A., Bruneau, C.-H. & Iollo, A. 2007 Accurate model reduction of transient and forced wakes. Eur. J. Mech. (B/Fluids) 26 (3), 354–366.CrossRefGoogle Scholar
Gautier, R., Laizet, S. & Lamballais, E. 2014 A DNS study of jet control with microjets using an immersed boundary method. Intl J. Comput. Fluid Dyn. 28 (6–10), 393–410.Google Scholar
Genon-Catalot, V., Laredo, C. & Picard, D. 1992 Non-parametric estimation of the diffusion coefficient by wavelets methods. Scand. J. Stat. 317–335.Google Scholar
Gent, P., Willebrand, J., Mcdougall, T. & Mcwilliams, J. 1995 Parameterising eddy-induced tracer transports in ocean circulation models. J. Phys. Oceanogr. 25, 463–474.2.0.CO;2>CrossRefGoogle Scholar
Haworth, D. & Pope, S. 1986 A generalized langevin model for turbulent flows. Phys. Fluids 29, 387–405.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherence Structures, Dynamical Systems and Symetry. Cambridge University Press.CrossRefGoogle Scholar
Kalb, V. & Deane, A. 2007 An intrinsic stabilization scheme for proper orthogonal decomposition based low-dimensional models. Phys. Fluids 19 (5), 054106.Google Scholar
Karamanos, G. & Karniadakis, G. 2000 A spectral vanishing viscosity method for large-eddy simulations. J. Comput. Phys. 163 (1), 22–50.Google Scholar
Koopman, B. 1931 Hamiltonian systems and transformations in Hilbert space. Proc. Natl Acad. Sci. USA 17 (5), 315–318.CrossRefGoogle ScholarPubMed
Kraichnan, R. 1987 Eddy viscosity and diffusivity: exact formulas and approximations. Complex Syst. 1 (4–6), 805–820.Google Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with the quasi-spectral accuracy. J. Comput. Phys. 228 (15), 5989–6015.Google Scholar
Lamballais, E., Fortuné, V. & Laizet, S. 2011 Straightforward high-order numerical dissipation via the viscous term for direct and large eddy simulation. J. Comput. Phys. 230, 3270–3275.Google Scholar
Lilly, D. 1992 A proposed modification of the Germano subgrid-scale closure. Phys. Fluids 3, 2746–2757.Google Scholar
Ma, X., Karamanos, G.-S. & Karniadakis, G. E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.Google Scholar
Ma, X., Karniadakis, G. E., Park, H. & Gharib, M. 2002 DPIV-driven simulation: a new computational paradigm. Proc. R. Soc. Lond. A 459, 547–565.Google Scholar
Macinnes, J. & Bracco, F. 1992 Stochastic particles dispersion modelling and the tracer-particle limi. Phys. Fluids 4 (12), 2809–2824.Google Scholar
Mémin, E. 2014 Fluid flow dynamics under location uncertainty. Geophys. Astrophys. Fluid Dyn. 108 (2), 119–146.CrossRefGoogle Scholar
Mezic, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41 (1–3), 309–325.Google Scholar
Noack, B., Morzynski, M. & Tadmor, G. 2010 Reduced-Order Modelling for Flow Control, CISM Courses and Lectures, vol. 528. Springer.Google Scholar
Noack, B., Papas, P. & Monkevitz, P. A. 2005 The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 523, 339–365.Google Scholar
Östh, J., Noack, B., Krajnović, S., Barros, D. & Borée, J. 2014 On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an ahmed body. J. Fluid Mech. 747, 518–544.CrossRefGoogle Scholar
Ouvrard, H., Koobus, B., Dervieux, A. & Salvetti, M. V. 2010 Classical and variational multiscale LES of the flow around a circular cylinder on unstructured grids. Comput. Fluids 39 (7), 1083–1094.CrossRefGoogle Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at reynolds number 3900. Phys. Fluids 20 (8), 085101.Google Scholar
Pasquetti, R. 2006 Spectral vanishing viscosity method for large-eddy simulation of turbulent flows. J. Sci. Comput. 27 (1–3), 365–375.CrossRefGoogle Scholar
Perret, L., Collin, E. & Delville, J. 2006 Polynomial identification of POD based low-order dynamical system. J. Turbul. 7, N17.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid scale backscatter in turbulent and transitional flows. Phys. Fluids 3 (7), 1766–1771.Google Scholar
Pope, S. 1994 Lagrangian pdf methods for turbulent flows. Annu. Rev. Fluid Mech. 26 (1), 23–63.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Protas, B., Noack, B. R & Östh, J. 2015 Optimal nonlinear eddy viscosity in Galerkin models of turbulent flows. J. Fluid Mech. 766, 337–367.CrossRefGoogle Scholar
Reeks, M. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aero. Sci. 14 (6), 729–739.CrossRefGoogle Scholar
Rempfer, D. & Fasel, H. F. 1994 Evolution of three-dimensional coherent structures in a flat-plate boundary layer. J. Fluid Mech. 260, 351–375.Google Scholar
Resseguier, V., Mémin, E. & Chapron, B. 2017a Geophysical flows under location uncertainty, part I: random transport and general models. Geophys. Astrophys. Fluid Dyn. 111 (3), 149–176.Google Scholar
Resseguier, V., Mémin, E. & Chapron, B. 2017b Geophysical flows under location uncertainty, part II: quasi-geostrophic models and efficient ensemble spreading. Geophys. Astrophys. Fluid Dyn. 111 (3), 177–208.Google Scholar
Resseguier, V., Mémin, E. & Chapron, B. 2017c Geophysical flows under location uncertainty, part III. SQG and frontal dynamics under strong turbulence. Geophys. Astrophys. Fluid Dyn. 111 (3), 209–227.CrossRefGoogle Scholar
Rowley, C., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Sawford, B. 1986 Generalized random forcing in random-walk models of turbulent dispersion model. Phys. Fluids 29, 3582–3585.CrossRefGoogle Scholar
Schmid, P. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sehmel, G. 1970 Particle deposition from turbulent air flow. J. Geophys. Res. 75, 1766–1781.Google Scholar
Semaan, R., Kumar, P., Burnazzi, M., Tissot, G., Cordier, L. & Noack, B. R. 2016 Reduced-order modeling of the flow around a high-lift configuration with unsteady coanda blowing. J. Fluid Mech. 800, 72–110.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Q. J. Appl. Maths 45, 561–590.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equation: I. The basic experiment. Mon. Weath. Rev. 91, 99–165.Google Scholar
Tadmor, E. 1989 Convergence of spectral methods for nonlinear conservation laws. SIAM J. Numer. Anal. 26 (1), 30–44.Google Scholar
Takens, F. 1981 Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Lecture Notes in Mathematics, vol. 898, pp. 366–381. Springer.Google Scholar
Yang, Y. & Mémin, E. 2017 High-resolution data assimilation through stochastic subgrid tensor and parameter estimation from 4DEnVar. Tellus A 69 (1), 1308772.Google Scholar