Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-19T14:04:47.741Z Has data issue: false hasContentIssue false
  • English
  • Français

New analytic solutions for wave propagation in flexible, tapered vessels with reference to mammalian arteries

Published online by Cambridge University Press:  17 November 2011

George Papadakis
George Papadakis*
Affiliation:
Department of Aeronautics, Imperial College London, Exhibition Road, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Novel, closed-form, analytic solutions for the pressure and velocity fields are derived for the linear problem of wave propagation inside a tapered flexible vessel of conical shape. It is shown that pressure and velocity can be written in terms of Bessel functions of orders 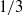and 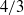respectively. An expression is also derived that quantifies the effect of the cone angle on the wave propagation velocity. The analytic solutions are general and valid for tube variations at any length scale in relation to the wavelength of the wave. In other words, the requirement that the changes in vessel properties with distance should take place over a length scale large compared to the wavelength of the wave, is not employed or needed. This is the basic condition for the application of WKB theory to tapered vessels. However, this condition is not satisfied in pressure pulses propagating in mammalian arteries. The general expressions derived in this paper are directly applicable to the cardiovascular system of mammals. It is further shown that the presented solution naturally tends to the asymptotic WKB solution when the assumptions of the theory are applied to the general expressions. An explicit formula is provided for the time-averaged energy flux of the wave that shows clearly the effect of the continuous reflection of the wave from the vessel wall. Viscous effects are incorporated by coupling the derived analytic solution with the radial velocity profile of Womersley. The results are compared with full nonlinear fluid–structure interaction simulations and very good agreement is found (maximum differences are 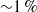and 1.6 % for area-averaged pressure and velocity respectively, and 4–6 % for local velocity values).

JFM classification

Biological Fluid Dynamics: Blood flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 689 , 25 December 2011 , pp. 465 - 488
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alastruey, J., Khir, A. W., Matthys, K. S., Segers, P., Sherwin, S. J., Verdonck, P. R., Parker, K. H. & Peiró, J. 2011 Pulse wave propagation in a model human arterial network: assessment of 1D visco-elastic simulations against in vitro measurements. J. Biomech. 44, 2250–2258.Google Scholar
2. Atabek, H. B. 1968 Wave propagation through a viscous fluid contained in a tethered, initially stressed, orthotropic elastic tube. Biophys. J. 8, 626–649.Google Scholar
3. Atabek, H. B. & Lew, H. S. 1961 Wave propagation through a viscous incompressible fluid contained in an initially stressed elastic tube. Biophys. J. 6, 481–503.Google Scholar
4. Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory. Springer.Google Scholar
5. Bessems, D., Giannopapa, C. G., Rutten, M. C. M. & van de Vosse, F. N. 2008 Experimental validation of a time-domain-based wave propagation model of blood flow in viscoelastic vessels. J. Biomech. 41, 284–291.Google Scholar
6. Bessems, D., Rutten, M. & van de Vosse, F. 2007 A wave propagation model for blood flow in large vessels using an approximate velocity profile function. J. Fluid Mech. 580, 145–168.CrossRefGoogle Scholar
7. Cox, R. H. 1969 Comparison of linearized wave propagation models for arterial blood flow analysis. J. Biomech. 2, 251–265.Google Scholar
8. Einav, S, Aharoni, S. & Manoach, M. 1998 Exponentially tapered transmission line model of the arterial system. IEEE Trans. Biomed. Engng 35 (5), 333–339.Google Scholar
9. Flügge, W. 1960 Stresses in Shells. Springer.Google Scholar
10. Fung, Y. C. 1996 Biomechanics: Circulation, 2nd edn. Springer.Google Scholar
11. Holmes, M. H. 1998 Introduction to Perturbation Methods, Texts in Applied Mathematics , vol. 20. Springer.Google Scholar
12. Hughes, T. J. R & Lubliner, J. 1973 On the one-dimensional theory of blood flow in the large vessels. Math. Biosci. 18, 161–170.CrossRefGoogle Scholar
13. Korteweg, D. J. 1878 Über die Fortpflanzungsgeschwindigkeit des Schalles in elastischen Röhren. Ann. Phys. Chem. (NS) 5, 525–527.Google Scholar
14. LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
15. Lighthill, J. 1975 Pulse propagation theory. In Mathematical Biofluid Dynamics, CBMS-NSF Regional Conference Series in Applied Mathematics , vol. 17. SIAM.CrossRefGoogle Scholar
16. Matthys, K. S., Alastruey, J., Peiro, J., Khir, A. W., Segers, P., Verdonck, P. R., Parker, K. H. & Sherwin, S. J. 2007 Pulse wave propagation in a model human arterial network: assessment of 1D numerical simulations against in vitro measurements. J. Biomech. 40, 3476–3486.Google Scholar
17. Moens, A. I. 1877 Over de Voortplantingssnelheid van den Pols. Van Doesburgh.Google Scholar
18. Myers, L. J. & Capper, W. L. 2004 Exponential taper in arteries: an exact solution of its effect on blood flow velocity waveforms and impedance. Med. Engng Phys. 26, 147–155.Google Scholar
19. Papadakis, G. 2008 A novel pressure–velocity formulation and solution method for fluid–structure-interaction problems. J. Comput. Phys. 227, 3383–3404.CrossRefGoogle Scholar
20. Papadakis, G. 2009 Coupling 3D and 1D fluid–structure-interaction models for wave propagation in flexible vessels using a finite volume pressure-correction scheme. Commun. Numer. Meth. Engng 25, 533–551.CrossRefGoogle Scholar
21. Pedley, T. J. 1980 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.Google Scholar
22. Pedley, T. J. 2000 Blood flow in arteries and veins. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G. ), pp. 105–158. Cambridge University Press.Google Scholar
23. Pedley, T. J. 2003 Mathematical modelling of arterial fluid dynamics. J. Engng Math. 47, 419–444.Google Scholar
24. Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1997 Numerical recipes in Fortran 77. In The Art of Scientific Computing, 2nd edn. Cambridge University Press.Google Scholar
25. Råde, L. & Westergren, B. 1999 Mathematics Handbook for Science and Engineering, 4th edn. Springer.Google Scholar
26. Reymond, P., Merenda, F., Perren, F., Rufenacht, D. & Stergiopoulos, N. 2009 Validation of a one-dimensional model of the systemic arterial tree. Am. J. Physiol. Heart Circ. Physiol. 297, H208–H222.CrossRefGoogle ScholarPubMed
27. Sherwin, S. J., Franke, V., Peiró, J. & Parker, K. 2003 One-dimensional modelling of a vascular network in space–time variables. J. Engng Math. 47, 217–250.CrossRefGoogle Scholar
28. Steele, B. N., Olufsen, M. S. & Taylor, C. A. 2007 Fractal network model for simulating abdominal and lower extremity blood flow during resting and exercise conditions. Comput. Meth. Biomech. Biomed. Engng 10 (1), 39–51.Google Scholar
29. Steele, B. N., Valdez-Jasso, D., Haider, M. A. & Olufsen, M. S. 2011 Predicting arterial flow and pressure dynamics using a 1D fluid dynamics model with a visco-elastic wall. SIAM J. Appl. Math. 71 (4), 1123–1143.Google Scholar
30. Van de Vosse, F. N. & Stergiopoulos, N. 2011 Pulse wave propagation in the arterial tree. Annu. Rev. Fluid Mech. 43, 467–499.Google Scholar
31. Warsi, Z. U. A. 1999 Fluid Dynamics: Theoretical and Computational Approaches, 2nd edn. CRC Press.Google Scholar
32. Witzig, K. 1914 Über erzwungene Wellenbewegungen zäher, inkompressibler Flüssigkeiten in elastischen Röhren. Inaugural Dissertation, University of Bern.Google Scholar
33. Womersley, J. R. 1955 Oscillatory motion of a viscous liquid in a thin-walled elastic tube. Part I. The linear approximation for long waves. Phil. Mag. 46 (7), 199–219.CrossRefGoogle Scholar
34. Womersley, J. R. 1957 Oscillatory flow in arteries: the constrained tube as a model of arterial flow and pulse transmission. Phys. Med. Biol. 2, 178–187.Google Scholar