Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T10:00:26.362Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-field mean flow dynamics of a cylindrical canopy patch suspended in deep water

Published online by Cambridge University Press:  08 November 2018

Jian Zhou  and
Subhas K. Venayagamoorthy Open the ORCID record for Subhas K. Venayagamoorthy [Opens in a new window]
Jian Zhou
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
Subhas K. Venayagamoorthy*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The time-averaged flow dynamics of a suspended cylindrical canopy patch with a bulk diameter of 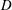$D$ is investigated using large-eddy simulations (LES). The patch consists of 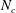$N_{c}$ constituent solid circular cylinders of height 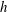$h$ and diameter 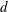$d$, mimicking patchy vegetation suspended in deep water (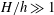$H/h\gg 1$, where 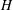$H$ is the total flow depth). After validation against published data, LES of a uniform incident flow impinging on the canopy patch was conducted to study the effects of canopy density (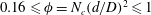$0.16\leqslant \unicode[STIX]{x1D719}=N_{c}(d/D)^{2}\leqslant 1$, by varying 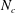$N_{c}$) and bulk aspect ratio (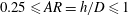$0.25\leqslant AR=h/D\leqslant 1$, by varying 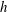$h$) on the near-wake structure and adjustment of flow pathways. The relationships between patch geometry, local flow bleeding (three-dimensional redistribution of flow entering the patch) and global flow diversion (streamwise redistribution of upstream undisturbed flow) are identified. An increase in either 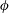$\unicode[STIX]{x1D719}$ or 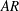$AR$ decreases/increases/increases bleeding velocities through the patch surface area along the streamwise/lateral/vertical directions, respectively. However, a volumetric flux budget shows that a larger 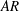$AR$ causes a smaller proportion of the flow rate entering the patch to bleed out vertically. The global flow diversion is found to be determined by both the patch geometrical dimensions and the local bleeding which modifies the sizes of the patch-scale near wake. While loss of flow penetrating the patch increases monotonically with increasing 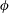$\unicode[STIX]{x1D719}$, its partition into flow diversion around and beneath the patch shows a non-monotonic dependence. The spatial extents of the wake, the flow-diversion dynamics and the bulk drag coefficients of the patch jointly reveal the fundamental differences of flow responses between suspended porous patches and their solid counterparts.

JFM classification

Wakes/Jets: Separated flows Wakes/Jets: Shear layers Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 634 - 655
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adaramola, M. S., Akinlade, O. G., Sumner, D., Bergstrom, D. J. & Schenstead, A. J. 2006 Turbulent wake of a finite circular cylinder of small aspect ratio. J. Fluids Struct. 22, 919–928.Google Scholar
Chang, K. & Constantinescu, G. 2015 Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 776, 161–199.Google Scholar
Chen, Z., Jiang, C. & Nepf, H. 2013 Flow adjustment at the leading edge of a submerged aquatic canopy. Water Resour. Res. 49, 5537–5551.Google Scholar
Chen, Z., Ortiz, A., Zong, L. & Nepf, H. 2012 The wake structure begind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 48, W09517.Google Scholar
Hamed, A. M., Sadowski, M. J., Nepf, H. M. & Chamorro, L. P. 2017 Impact of height heterogeneity on canopy turbulence. J. Fluid Mech. 813, 1176–1196.Google Scholar
Hirt, C. W. 1993 Volume-fraction techniques: power tools for wind engineering. J. Wind Engng Ind. Aerodyn. 46–47, 327–338.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.Google Scholar
Inoue, O. & Sakuragi, A. 2008 Vortex shedding from a circular cylinder of finite length at low Reynolds numbers. Phys. Fluids 20, 033601.Google Scholar
van Leer, B. 1977 Towards the ultimate conservative difference scheme. IV. A new approach to numerical convection. J. Comput. Phys. 23, 276–299.Google Scholar
Leonard, L. A. & Luther, M. E. 1995 Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 40 (8), 1474–1484.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Nepf, H. M. & Vivoni, E. R. 2000 Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 105 (C12), 28547–28557.Google Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.Google Scholar
Plew, D. R. 2011 Depth-averaged coefficient for modeling flow through suspended canopies. J. Hydraul. Engng ASCE 137 (2), 234–247.Google Scholar
Plew, D. R., Spigel, R. H., Stevens, C. L., Nokes, R. I. & Davidson, M. J. 2006 Stratified flow interactions with a suspended canopy. Environ. Fluid Mech. 6, 519–539.Google Scholar
Sakamoto, H. & Arie, M. 1983 Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer. J. Fluid Mech. 126, 147–165.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiments. Mon. Weath. Rev. 91, 99–164.Google Scholar
Sumner, D. 2013 Flow above the free end of a surface-mounted finite-height circular cylinder: A review. J. Fluids Struct. 43, 41–63.Google Scholar
Sumner, D., Heseltine, J. L. & Dansereau, O. J. P. 2004 Wake structure of a finite circular cylinder of small aspect ratio. Exp. Fluids 37 (5), 720–730.Google Scholar
Taddei, S., Manes, C. & Ganapathisubramani, B. 2016 Characterisation of drag and wake properties of canopy patches immersed in turbulent boundary layers. J. Fluid Mech. 798, 27–49.Google Scholar
Tseung, H. L., Kikkert, G. A. & Plew, D. 2016 Hydrodynamics of suspended canopies with limited length and width. Environ. Fluid Mech. 16, 145–166.Google Scholar
Wolverton, B. C. & McDonald, R. C. 1981 Energy from vascular plant wastewater treatment systems. Econ. Bot. 35 (2), 224–232.Google Scholar
Xavier, M. L. M., Janzen, J. G. & Nepf, H. 2018 Numerical modeling study to compare the nutrient removal potential of different floating treatment island configurations in a stormwater pond. Ecol. Engng 111, 78–84.Google Scholar
Yao, G. F.2004 Development of new pressure-velocity solvers in FLOW-3D. Tech. Rep. FSI-04-TN68. Flow Science, Inc.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders, Vol. 1: Fundamentals. Oxford University Press.Google Scholar
Zhou, J., Cenedese, C., Williams, T., Ball, M., Venayagamoorthy, S. K. & Nokes, R. 2017 On the propagation of gravity currents over and through a submerged array of circular cylinders. J. Fluid Mech. 831, 394–417.Google Scholar
Zhou, J. & Venayagamoorthy, S. K. 2017 Numerical simulations of intrusive gravity currents interacting with a bottom-mounted obstacle in a continuously stratified ambient. Environ. Fluid Mech. 17, 191–209.Google Scholar
Zong, L. & Nepf, H. 2012 Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 691, 368–391.Google Scholar