Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T02:45:36.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Mathematical modelling of thermocapillary patterning in thin liquid film: an equilibrium study

Published online by Cambridge University Press:  26 May 2021

Qingzhen Yang Open the ORCID record for Qingzhen Yang [Opens in a new window] ,
Ben Q. Li ,
Xuemeng Lv ,
Fenhong Song ,
Yankui Liu Open the ORCID record for Yankui Liu [Opens in a new window]  and
Feng Xu Open the ORCID record for Feng Xu [Opens in a new window]
Qingzhen Yang
Affiliation:
The Key Laboratory of Biomedical Information Engineering of Ministry of Education, School of Life Science and Technology, Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China Bioinspired Engineering and Biomechanics Center (BEBC), Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China Micro-/Nano-technology Research Center, State Key Laboratory for Manufacturing Systems Engineering, Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China Research Institute of Xi'an Jiaotong University, Hangzhou, Zhejiang311215, PR China
Ben Q. Li
Affiliation:
Department of Mechanical Engineering, University of Michigan-Dearborn, Dearborn, MI48128, USA
Xuemeng Lv
Affiliation:
The Key Laboratory of Biomedical Information Engineering of Ministry of Education, School of Life Science and Technology, Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China Bioinspired Engineering and Biomechanics Center (BEBC), Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China
Fenhong Song
Affiliation:
School of Energy and Power Engineering, Northeast Electric Power University, Jilin, Jilin132012, PR China
Yankui Liu
Affiliation:
School of Energy and Power Engineering, Northeast Electric Power University, Jilin, Jilin132012, PR China
Feng Xu*
Affiliation:
The Key Laboratory of Biomedical Information Engineering of Ministry of Education, School of Life Science and Technology, Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China Bioinspired Engineering and Biomechanics Center (BEBC), Xi'an Jiaotong University, Xi'an, Shaanxi710049, PR China
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

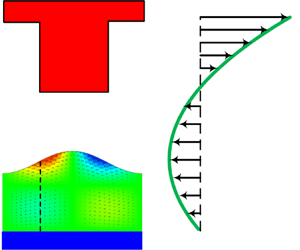
Thermocapillary patterning, namely, the formation of micro/nano patterns in a liquid film by surface deformation induced by an imposed thermal gradient, has enjoyed widespread applications in engineering. In this paper, we present the development of analytical and numerical models and model analyses to predict the equilibrium states of a deformed liquid polymer film under the action of thermocapillary forces. The deformation is found to be dependent on a non-dimensional parameter $\Im \equiv Ma \, Ca$, with Ma denoting the Marangoni number and Ca the capillary number. Model analyses show that a hysteresis phenomenon is associated with the thermocapillary deformation of the film with increasing and then decreasing $\Im$. When $\Im$ is increased above a critical value ${\Im _{c,1}}$, significant deformation occurs in the film until the polymer touches the top solid template. Then, if $\Im$ is allowed to decrease, the polymer film would not detach from the template until $\Im$ is decreased below another critical value ${\Im _{c,2}}$ (usually ${\Im _{c,2}} < {\Im _{c,1}}$). With $\Im \in [{\Im _{c,2}},\;{\Im _{c,1}}]$, there exist multiple (three at the maximum) equilibrium states. The Lyapunov energy analysis of these states reveals that one equilibrium state is stable, another is metastable and the third one is unstable.

JFM classification

Convection: Marangoni convection Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 919 , 25 July 2021 , A29
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arshad, T.A., Kim, C.B., Prisco, N.A., Katzenstein, J.M., Janes, D.W., Bonnecaze, R.T. & Ellison, C.J. 2014 Precision Marangoni-driven patterning. Soft Matt. 10 (40), 8043–8050.CrossRefGoogle ScholarPubMed
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.CrossRefGoogle Scholar
Cengel, Y.A. 2010 Fluid Mechanics. Tata McGraw-Hill Education.Google Scholar
Davis, S.H. 1987 Thermocapillary instabilities. Annu. Rev. Fluid Mech. 19 (1), 403–435.CrossRefGoogle Scholar
Dietzel, M. & Troian, S.M. 2009 Formation of nanopillar arrays in ultrathin viscous films: the critical role of thermocapillary stresses. Phys. Rev. Lett. 103 (7), 074501.CrossRefGoogle ScholarPubMed
Dietzel, M. & Troian, S.M. 2010 Mechanism for spontaneous growth of nanopillar arrays in ultrathin films subject to a thermal gradient. J. Appl. Phys. 108 (7), 074308.CrossRefGoogle Scholar
Fiedler, K.R., McLeod, E. & Troian, S.M. 2019 Differential colorimetry measurements of fluctuation growth in nanofilms exposed to large surface thermal gradients. J. Appl. Phys. 125 (6), 065303.CrossRefGoogle Scholar
Fiedler, K.R. & Troian, S.M. 2016 Early time instability in nanofilms exposed to a large transverse thermal gradient: improved image and thermal analysis. J. Appl. Phys. 120 (20), 205303.CrossRefGoogle Scholar
Li, X., Ding, Y., Shao, J., Tian, H. & Liu, H. 2012 Fabrication of microlens arrays with well-controlled curvature by liquid trapping and electrohydrodynamic deformation in microholes. Adv. Mater. 24 (23), 165–169.CrossRefGoogle ScholarPubMed
Li, X., Tian, H., Shao, J., Ding, Y., Chen, X., Wang, L. & Lu, B. 2016 Decreasing the saturated contact angle in electrowetting-on-dielectrics by controlling the charge trapping at liquid-solid interfaces. Adv. Funct. Mater. 26 (18), 2994–3002.CrossRefGoogle Scholar
Lind, J.U., Busbee, T.A., Valentine, A.D., Pasqualini, F.S., Yuan, H., Yadid, M., Park, S.J., Kotikian, A., Nesmith, A.P. & Campbell, P.H. 2017 Instrumented cardiac microphysiological devices via multimaterial three-dimensional printing. Nat. Mater. 16 (3), 303–308.CrossRefGoogle ScholarPubMed
Liu, Q., Ouchi, T., Jin, L., Hayward, R. & Suo, Z. 2019 Elastocapillary crease. Phys. Rev. Lett. 122 (9), 098003.CrossRefGoogle ScholarPubMed
Mark, J.E. 2009 Polymer Data Handbook. Oxford University Press.Google Scholar
McLeod, E., Liu, Y. & Troian, S.M. 2011 Experimental verification of the formation mechanism for pillar arrays in nanofilms subject to large thermal gradients. Phys. Rev. Lett. 106 (17), 175501.CrossRefGoogle ScholarPubMed
Merkt, D., Pototsky, A., Bestehorn, M. & Thiele, U. 2005 Long-wave theory of bounded two-layer films with a free liquid-liquid interface: short-and long-time evolution. Phys. Fluids 17 (6), 064104.CrossRefGoogle Scholar
Mukherjee, R. & Sharma, A. 2015 Instability, self-organization and pattern formation in thin soft films. Soft Matt. 11 (45), 8717–8740.CrossRefGoogle ScholarPubMed
Nazaripoor, H., Flynn, M.R., Koch, C.R. & Sadrzadeh, M. 2018 Thermally induced interfacial instabilities and pattern formation in confined liquid nanofilms. Phys. Rev. E 98 (4), 043106.CrossRefGoogle Scholar
Nazaripoor, H., Koch, C.R. & Sadrzadeh, M. 2017 Enhanced electrically induced micropatterning of confined thin liquid films: thermocapillary role and its limitations. Ind. Engng Chem. Res. 56 (38), 10678–10688.CrossRefGoogle Scholar
Nazaripoor, H., Koch, C.R., Sadrzadeh, M. & Bhattacharjee, S. 2016 Thermo-electrohydrodyna- mic patterning in nanofilms. Langmuir 32 (23), 5776–5786.CrossRefGoogle Scholar
Rodríguez-Hernández, J. 2015 Wrinkled interfaces: taking advantage of surface instabilities to pattern polymer surfaces. Prog. Polym. Sci. 42, 1–41.CrossRefGoogle Scholar
Ruyer-Quil, C., Scheid, B., Kalliadasis, S., Velarde, M.G. & Zeytounian, R.K. 2005 Thermocapillary long waves in a liquid film flow. Part 1. Low-dimensional formulation. J. Fluid Mech. 538, 199–222.CrossRefGoogle Scholar
Saenz, P.J., Valluri, P., Sefiane, K., Karapetsas, G. & Matar, O. 2013 Linear and nonlinear stability of hydrothermal waves in planar liquid layers driven by thermocapillarity. Phys. Fluids 25 (9), 94101.CrossRefGoogle Scholar
Saprykin, S., Trevelyan, P.M.J., Koopmans, R.J. & Kalliadasis, S. 2007 Free-surface thin-film flows over uniformly heated topography. Phys. Rev. E 75 (2), 026306.CrossRefGoogle ScholarPubMed
Savva, N. & Kalliadasis, S. 2009 Two-dimensional droplet spreading over topographical substrates. Phys. Fluids 21 (9), 092102.CrossRefGoogle Scholar
Savva, N. & Kalliadasis, S. 2011 Dynamics of moving contact lines: a comparison between slip and precursor film models. Europhys. Lett. 94 (6), 64004.CrossRefGoogle Scholar
Schäffer, E., Harkema, S., Roerdink, M., Blossey, R. & Steiner, U. 2003 Thermomechanical lithography: pattern replication using a temperature gradient driven instability. Adv. Mater. 15 (6), 514–517.CrossRefGoogle Scholar
Scheid, B., Ruyer-Quil, C., Kalliadasis, S., Velarde, M.G. & Zeytounian, R.K. 2005 Thermocapillary long waves in a liquid film flow. Part 2. Linear stability and nonlinear waves. J. Fluid Mech. 538, 223–244.CrossRefGoogle Scholar
Sherwood, J.D. 1988 Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 188, 133–146.CrossRefGoogle Scholar
Singer, J.P. 2017 Thermocapillary approaches to the deliberate patterning of polymers. J. Polym. Sci. B: Polym. Phys. 55 (22), 1649–1668.CrossRefGoogle Scholar
Song, F., Ju, D., Fan, J., Chen, Q. & Yang, Q. 2019 Deformation hysteresis of a water nano-droplet in an electric field. Eur. Phys. J. E 42 (9), 120–129.CrossRefGoogle Scholar
Thiele, U., Brusch, L., Bestehorn, M. & Bär, M. 2003 Modelling thin-film dewetting on structured substrates and templates: bifurcation analysis and numerical simulations. Eur. Phys. J. E 11 (3), 255–271.CrossRefGoogle ScholarPubMed
Thiele, U., Neuffer, K., Pomeau, Y. & Velarde, M.G. 2002 On the importance of nucleation solutions for the rupture of thin liquid films. Colloids Surf. A: Physicochem. Engng Aspects 206 (1–3), 135–155.CrossRefGoogle Scholar
Thiele, U., Velarde, M.G., Neuffer, K. & Pomeau, Y. 2001 Film rupture in the diffuse interface model coupled to hydrodynamics. Phys. Rev. E 64 (3), 031602.CrossRefGoogle ScholarPubMed
Trice, J., Favazza, C., Thomas, D., Garcia, H., Kalyanaraman, R. & Sureshkumar, R. 2008 Novel self-organization mechanism in ultrathin liquid films: theory and experiment. Phys. Rev. Lett. 101 (1), 017802.CrossRefGoogle ScholarPubMed
Wu, N., Kavousanakis, M.E. & Russel, W.B. 2010 Coarsening in the electrohydrodynamic patterning of thin polymer films. Phys. Rev. E 81 (2), 026306.CrossRefGoogle ScholarPubMed
Wu, N., Pease, L.F. & Russel, W.B. 2005 Electric-field-induced patterns in thin polymer films: weakly nonlinear and fully nonlinear evolution. Langmuir 21 (26), 12290–12302.CrossRefGoogle ScholarPubMed
Wu, N. & Russel, W.B. 2005 Dynamics of the formation of polymeric microstructures induced by electrohydrodynamic instability. Appl. Phys. Lett. 86 (24), 241912.CrossRefGoogle Scholar
Wu, N. & Russel, W.B. 2006 Electrohydrodynamic instability of dielectric bilayers: kinetics and thermodynamics. Indus. Engng Chem. Res. 45 (16), 5455–5465.CrossRefGoogle Scholar
Yang, Q., Li, B. & Ding, Y. 2013 A numerical study of nanoscale electrohydrodynamic patterning in a liquid film. Soft Matt. 9 (12), 3412–3423.CrossRefGoogle Scholar
Yang, Q., Li, B., Tian, H., Li, X., Shao, J., Chen, X. & Xu, F. 2016 Deformation hysteresis of electrohydrodynamic patterning on a thin polymer film. ACS Appl. Mater. Interfaces 8 (27), 17668–17675.CrossRefGoogle ScholarPubMed