Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T02:27:46.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Intermittency of laminar separation bubble on a sphere during drag crisis

Published online by Cambridge University Press:  05 January 2017

Rahul Deshpande ,
Vivek Kanti ,
Aditya Desai  and
Sanjay Mittal
Rahul Deshpande
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP 208016, India
Vivek Kanti
Affiliation:
National Wind Tunnel Facility, Indian Institute of Technology Kanpur, UP 208016, India
Aditya Desai
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP 208016, India
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP 208016, India National Wind Tunnel Facility, Indian Institute of Technology Kanpur, UP 208016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The phenomenon of drag crisis for uniform flow past a smooth sphere is investigated via experiments in a low-turbulence wind tunnel for 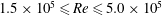$1.5\times 10^{5}\leqslant Re\leqslant 5.0\times 10^{5}$. The Reynolds number, 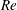$Re$, is based on the free-stream speed and the diameter of the sphere. Based on the activity related to the laminar separation bubble (LSB), the critical regime for the occurrence of drag crisis (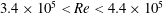$3.4\times 10^{5}<Re<4.4\times 10^{5}$) is further divided into three subregimes. The gradual decrease of mean drag coefficient (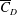$\overline{C}_{D}$) with 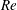$Re$, in subregime I, is due to the increase of base pressure and suction near the shoulder of the sphere. The flow is devoid of an LSB in this regime. The coefficient 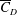$\overline{C}_{D}$ decreases very rapidly with increase in $Re$ in subregime II primarily due to the increase in mean base pressure (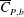$\overline{C}_{P,b}$). This subregime is characterized by intermittent switching of 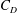$C_{D}$ and 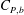$C_{P,b}$ between bistable states. Statistical analysis of the surface-pressure and force coefficients relates this behaviour to the intermittent appearance/disappearance of the LSB. The two states of the flow are referred to as the LSB and non-LSB states. The frequency of appearance of the LSB and the duration of its stay increase with increase in 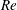$Re$. An intermittency factor 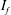$I_{f}$, defined as the fraction of time during which the LSB exists in the flow, is estimated at each 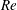$Re$. The value of 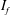$I_{f}$ is zero in subregime I and increases from zero to one, with increase in 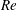$Re$, in subregime II. The variation of 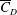$\overline{C}_{D}$ with 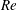$Re$ is found to follow the variation of (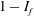$1-I_{f}$) with 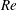$Re$. This shows that the decrease of $\overline{C}_{D}$ with increase in $Re$, during drag crisis, is primarily due to the increased probability of the LSB state as opposed to the non-LSB state. A spatio-temporal analysis of the surface pressure measured at various polar locations on the surface of the sphere confirms the axisymmetric nature of the intermittent LSB. In subregime III of the critical regime, the LSB exists at all time instants (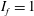$I_{f}=1$). The 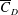$\overline{C}_{D}$ value continues to decrease with 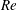$Re$ in this subregime due to increase in 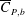$\overline{C}_{P,b}$. Unlike the general belief that the decrease in 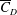$\overline{C}_{D}$ with increase in 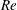$Re$ is due only to the increase in 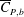$\overline{C}_{P,b}$, it is found that the increase in suction upstream of the shoulder of the sphere, with increase in 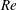$Re$, also plays an important role. In particular, in the high subcritical regime (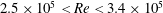$2.5\times 10^{5}<Re<3.4\times 10^{5}$), the gradual decrease in 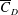$\overline{C}_{D}$ with increase in 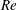$Re$ is due solely to the increase in suction in a region upstream of the shoulder of the sphere.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer separation Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 815 - 840
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1971 Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 46 (02), 321–335.CrossRefGoogle Scholar
Achenbach, E. 1972 Experiments on the flow past spheres at very high Reynolds numbers. J. Fluid Mech. 54 (03), 565–575.CrossRefGoogle Scholar
Achenbach, E. 1974 The effects of surface roughness and tunnel blockage on the flow past spheres. J. Fluid Mech. 65 (01), 113–125.CrossRefGoogle Scholar
Cadot, O., Desai, A., Mittal, S., Saxena, S. & Chandra, B. 2015 Statistics and dynamics of the boundary layer reattachments during the drag crisis transitions of a circular cylinder. Phys. Fluids 27 (1), 014101.Google Scholar
Chopra, G. & Mittal, S. 2017 The intermittent nature of the laminar separation bubble on a cylinder in uniform flow. Comput. Fluids 142, 118–127.CrossRefGoogle Scholar
Fage, A.1937 Experiments on a sphere at critical Reynolds numbers. Aeronautical Research Council Reports and Memoranda No. 1776.Google Scholar
Hoerner, S.1935 Tests of spheres with reference to Reynolds number, turbulence, and surface roughness. Technical Memorandum No. 777, National Advisory Committee for Aeronautics.Google Scholar
Jeon, S., Choi, J., Jeon, W.-P., Choi, H. & Park 2004 Active control of flow over a sphere for drag reduction at a subcritical Reynolds number. J. Fluid Mech. 517, 113–129.CrossRefGoogle Scholar
Kim, H. J. & Durbin, P. A. 1988 Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 31 (11), 3260–3265.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics, 1959. Pergamon.Google Scholar
Miau, J. J., Tsai, H. W., Lin, Y. J., Tu, J. K., Fang, C. H. & Chen, M. C. 2011 Experiment on smooth, circular cylinders in cross-flow in the critical Reynolds number regime. Exp. Fluids 51 (4), 949–967.CrossRefGoogle Scholar
Norman, A. K., Kerrigan, E. C. & McKeon, B. J. 2011 The effect of small-amplitude time-dependent changes to the surface morphology of a sphere. J. Fluid Mech. 675, 268–296.CrossRefGoogle Scholar
Norman, A. K. & McKeon, B. J. 2008 Effect of sting size on the wake of a sphere at subcritical Reynolds numbers. In AIAA 8th Fluid Dyn. Conf. and Exhibit.Google Scholar
Norman, A. K. & McKeon, B. J. 2011 Unsteady force measurements in sphere flow from subcritical to supercritical Reynolds numbers. Exp. Fluids 51 (5), 1439–1453.CrossRefGoogle Scholar
Schewe, G. 1983 On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 133, 265–285.CrossRefGoogle Scholar
Singh, S. P. & Mittal, S. 2005 Flow past a cylinder: shear layer instability and drag crisis. Intl J. Numer. Meth. Fluids 47 (1), 75–98.CrossRefGoogle Scholar
Solliec, C. & Mary, J. 1995 Simultaneous measurements of fluctuating pressures using piezoresistive multichannel transducers as applied to atmospheric wind tunnel tests. J. Wind Engng Ind. Aerodyn. 56 (1), 71–86.CrossRefGoogle Scholar
Suryanarayana, G. K. & Meier, G. E. A. 1995 Effect of ventilation on the flowfield around a sphere. Exp. Fluids 19 (2), 78–88.CrossRefGoogle Scholar
Suryanarayana, G. K., Pauer, H. & Meier, G. E. A. 1993 Bluff-body drag reduction by passive ventilation. Exp. Fluids 16 (2), 73–81.CrossRefGoogle Scholar
Suryanarayana, G. K. & Prabhu, A. 2000 Effect of natural ventilation on the boundary layer separation and near-wake vortex shedding characteristics of a sphere. Exp. Fluids 29 (6), 582–591.CrossRefGoogle Scholar
Taneda, S. 1978 Visual observations of the flow past a sphere at Reynolds numbers between 104 and 106 . J. Fluid Mech. 85 (01), 187–192.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Wieselsberger, C. 1922 Neuere feststellungen über die gesetze des flüssigkeits- und luftwiderstandes. Phys. Z. 22 (11), 321–328.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar