Published online by Cambridge University Press: 27 October 2021
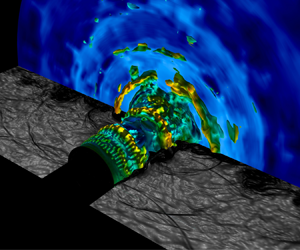
In this study, large-eddy simulations are utilised to unravel the influence of the nozzle's external geometry on upstream-travelling waves in under-expanded supersonic impinging jets. Three configurations, a thin-lipped, a thin-lipped with a sponge and an infinite-lipped nozzle are considered with the other non-dimensionalised geometrical and flow variables identical for the three cases. Spectral proper orthogonal decomposition is applied to the Mack norm, i.e. the energy norm based on the stagnation energy, to obtain the spatial modes at their corresponding frequency. The spectral decomposition of the spatial modes at optimal and suboptimal frequencies is used to isolate the wavepackets into upstream- and downstream-propagating waves based on their phase velocity. It is found that the external geometry of the nozzle has a significant influence on the first-order statistics even though the governing non-dimensional parameters are the same for all three cases. Multiple peaks emerge in the energy spectra at distinct frequencies corresponding to axisymmetric azimuthal modes for each case. The downstream-propagating wavepackets have a high amplitude at the shear layer of the three jets with the mode shapes resembling Kelvin–Helmholtz instability waves, while the upstream-travelling wavepackets exist in the three regions of the near field, shear layer and inside of the jet. The barrel shock at the nozzle exit appears as a flexible shield, which prevents upstream-travelling waves from reaching the internal region of the nozzle, where the upstream-travelling waves travel obliquely with one side of the wavefront is crawling on the reflected shock while the other side is guided by the shear layer. These latter waves can reach the nozzle lip via inside of the jet. The spectral decomposition of the spatial modes at optimal and suboptimal frequencies show that all three forms of the near field, shear layer and inside jet upstream-travelling wavepackets contribute to the receptivity process while their contributions and strength are altered by the change of the external geometry of the nozzle.