Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-19T06:02:30.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Frontal waves in a strait

Published online by Cambridge University Press:  25 February 2008

MELVIN E. STERN  and
JULIAN A. SIMEONOV
MELVIN E. STERN
Affiliation:
Department of Oceanography, Florida State University, Tallahassee, FL 32306-4320, [email protected]; [email protected]
JULIAN A. SIMEONOV
Affiliation:
Department of Oceanography, Florida State University, Tallahassee, FL 32306-4320, [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The slow downstream (x) variation of a dense and inviscid bottom current (u) in a parabolic strait with a sill at y = 0 is investigated. Vanishing potential vorticity is assumed and the density interface in the 1 1/2-layer model intersects the bottom at y = y1 and y = y2 < y1, where the vanishing layer thickness (h) provides the free dynamical boundary condition. For time-dependent finite-amplitude waves, the nonlinear hyperbolic equations obtained here give the wave velocity and indicate the sense in which lateral wave steepening occurs. The long-wave perturbations of y1(x,t), y2(x,t) are stationary if 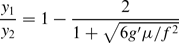where g′ is the reduced gravity, μ = ∂2M/∂y2 is the parabolic curvature of the bottom elevation (M), and f is the Coriolis parameter. This controls the upstream–downstream flow, and the downstream nonlinearity generates ‘short’ waves which may initiate lateral mixing with the adjacent (less dense) water mass.

It is also shown that short waves are exponentially amplified with a maximum growth rate (about 1/day) depending only on g′μ/f2. When g′μ/f2 = 1 (a narrow strait) the instability is suppressed, but for small g′μ/f2≪1 the growth rate is comparable to the flat bottom case μ = 0, studied by Griffiths, Killworth & Stern (J. Fluid Mech. Vol. 117, 1982, p. 343.).

Type
Papers
Information
Journal of Fluid Mechanics , Volume 598 , 10 March 2008 , pp. 321 - 334
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Borenäs, K. & Lundberg, P. 1986 Rotating hydraulics of flow in a parabolic channel. J. Fluid Mech. 167, 309–326.CrossRefGoogle Scholar
Borenäs, K. M. & Lundberg, P. 1988 On the deep-water flow through the Faroe Bank Channel. J. Geophys. Res. 93 (C2), 1281–1292.CrossRefGoogle Scholar
Cenedese, C., Whitehead, J. A., Ascarelli, T. A. & Ohiwa, M. 2004 A dense current flowing down a sloping bottom in a rotating fluid. J. Phys. Oceanogr. 31, 1904–1914.Google Scholar
Ezer, T. 2006 Topographic influence on overflow dynamics: Idealized numerical simulations and the Faroe Bank Channel overflow. J. Geophys. Res. 111, C02002, doi:10.1029/2005JC003195.CrossRefGoogle Scholar
Geyer, F., Osterhus, S., Hansen, B. & Quadfasel, D. 2006 Observations of highly regular oscillations in the overflow plume downstream of the Faroe Bank Channel. J. Geophys. Res. 111, C12020, doi:10.1029/2006JC003693.CrossRefGoogle Scholar
Gill, A. E. 1977 The hydraulics of rotating-channel flow. J. Fluid Mech. 80, 641–671.CrossRefGoogle Scholar
Girton, J. B. & Sanford, T. B. 2002 A process study of the Denmark Strait Overflow. The 2nd Meeting on the Physical Oceanography of Sea Straits, Villefranche, 15–19 April 2002, pp. 107–111.Google Scholar
Girton, J. B., Sanford, T. B. & Käse, R. H. 2001 Synoptic sections of the Denmark Strait overflow. Geophys. Res. Lett. 28 (eq9), 1619–1622.CrossRefGoogle Scholar
Griffiths, R. W., Killworth, P. D. & Stern, M. E. 1982 Ageostrophic instability of ocean currents. J. Fluid Mech. 117, 343–377.CrossRefGoogle Scholar
Karsten, R. H., Swaters, G. E. & Thomson, R. E. 1995 Stability characteristics of deep-water replacement in the Strait of Georgia. J. Phys. Oceanogr. 25, 2391–2403.2.0.CO;2>CrossRefGoogle Scholar
Käse, R. H., Girton, J. B. & Sanford, T. B. 2003 Structure and variability of the Denmark Strait overflow: Model and observations. J. Geophys. Res. 108 (C6), 3181.CrossRefGoogle Scholar
Käse, R. H. & Oschlies, A. 2000 Flow through Denmark Strait. J. Geophys. Res. 105, 28527–28546.CrossRefGoogle Scholar
Paldor, N. 1983 Stability and stable modes of coastal fronts. Geophys. Astrophys. Fluid Dyn. 27, 217–228.CrossRefGoogle Scholar
Pratt, L. & Helfrich, K. 2007 On the stability of ocean overflows. J. Fluid Mech. submitted.CrossRefGoogle Scholar
Pratt, L. J., Helfrich, K. R. & Chassignet, E. P. 2000 Hydraulic adjustment to an obstacle in a rotating channel. J. Fluid Mech. 404, 117–149.CrossRefGoogle Scholar
Stern, M. E. 1980 Geostrophic fronts, bores, breaking and block waves. J. Fluid Mech. 99 (4), 687–703.CrossRefGoogle Scholar
Stern, M. E. & Chassignet, E. P. 2000 Mechanism of eddy separation from coastal currents. J. Mar. Res. 58, 269–295.CrossRefGoogle Scholar
Stern, M. E. & Helfrich, K. 2002 Propagation of a finite-amplitude potential vorticity front along the wall of a stratified fluid. J. Fluid Mech. 468, 179–204.CrossRefGoogle Scholar
Whitehead, J. A. 1998 Topographic control of oceanic flow in deep passages and straits. Rev. Geophys. 36 (3), 423–440.CrossRefGoogle Scholar
Whitehead, J. A., Leetmaa, A. & Knox, R. A. 1974 Rotating hydraulics of strait and sill flows. Geophys. Fluid Dyn. 6, 101–125.CrossRefGoogle Scholar