Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-03T09:03:01.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental survey of linear and nonlinear inertial waves and wave instabilities in a spherical shell

Published online by Cambridge University Press:  25 January 2016

Michael Hoff ,
U. Harlander  and
C. Egbers
Michael Hoff*
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology (BTU) Cottbus – Senftenberg, 03046 Cottbus, Germany
U. Harlander
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology (BTU) Cottbus – Senftenberg, 03046 Cottbus, Germany
C. Egbers
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology (BTU) Cottbus – Senftenberg, 03046 Cottbus, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally study linear and nonlinear inertial waves in a spherical shell with a radius ratio of 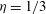${\it\eta}=1/3$. The shell rotates with a mean angular velocity 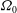${\it\Omega}_{0}$ around its vertical axis. This rotation is overlaid by a time-periodic libration of the inner sphere in the range 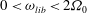$0<{\it\omega}_{lib}<2{\it\Omega}_{0}$ to excite inertial waves with a defined frequency. In the first part, we investigate linear inertial waves. The influence of the libration amplitude and the libration frequency on the waves and further the efficiency of the forcing to excite linear inertial waves will be discussed. For this, qualitative data from Kalliroscope visualisation in a meridional laser plane, as well as quantitative particle image velocimetry (PIV) data in a horizontal plane, have been analysed. A simple two-dimensional ray-tracing model is applied for the meridional plane to interpret the visualisations with respect to energy focusing and wave attractors. For sufficiently high/low libration amplitudes/frequencies, the Stewartson layer, a vertical shear layer tangential to the inner sphere’s equator, becomes unstable. This so-called ‘supercritical’ regime, where centrifugal and shear instabilities occur, allows for nonlinear wave coupling. PIV analyses in the horizontal laser plane in the corotating frame show low-frequency structures that correspond to Rossby-wave instabilities of the Stewartson layer. Some of these are travelling retrograde and are trapped near the Stewartson layer, others are travelling prograde filling the whole gap outside the Stewartson layer. Since libration can be viewed as a time-periodic variation of differential rotation, we assume that these two different structures are related to either the retrograde 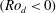$(Ro_{d}<0)$ or the prograde 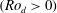$(Ro_{d}>0)$ phase of the libration cycle. The experimental results confirm theoretical, numerical as well as other experimental studies on Stewartson-layer instabilities.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 789 , 25 February 2016 , pp. 589 - 616
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguiar, A. & Read, P. 2006 Instabilities of a barotropic shear layer in a rotating fluid: asymmetries with respect to $\text{sgn}(Ro)$ . Meteorol. Z. 15 (4), 417–422.Google Scholar
Aldridge, K. D. 1972 Axisymmetric inertial oscillations of a fluid in a rotating spherical shell. Mathematika 19 (02), 163–168.Google Scholar
Aldridge, K. D. & Lumb, L. I. 1987 Inertial waves identified in the Earth’s fluid outer core. Nature 325 (6103), 421–423.Google Scholar
Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37 (02), 307–323.Google Scholar
Borcia, I. D., Ghasemi, A. V. & Harlander, U. 2014 Inertial wave mode excitation in a rotating annulus with partially librating boundaries. Fluid Dyn. Res. 46 (4), 041423.Google Scholar
Borcia, I. D. & Harlander, U. 2013 Inertial waves in a rotating annulus with inclined inner cylinder: comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor. Comput. Fluid Dyn. 27 (3–4), 397–413.CrossRefGoogle Scholar
Bordes, G., Moisy, F., Dauxois, T. & Cortet, P.-P. 2012 Experimental evidence of a triadic resonance of plane inertial waves in a rotating fluid. Phys. Fluids 24 (1), 014105.Google Scholar
Bourget, B., Dauxois, T., Joubaud, S. & Odier, P. 2013 Experimental study of parametric subharmonic instability for internal plane waves. J. Fluid Mech. 723, 1–20.Google Scholar
Busse, F. H. 1968 Shear flow instabilities in rotating systems. J. Fluid Mech. 33 (03), 577–589.Google Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22 (8), 086602.Google Scholar
Comstock, R. L. & Bills, B. G. 2003 A solar system survey of forced librations in longitude. J. Geophys. Res. 108, E9.Google Scholar
Egbers, C. & Rath, H. J. 1995 The existence of Taylor vortices and wide-gap instabilities in spherical Couette flow. Acta Mech. 111 (3–4), 125–140.Google Scholar
Emery, W. J. & Thomson, R. E. 2001 Data Analysis Methods in Physical Oceanography, 2nd edn. Elsevier.Google Scholar
Früh, W.-G. & Read, P. L. 1999 Experiments on a barotropic rotating shear layer. Part 1. Instability and steady vortices. J. Fluid Mech. 383, 143–173.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Harlander, U., Larcher, T., Wright, G. B., Hoff, M., Alexandrov, K. & Egbers, C. 2014 Orthogonal decomposition methods to analyze PIV, LDV, and thermography data of thermally driven rotating annulus laboratory experiments. In Modeling Atmospheric and Oceanic Flows (ed. Larcher, T. & Williams, P. D.), pp. 315–336. John Wiley.Google Scholar
Harlander, U. & Maas, L. R. M. 2006 Characteristics and energy rays of equatorially trapped, zonally symmetric internal waves. Meteorol. Z. 15 (4), 439–450.Google Scholar
Harlander, U. & Maas, L. R. M. 2007a Internal boundary layers in a well-mixed equatorial atmosphere/ocean. Dyn. Atmos. Oceans 44 (1), 1–28.Google Scholar
Harlander, U. & Maas, L. R. M. 2007b Two alternatives for solving hyperbolic boundary value problems of geophysical fluid dynamics. J. Fluid Mech. 588, 331–351.Google Scholar
Hide, R. & Titman, C. W. 1967 Detached shear layers in a rotating fluid. J. Fluid Mech. 29 (01), 39.Google Scholar
Hollerbach, R. 2003 Instabilities of the Stewartson layer. Part 1. The dependence on the sign of Ro . J. Fluid Mech. 492, 289–302.Google Scholar
Hollerbach, R., Futterer, B., More, T. & Egbers, C. 2004 Instabilities of the Stewartson layer. Part 2. Supercritical mode transitions. Theor. Comput. Fluid Dyn. 18 (2–4), 197–204.Google Scholar
Hollerbach, R., Junk, M. & Egbers, C. 2006 Non-axisymmetric instabilities in basic state spherical Couette flow. Fluid Dyn. Res. 38 (4), 257–273.Google Scholar
Kerswell, R. R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.Google Scholar
Kida, S. 2011 Steady flow in a rapidly rotating sphere with weak precession. J. Fluid Mech. 680, 150–193.Google Scholar
Klein, M., Seelig, T., Kurgansky, M. V., Ghasemi V., A. V., Borcia, I. D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder. J. Fluid Mech. 751, 255–297.Google Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 035504.Google Scholar
Li, H., Colgate, S. A., Wendroff, B. & Liska, R. 2001 Rossby wave instability of thin accretion disks. III. Nonlinear simulations. Astrophys. J. 551 (2), 874.Google Scholar
Li, H., Finn, J. M., Lovelace, R. V. E. & Colgate, S. A. 2000 Rossby wave instability of thin accretion disks. II. Detailed linear theory. Astrophys. J. 533 (2), 1023.Google Scholar
Maas, L. R. M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.Google Scholar
Manders, A. M. M. & Maas, L. R. M. 2003 Observations of inertial waves in a rectangular basin with one sloping boundary. J. Fluid Mech. 493, 59–88.Google Scholar
Messio, L., Morize, C., Rabaud, M. & Moisy, F. 2008 Experimental observation using particle image velocimetry of inertial waves in a rotating fluid. Exp. Fluids 44 (4), 519–528.Google Scholar
Morize, C., Le Bars, M., Le Gal, P. & Tilgner, A. 2010 Experimental determination of zonal winds driven by tides. Phys. Rev. Lett. 104 (21), 214501.Google Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173 (1–2), 141–152.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Rabitti, A. & Maas, L. R. M. 2013 Meridional trapping and zonal propagation of inertial waves in a rotating fluid shell. J. Fluid Mech. 729, 445–470.Google Scholar
Rabitti, A. & Maas, L. R. M. 2014 Inertial wave rays in rotating spherical fluid domains. J. Fluid Mech. 758, 621–654.Google Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics. Part II. Time-periodic flows. Geophys. Astrophys. Fluid Dyn. 59 (1–4), 185–208.Google Scholar
Rieutord, M. 1995 Inertial modes in the liquid core of the Earth. Phys. Earth Planet. Inter. 91 (1–3), 41–46.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.Google Scholar
Rieutord, M., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2012 Excitation of inertial modes in an experimental spherical Couette flow. Phys. Rev. E 86 (2), 026304.Google Scholar
Sauret, A., Cébron, D. & Le Bars, M. 2013 Spontaneous generation of inertial waves from boundary turbulence in a librating sphere. J. Fluid Mech. 728, R5.CrossRefGoogle Scholar
Sauret, A., Cébron, D., Le Bars, M. & Le Dizès, S. 2012 Fluid flows in a librating cylinder. Phys. Fluids 24 (2), 026603.Google Scholar
Sauret, A., Cébron, D., Morize, C. & Le Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268.Google Scholar
Sauret, A., Le Bars, M. & Le Gal, P. 2014 Tide-driven shear instability in planetary liquid cores. Geophys. Res. Lett. 41 (17), 6078–6083.Google Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.Google Scholar
Schaeffer, N. & Cardin, P. 2005a Quasigeostrophic model of the instabilities of the Stewartson layer in flat and depth-varying containers. Phys. Fluids 17 (10), 104111.Google Scholar
Schaeffer, N. & Cardin, P. 2005b Rossby-wave turbulence in a rapidly rotating sphere. Nonlinear Process. Geophys. 12 (6), 947–953.Google Scholar
Schwierz, C., Dirren, S. & Davies, H. C. 2004 Forced waves on a zonally aligned jet stream. J. Atmos. Sci. 61 (1), 73–87.Google Scholar
Seelig, T. 2014 Inertial Wave Propagation, Focusing and Mean Flow Excitation: Theory and Experiments, 1st edn. Cuvillier.Google Scholar
Spohn, T. 2007 Planets and moons. In Treatise on Geophysics, 1st edn. (ed. Schubert, G.), vol. 10. Elsevier.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3 (01), 17.Google Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26 (01), 131–144.Google Scholar
Sveen, J. K.2004 An introduction to MatPIV v. 1.6.1.Google Scholar
Tilgner, A. 1999 Driven inertial oscillations in spherical shells. Phys. Rev. E 59 (2), 1789–1794.Google Scholar
Triana, S. A.2011 Inertial waves in a laboratory model of the Earth’s core. PhD thesis, University of Maryland.Google Scholar
Wicht, J. 2014 Flow instabilities in the wide-gap spherical Couette system. J. Fluid Mech. 738, 184–221.Google Scholar
Zhang, K., Chan, K. H., Liao, X. & Aurnou, J. M. 2013 The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration. J. Fluid Mech. 720, 212–235.Google Scholar
Zimmerman, D. S., Triana, S. A. & Lathrop, D. P. 2011 Bi-stability in turbulent, rotating spherical Couette flow. Phys. Fluids 23 (6), 065104.Google Scholar
Supplementary material: File

Hoff supplementary material

Hoff supplementary material 1

Download Hoff supplementary material(File)
File 15.1 MB