Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T09:08:17.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental reconstruction of extreme sea waves by time reversal principle

Published online by Cambridge University Press:  09 December 2019

Guillaume Ducrozet Open the ORCID record for Guillaume Ducrozet [Opens in a new window] ,
Félicien Bonnefoy ,
Nobuhito Mori ,
Mathias Fink  and
Amin Chabchoub
Guillaume Ducrozet*
Affiliation:
École Centrale de Nantes, LHEEA Res. Dept. (ECN and CNRS), 44321Nantes, France
Félicien Bonnefoy
Affiliation:
École Centrale de Nantes, LHEEA Res. Dept. (ECN and CNRS), 44321Nantes, France
Nobuhito Mori
Affiliation:
Disaster Prevention Research Institute, Kyoto University, Kyoto611-0011, Japan
Mathias Fink
Affiliation:
Institut Langevin, ESPCI Paris, PSL University, CNRS, UMR CNRS No. 7587, 75005Paris, France
Amin Chabchoub
Affiliation:
Centre for Wind, Waves and Water, School of Civil Engineering, The University of Sydney, Sydney, NSW2006, Australia Marine Studies Institute, The University of Sydney, Sydney, NSW2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

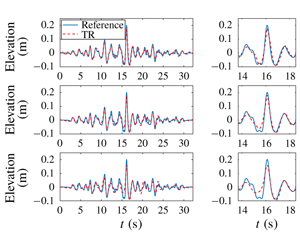
We report an experimental study of the reconstruction of real-ocean rogue waves in a laboratory environment using the time reversal (TR) methodology (Chabchoub & Fink, Phys. Rev. Lett., vol. 112, 2014, 124101). Three different rogue wave measurements are used to validate the TR approach. The generation and accurate control of target free-surface profiles in a unidirectional wave flume using standard techniques, such as the New Wave theory (Tromans, Anaturk & Hagemeier, Proceedings of the First International Offshore and Polar Engineering Conference, 1991, pp. 64–71), are fairly challenging, especially for very steep and, thus, highly nonlinear extreme waves. The TR method, making use of the time reversibility of wave propagation and symmetry of the governing hydrodynamic equations of motion, leads to a simple two-step experimental procedure, the accuracy of which is investigated in this paper. The use of the TR procedure requires the appropriate Froude scaling in designing the model-scale experiments. The present study represents the first validation of the TR method to realistic irregular seas containing rogue waves. Three extreme wave profiles are tested to assess the applicability of the TR scheme to different wave configurations taking into account variable characteristics. This includes the famed New Year wave. The accuracy of the TR method is demonstrated with varying wave steepness values and propagation distances of the reverse reconstruction. It is demonstrated that the unidirectional TR reconstruction is robust, even in the presence of unavoidable wave breaking, known to be an irreversible process within the framework of any wave hydrodynamic evolution equation, and independently of complex environmental conditions or focusing mechanism at play in the sea.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Geophysical and Geological Flows: Ocean processes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A20
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhmediev, N., Ankiewicz, A. & Taki, M. 2009 Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373 (6), 675–678.CrossRefGoogle Scholar
Akhmediev, N., Eleonskii, V. M. & Kulagin, N. E. 1985 Generation of periodic trains of picosecond pulses in an optical fiber: exact solutions. Sov. Phys. JETP 62 (5), 894–899.Google Scholar
Alberello, A., Chabchoub, A., Monty, J. P., Nelli, F., Lee, J. H., Elsnab, J. & Toffoli, A. 2018 An experimental comparison of velocities underneath focussed breaking waves. Ocean Engng 155, 201–210.CrossRefGoogle Scholar
Babanin, A. 2011 Breaking and Dissipation of Ocean Surface Waves. Cambridge University Press.CrossRefGoogle Scholar
Baldock, T. E., Swan, C. & Taylor, P. H. 1996 A laboratory study of nonlinear surface waves on water. Phil. Trans. R. Soc. Lond. A 354 (1707), 649–676.Google Scholar
Carminati, R., Pierrat, R., De Rosny, J. & Fink, M. 2007 Theory of the time reversal cavity for electromagnetic fields. Opt. Lett. 32 (21), 3107–3109.CrossRefGoogle ScholarPubMed
Chabchoub, A. & Fink, M. 2014 Time-reversal generation of rogue waves. Phys. Rev. Lett. 112, 124101.CrossRefGoogle ScholarPubMed
Chabchoub, A., Onorato, M. & Akhmediev, N. 2016 Hydrodynamic envelope solitons and breathers. In Rogue and Shock Waves in Nonlinear Dispersive Media, pp. 55–87. Springer.CrossRefGoogle Scholar
Chaplin, J. R. 1996 On frequency-focusing unidirectional waves. Intl J. Offshore Polar Engng 6 (2), 131–137.Google Scholar
Clauss, G. F. & Klein, M. 2011 The new year wave in a seakeeping basin: generation, propagation, kinematics and dynamics. Ocean Engng 38 (14–15), 1624–1639.CrossRefGoogle Scholar
Clauss, G. & Schmittner, C. 2007 Experimental optimization of extreme wave sequences for the deterministic analysis of wave/structure interaction. J. Offshore Mech. Arctic Engng 129, 61–67.CrossRefGoogle Scholar
Cousins, W. & Sapsis, T. P. 2016 Reduced-order precursors of rare events in unidirectional nonlinear water waves. J. Fluid Mech. 790, 368–388.CrossRefGoogle Scholar
Dalzell, J. F. 1999 A note on finite depth second-order wave–wave interactions. Appl. Ocean Res. 21 (3), 105–111.CrossRefGoogle Scholar
Dean, R. G. & Dalrymple, R. A. 1991 Water Wave Mechanics for Engineers and Scientists, vol. 2. World Scientific.CrossRefGoogle Scholar
Ducrozet, G., Bonnefoy, F. & Ferrant, P. 2016a On the equivalence of unidirectional rogue waves detected in periodic simulations and reproduced in numerical wave tanks. Ocean Engng 117, 346–358.CrossRefGoogle Scholar
Ducrozet, G., Bonnefoy, F., Le Touzé, D. & Ferrant, P. 2012 A modified high-order spectral method for wavemaker modeling in a numerical wave tank. Eur. J. Mech. (B/Fluids) 34, 19–34.CrossRefGoogle Scholar
Ducrozet, G., Bonnefoy, F. & Perignon, Y. 2017 Applicability and limitations of highly non-linear potential flow solvers in the context of water waves. Ocean Engng 142, 233–244.CrossRefGoogle Scholar
Ducrozet, G., Fink, M. & Chabchoub, A. 2016b Time-reversal of nonlinear waves: applicability and limitations. Phys. Rev. Fluids 1, 054302.CrossRefGoogle Scholar
Dudley, J. M., Genty, G., Mussot, A., Chabchoub, A. & Dias, F. 2019 Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 1, 675–689.CrossRefGoogle Scholar
Fedele, F., Brennan, J., De León, S. P., Dudley, J. & Dias, F. 2016 Real world ocean rogue waves explained without the modulational instability. Sci. Rep. 6, 27715.CrossRefGoogle ScholarPubMed
Fernandez, H., Sriram, V., Schimmels, S. & Oumeraci, H. 2014 Extreme wave generation using self correcting method – revisited. Coast. Engng 93 (0), 15–31.CrossRefGoogle Scholar
Fink, M. 1992 Time reversal of ultrasonic fields. Part I. Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 39 (5), 555–566.CrossRefGoogle Scholar
Fink, M. 1999 Time-reversed acoustics. Sci. Am. 281 (5), 91–97.CrossRefGoogle Scholar
Fouque, J.-P. & Nachbin, A. 2003 Time-reversed refocusing of surface water waves. Multiscale Model. Simul. 1 (4), 609–629.CrossRefGoogle Scholar
Fujimoto, W., Waseda, T. & Webb, A. 2019 Impact of the four-wave quasi-resonance on freak wave shapes in the ocean. Ocean Dyn. 69 (1), 101–121.CrossRefGoogle Scholar
Grue, J. & Jensen, A. 2006 Experimental velocities and accelerations in very steep wave events in deep water. Eur. J. Mech. (B/Fluids) 25 (5), 554–564.CrossRefGoogle Scholar
Haver, S. 2004 A possible freak wave event measured at the Draupner Jacket January 1 1995. In Proceedings of Rogue Waves 2004. IFREMER.Google Scholar
Haver, S., Eik, K. J. & Meling, T. S.2002 On the prediction of wave crest height extremes. Tech. Rep. Statoil.Google Scholar
Kharif, C., Pelinovsky, E. & Slunyaev, A. 2009 Rogue waves in the ocean, observation, theories and modeling. In Advances in Geophysical and Environmental Mechanics and Mathematics Series. Springer.Google Scholar
Liu, P. C. & Mori, N. 2001 Characterizing freak waves with wavelet transform analysis. In Proceedings of Rogue Waves 2000 Workshop, pp. 151–156. IFREMER.Google Scholar
McAllister, M. L., Draycott, S., Adcock, T. A. A., Taylor, P. H. & Van Den Bremer, T. S. 2019 Laboratory recreation of the draupner wave and the role of breaking in crossing seas. J. Fluid Mech. 860, 767–786.CrossRefGoogle Scholar
de Mello, P. C., Pérez, N., Adamowski, J. C. & Nishimoto, K. 2016 Wave focalization in a wave tank by using time reversal technique. Ocean Engng 123, 314–326.CrossRefGoogle Scholar
Mori, N., Liu, P. & Yasuda, T. 2002 Analysis of freak wave measurements in the Sea of Japan. Ocean Engng 29, 1399–1414.CrossRefGoogle Scholar
Mori, N., Onorato, M. & Janssen, P. A. E. M. 2011 On the estimation of kurtosis in directional sea states for freak waves forecasting. J. Phys. Oceanogr. 41, 1484–1496.CrossRefGoogle Scholar
Onorato, M., Residori, S., Bortolozzo, U., Montina, A. & Arecchi, F. T. 2013 Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 528 (2), 47–89.CrossRefGoogle Scholar
Onorato, M., Waseda, T., Toffoli, A., Cavaleri, L., Gramstad, O., Janssen, P. A. E. M., Kinoshita, T., Monbaliu, J., Mori, N., Osborne, A. R. et al. 2009 Statistical properties of directional ocean waves: the role of the modulational instability in the formation of extreme events. Phys. Rev. Lett. 102 (11), 114502.CrossRefGoogle ScholarPubMed
Peregrine, D. H. 1983 Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 25 (1), 16–43.Google Scholar
Przadka, A., Feat, S., Petitjeans, P., Pagneux, V., Maurel, A. & Fink, M. 2012 Time reversal of water waves. Phys. Rev. Lett. 109, 064501.CrossRefGoogle ScholarPubMed
Schäffer, H. A. 1996 Second-order wavemaker theory for irregular waves. Ocean Engng 23 (1), 47–88.CrossRefGoogle Scholar
Schmittner, C., Kosleck, S. & Hennig, J. 2009 A phase-amplitude iteration scheme for the optimization of deterministic wave sequences. In Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering, pp. 653–660. ASME.Google Scholar
Shemer, L., Goulitski, K. & Kit, E. 2007 Evolution of wide-spectrum unidirectional wave groups in a tank: an experimental and numerical study. Eur. J. Mech. (B/Fluids) 26 (2), 193–219.CrossRefGoogle Scholar
Shrira, V. I. & Geogjaev, V. V. 2010 What makes the peregrine soliton so special as a prototype of freak waves? J. Engng Maths 67 (1–2), 11–22.CrossRefGoogle Scholar
Tromans, P. S., Anaturk, A. R. & Hagemeijer, P. 1991 A new model for the kinematics of large ocean waves – application as a design wave. In Proceedings of the 1st International Offshore and Polar Engineering Conference, pp. 64–71. International Society of Offshore and Polar Engineers.Google Scholar
Yasuda, T., Mori, N., Nakayama, S. et al. 1994 Freak wave kinematics in unidirectional deep water waves. In Proceedings of the 4th International Offshore and Polar Engineering Conference, pp. 43–50. International Society of Offshore and Polar Engineers.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.CrossRefGoogle Scholar