Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-21T08:19:09.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental and numerical studies of magnetoconvection in a rapidly rotating spherical shell

Published online by Cambridge University Press:  21 May 2007

N. GILLET ,
D. BRITO ,
D. JAULT  and
H. C. NATAF
N. GILLET
Affiliation:
Laboratoire de Géeophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
D. BRITO
Affiliation:
Laboratoire de Géeophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
D. JAULT
Affiliation:
Laboratoire de Géeophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
H. C. NATAF
Affiliation:
Laboratoire de Géeophysique Interne et Tectonophysique, CNRS, Observatoire de Grenoble, Université Joseph–Fourier, Maison des Géosciences, BP 53, 38041 Grenoble Cedex 09, France
Get access Rights & Permissions [Opens in a new window]

Abstract

Thermal magnetoconvection in a rapidly rotating spherical shell is investigated numerically and experimentally in electrically conductive liquid gallium (Prandtl number P = 0.025), at Rayleigh numbers R up to around 6 times critical and at Ekman numbers E ∼ 10−6. This work follows up the non-magnetic study of convection presented in a companion paper (Gillet et al. 2007). We study here the addition of a z-invariant toroidal magnetic field to the fluid flow. The experimental measurements of fluid velocities by ultrasonic Doppler velocimetry, together with the quasi-geostrophic numerical simulations incorporating a three-dimensional modelling of the magnetic induction processes, demonstrate a stabilizing effect of the magnetic field in the weak-field case, characterized by an Elsasser number Λ < (E/P)1/3. We find that this is explained by the changes of the critical parameters at the onset of convection as Λ increases. As in the non-magnetic study, strong zonal jets of characteristic length scales ℓβ (Rhines length scale) dominates the fluid dynamics. A new characteristic of the magnetoconvective flow is the elongation of the convective cells in the direction of the imposed magnetic field, introducing a new length scale ℓφ. 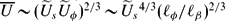Combining experimental and numerical results, we derive a scaling law where U is the axisymmetric motion amplitude, Ũs and Ũφ are the non-axisymmetric radial and azimuthal motion amplitudes, respectively.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 580 , 10 June 2007 , pp. 123 - 143
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aubert, J. 2005 Steady zonal flows in spherical shell fluid dynamos. J. Fluid Mech. 542, 53–67.CrossRefGoogle Scholar
Aubert, J., Brito, D., Nataf, H.-C., Cardin, P. & Masson, J. 2001 A systematic experimental study of rapidly rotating spherical convection in water and liquid gallium. Phys. Earth Planet. Inter. 128, 51–74.CrossRefGoogle Scholar
Aurnou, J. M. & Olson, P. L. 2001 Experiments on Rayleigh-Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.CrossRefGoogle Scholar
Brito, D. 1998 Approches expérimentales et théoriques de la dynamique du noyau terrestre. PhD thesis, Université Paris VII.Google Scholar
Brito, D., Cardin, P., Nataf, H.-C. & Marolleau, G. 1995 Experimental study of a geostrophic vortex of gallium in a transverse magnetic field. Phys. Earth Planet. Inter. 91, 77–98.CrossRefGoogle Scholar
Brito, D., Cardin, P., Nataf, H.-C. & Olson, P. 1996 Experiments on Joule heating and the dissipation of energy in the Earth's core. Geophys. J. Intl 127, 339–347.CrossRefGoogle Scholar
Brito, D., Nataf, H.-C., Cardin, P., Aubert, J. & Masson, J. 2001 Ultrasonic Doppler velocimetry in liquid gallium. Exps. Fluids 31, 653–663.CrossRefGoogle Scholar
Busse, F. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44, 441–460.CrossRefGoogle Scholar
Busse, F. H. & Finocchi, F. 1993 The onset of thermal convection in a rotating cylindrical annulus in the presence of a magnetic field. Phys. Earth Planet. Inter. 80, 13–23.CrossRefGoogle Scholar
Cardin, P. & Olson, P. 1995 The influence of a toroidal magnetic field on thermal convection in the core. Earth Planet. Sci. Lett. 132, 167–181.CrossRefGoogle Scholar
Chandrasekar, S. 1954 The instability of a layer of fluid heated bellow and subject to the simultaneous action of a magnetic field and rotation. Proc. R. Soc. Lond. A 225, 173–184.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166, 97–114.CrossRefGoogle Scholar
Dumberry, M. & Bloxham, J. 2003 Torque balance, Taylor's constraint and torsional oscillations in a numerical model of the geodynamo. Phys. Earth Planet. Int. 140, 29–51.CrossRefGoogle Scholar
Fearn, D. R. 1979 a Thermal and magnetic instabilities in a rapidly rotating sphere. Geophys. Astrophys. Fluid Dyn. 14, 103–126.CrossRefGoogle Scholar
Fearn, D. R. 1979 b Thermally driven hydromagnetic convection in a rapidly rotating sphere. Proc. R. Soc. Lond. A 369, 227–242.Google Scholar
Fearn, D. R. & Rahman, M. M. 2004 The role of inertia in models of the geodynamo. Geophys. J. Intl 158, 515–528.CrossRefGoogle Scholar
Galperin, B., Nakano, H., Huang, H.-P. & Sukoriansky, S. 2004 The ubiquitous zonal jets in the atmospheres of giant planets and Earth's ocean. Geophys. Res. Lett. 31, doi:10.1029/ 2004GL019691.CrossRefGoogle Scholar
Gillet, N. 2004 Magnéto-convection dans une sphère en rotation rapide: approches experimentale et numérique de la convection dans les noyaux planetaires. PhD thesis, Université Joseph-Fourier (Grenoble I).Google Scholar
Gillet, N., Brito, D., Jault, D. & Nataf, H.-C. 2007 Experimental and numerical studies of convection in a rapidly rotating spherical shell. J. Fluid Mech. 580, 83–121.CrossRefGoogle Scholar
Gillet, N. & Jones, C. A. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.CrossRefGoogle Scholar
Hide, R. 1966 Free hydromagnetic oscillations of the Earth's core and the theory of geomagnetic secular variations. Phil. Trans. R. Soc. Lond. A 259, 615–646.Google Scholar
Jaletzky, M. 1999 Experimental study of rotating cylindrical annulus convection. PhD thesis, University of Bayreuth.Google Scholar
Jones, C. A., Mussa, A. I. & Worland, S. J. 2003 Magnetoconvection in a rapidly rotating sphere: the weak-field case. Proc. R. Soc. Lond. A 459, 773–797.CrossRefGoogle Scholar
Nagakawa, Y. 1957 Experiments on the instability of a plane layer of mercury heated from below and subject to the simultaneous action of a magnetic field and rotation. Proc. R. Soc. Lond. A 242, 81–88.Google Scholar
Nagakawa, Y. 1958 Experiments on the instability of a plane layer of mercury heated from below and subject to the simultaneous action of a magnetic field and rotation. II. Proc. R. Soc. Lond. A 249, 138–145.Google Scholar
Olson, P. & Glatzmaier, G. 1995 Magnetoconvection in a rotating spherical shell: structure of the flow in the outer core. Phys. Earth Planet. Inter. 92, 109–118.CrossRefGoogle Scholar
Or, A. C. & Busse, F. 1987 Convection in a rotating cylindrical annulus. Part 2. Transitions to asymmetric and vacillating flow. J. Fluid Mech. 174, 313–326.CrossRefGoogle Scholar
Petry, M., Busse, F. & Finocchi, F. 1997 Convection in a rotating cylindrical annulus in the presence of a magnetic field. Eur. J. Mech. BFluids 16 (6), 817–833.Google Scholar
Read, P. L., Yamazaki, Y. H., Lewis, S. R., Williams, P. D., Miki-Yamazaki, K., Sommeria, J., Didelle, H. & Fincham, A. 2004 Jupiter's and Saturn's convectively driven banded jets in the laboratory. Geophys. Res. Lett. 31, 22701 CrossRefGoogle Scholar
Rhines, P. B. 1975 Wave and turbulence on a beta-plane. J. Fluid Mech. 122, 417–443.CrossRefGoogle Scholar
Roberts, P. H. 1968 On the thermal instability of a self-graviting fluid sphere containing heat sources. Phil. Trans. R. Soc. Lond. A 263, 93–117.Google Scholar
Schnaubelt, M. & Busse, F. H. 1992 Convection in a rotating cylindrical annulus. Part 3. Vacillating and spatially modulated flows. J. Fluid Mech. 245, 155–173.CrossRefGoogle Scholar
Secco, R. A. & Schloessin, H. H. 1989 The electrical resistivity of solid and liquid Fe at pressures up to 7 GPa. J. Geophy. Res. 94, 5887–5894.CrossRefGoogle Scholar
Shew, W. & Lathrop, D. P. 2005 Liquid sodium model of geophysical core convection. Phys. Earth Planet. Inter. 153, 136–149.CrossRefGoogle Scholar
Soward, A. 1979 Convection driven dynamos. Phys. Earth Planet. Inter. 20, 134–151.CrossRefGoogle Scholar
Wijs, G. D., Kresse, G., Vocadlo, L., Dobson, D., Alfè, D., Gillan, M. J. & Price, G. D. 1998 The viscosity of liquid iron at the physical conditions of the earth's core. Nature 392, 805–807.CrossRefGoogle Scholar
Zhang, K. 1999 Nonlinear magnetohydrodynamic convective flows in the Earth's fluid core. Phys. Earth Planet. Inter. 111, 93–105.CrossRefGoogle Scholar
Zhang, K., Weels, M. & Roberts, P. 2004 Effect of electrically conducting walls on rotating magnetoconvection. Phys. Fluids 16, 2023–2032.CrossRefGoogle Scholar