Published online by Cambridge University Press: 30 August 2016
In this paper, we investigate the elliptical instability exhibited by two counter-rotating trailing vortices. This type of instability can be viewed as a resonance between two normal modes of a vortex and an external strain field. Recent numerical investigations have extended earlier results that ignored axial flow to include models with a simple wake-like axial flow such as the similarity solution found by Batchelor (J. Fluid Mech., vol. 20, 1964, pp. 645–658). We present herein growth rates of elliptical instability for a family of velocity profiles found by Moore & Saffman (Proc. R. Soc. Lond. A, vol. 333, 1973, pp. 491–508). These profiles have a parameter  $n$ that depends on the wing loading. As a result, unlike the Batchelor vortex, they are capable of modelling both the jet-like and the wake-like axial flow present in a trailing vortex at short and intermediate distances behind a wingtip. Direct numerical simulations of the linearized Navier–Stokes equations are performed using an efficient spectral method in cylindrical coordinates developed by Matsushima & Marcus (J. Comput. Phys., vol. 53, 1997, pp. 321–345). We compare our results with those for the Batchelor vortex, whose velocity profiles are closely approximated as the wing loading parameter
$n$ that depends on the wing loading. As a result, unlike the Batchelor vortex, they are capable of modelling both the jet-like and the wake-like axial flow present in a trailing vortex at short and intermediate distances behind a wingtip. Direct numerical simulations of the linearized Navier–Stokes equations are performed using an efficient spectral method in cylindrical coordinates developed by Matsushima & Marcus (J. Comput. Phys., vol. 53, 1997, pp. 321–345). We compare our results with those for the Batchelor vortex, whose velocity profiles are closely approximated as the wing loading parameter  $n$ approaches 1. An important conclusion of our investigation is that the stability characteristics vary considerably with
$n$ approaches 1. An important conclusion of our investigation is that the stability characteristics vary considerably with  $n$ and
$n$ and 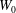 $W_{0}$, a parameter measuring the strength of the mean axial velocity component. In the case of an elliptically loaded wing (
$W_{0}$, a parameter measuring the strength of the mean axial velocity component. In the case of an elliptically loaded wing (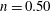 $n=0.50$), we find that the instability growth rates are up to 50 % greater than those for the Batchelor vortex. Our results demonstrate the significant effect of the distribution and intensity of the axial flow on the elliptical instability of a trailing vortex.
$n=0.50$), we find that the instability growth rates are up to 50 % greater than those for the Batchelor vortex. Our results demonstrate the significant effect of the distribution and intensity of the axial flow on the elliptical instability of a trailing vortex.