Published online by Cambridge University Press: 31 August 2016
The influence of a multi-scale fractal based geometry on the decay of turbulence is investigated by comparing the turbulence produced by a square fractal element grid to that produced by two regular grids with similar physical properties. Comparison of the grid wakes at constant grid Reynolds number, 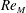 $Re_{M}$, identifies that in the far field both regular grids produce comparable or higher turbulence intensities and local Reynolds numbers,
$Re_{M}$, identifies that in the far field both regular grids produce comparable or higher turbulence intensities and local Reynolds numbers, 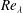 $Re_{\unicode[STIX]{x1D706}}$, than the square fractal element grid. This result is illustrative of a limitation of multi-scale geometries to produce the oft-quoted high levels of turbulence intensity and
$Re_{\unicode[STIX]{x1D706}}$, than the square fractal element grid. This result is illustrative of a limitation of multi-scale geometries to produce the oft-quoted high levels of turbulence intensity and 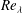 $Re_{\unicode[STIX]{x1D706}}$. In the far field, the spectra are approximately collapsed at all scales for all three grids at a given
$Re_{\unicode[STIX]{x1D706}}$. In the far field, the spectra are approximately collapsed at all scales for all three grids at a given 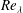 $Re_{\unicode[STIX]{x1D706}}$. When a non-equilibrium near field spectrum with
$Re_{\unicode[STIX]{x1D706}}$. When a non-equilibrium near field spectrum with 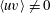 $\langle uv\rangle \neq 0$ is compared to a far field spectrum at the same
$\langle uv\rangle \neq 0$ is compared to a far field spectrum at the same 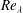 $Re_{\unicode[STIX]{x1D706}}$ but with
$Re_{\unicode[STIX]{x1D706}}$ but with 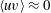 $\langle uv\rangle \approx 0$, it is shown that their shapes are markedly different and that the non-equilibrium spectrum has a steeper slope, giving the appearance of being nearer
$\langle uv\rangle \approx 0$, it is shown that their shapes are markedly different and that the non-equilibrium spectrum has a steeper slope, giving the appearance of being nearer 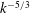 $k^{-5/3}$, although there is no theoretical expectation of an inertial range at such locations in the flow. However, when a non-equilibrium spectrum with
$k^{-5/3}$, although there is no theoretical expectation of an inertial range at such locations in the flow. However, when a non-equilibrium spectrum with 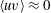 $\langle uv\rangle \approx 0$ is compared to a far field spectrum at the same
$\langle uv\rangle \approx 0$ is compared to a far field spectrum at the same 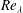 $Re_{\unicode[STIX]{x1D706}}$, they are once again collapsed. This is shown to be related to non-zero Reynolds shear stress at scales that penetrate the scaling range for the present experiment, and hence the influence of shear is not limited to the largest scales. These results demonstrate the importance of local properties of the flow on the turbulence spectra at given locations in the inherently inhomogeneous flow found in the non-equilibrium region downstream of grids. In particular, how the presence of local shear stress can fundamentally change the shape of the spectra at scales that can be mistakenly interpreted as an inertial range.
$Re_{\unicode[STIX]{x1D706}}$, they are once again collapsed. This is shown to be related to non-zero Reynolds shear stress at scales that penetrate the scaling range for the present experiment, and hence the influence of shear is not limited to the largest scales. These results demonstrate the importance of local properties of the flow on the turbulence spectra at given locations in the inherently inhomogeneous flow found in the non-equilibrium region downstream of grids. In particular, how the presence of local shear stress can fundamentally change the shape of the spectra at scales that can be mistakenly interpreted as an inertial range.