Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-19T15:07:59.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Dewetting acceleration by evaporation

Published online by Cambridge University Press:  16 September 2022

Xiaolong Zhang Open the ORCID record for Xiaolong Zhang [Opens in a new window]  and
Vadim S. Nikolayev Open the ORCID record for Vadim S. Nikolayev [Opens in a new window]
Xiaolong Zhang
Affiliation:
Service de Physique de l'Etat Condensé, CEA, CNRS, Université Paris-Saclay, 91191 Gif-sur-Yvette Cedex, France
Vadim S. Nikolayev*
Affiliation:
Service de Physique de l'Etat Condensé, CEA, CNRS, Université Paris-Saclay, 91191 Gif-sur-Yvette Cedex, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

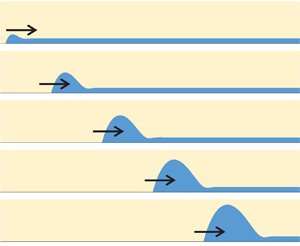
Dewetting of a substrate, i.e. the liquid film retraction under partial wetting conditions, has been studied extensively over the past decades. This theoretical work deals with the dewetting phenomenon in the presence of liquid evaporation into the pure vapour atmosphere driven by substrate superheating with respect to the saturation temperature corresponding to the vapour pressure. The dynamic profile of the vapour–liquid interface is analysed numerically by using the generalised lubrication approximation that can be applied to an interface slope larger than its conventional counterpart. This approximation uses a phenomenological argument to increase the precision of calculations. For small slopes, it reduces to the conventional lubrication approach. Several nanoscale effects are included in the theory to obtain more precise results: the Kelvin effect, the hydrodynamic slip, the Marangoni effect, the vapour recoil and the interfacial thermal resistance. Their relative importance is discussed. The results include the film shape evolution, the apparent contact angle and the contact line speed, all defined by the substrate superheating and its wetting properties. These dependencies agree with existing experimental results. It is found that the dewetting is accelerated by evaporation. The numerical results are compared to those of the multiscale theory that uses two main parameters, the Voinov angle (the apparent angle obtained within the microregion problem) and the Voinov length. The latter is studied for several fluids as a function of superheating, and an approximate expression for it is proposed. A good agreement between the numerics and the multiscale theory shows the validity of the latter. This means that the dewetting speed in the presence of evaporation can be calculated with an analytical expression that requires only the Voinov angle as a numerical input. Such results are important for many applications, for instance, bubble growth in boiling or film dynamics in heat pipes.

JFM classification

Interfacial Flows (free surface): Contact lines Low-Reynolds-number flows: Lubrication theory Phase change: Condensation/evaporation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 948 , 10 October 2022 , A49
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, D.M., Cermelli, P., Fried, E., Gurtin, M.E. & McFadden, G.B. 2007 General dynamical sharp-interface conditions for phase transformations in viscous heat-conducting fluids. J. Fluid Mech. 581, 323–370.CrossRefGoogle Scholar
Anderson, D.M. & Davis, S.H. 1994 Local fluid and heat flow near contact lines. J. Fluid Mech. 268, 231–265.CrossRefGoogle Scholar
Anderson, D.M. & Janeček, V. 2018 Comment on L. M. Hocking, ‘On contact angles in evaporating liquids’ [Phys. Fluids 7, 2950–2955 (1995)]. Phys. Fluids 30 (7), 079101.CrossRefGoogle Scholar
Boender, W., Chesters, A.K. & van der Zanden, A.J.J. 1991 An approximate analytical solution of the hydrodynamic problem associated with an advancing liquid–gas contact line. Int. J. Multiphase Flow 17, 661–676.CrossRefGoogle Scholar
Brochard-Wyart, F., Di Meglio, J.-M., Quere, D. & de Gennes, P.-G. 1991 Spreading of nonvolatile liquids in a continuum picture. Langmuir 7 (2), 335–338.CrossRefGoogle Scholar
Bureš, L. & Sato, Y. 2021 On the modelling of the transition between contact-line and microlayer evaporation regimes in nucleate boiling. J. Fluid Mech. 916, A53.CrossRefGoogle Scholar
Chan, T.S., Kamal, C., Snoeijer, J.H., Sprittles, J.E. & Eggers, J. 2020 Cox–Voinov theory with slip. J. Fluid Mech. 900, A8.CrossRefGoogle Scholar
Chan, T.S., Srivastava, S., Marchand, A., Andreotti, B., Biferale, L., Toschi, F. & Snoeijer, J.H. 2013 Hydrodynamics of air entrainment by moving contact lines. Phys. Fluids 25 (7), 074105.CrossRefGoogle Scholar
Cox, R.G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.CrossRefGoogle Scholar
Delon, G., Fermigier, M., Snoeijer, J.H. & Andreotti, B. 2008 Relaxation of a dewetting contact line. Part 2: Experiments. J. Fluid Mech. 604, 55–75.Google Scholar
Edwards, A.M.J., Ledesma-Aguilar, R., Newton, M.I., Brown, C.V. & McHale, G. 2016 Not spreading in reverse: the dewetting of a liquid film into a single drop. Sci. Adv. 2 (9), e1600183.CrossRefGoogle ScholarPubMed
Fourgeaud, L., Ercolani, E., Duplat, J., Gully, P. & Nikolayev, V.S. 2016 Evaporation-driven dewetting of a liquid film. Phys. Rev. Fluids 1 (4), 041901.CrossRefGoogle Scholar
de Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.CrossRefGoogle Scholar
Hocking, L.M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mechanics Appl. Math. 36 (1), 55–69.CrossRefGoogle Scholar
Hocking, L.M. 1995 On contact angles in evaporating liquids. Phys. Fluids 7, 2950–2955.CrossRefGoogle Scholar
Janeček, V., Andreotti, B., Pražák, D., Bárta, T. & Nikolayev, V.S. 2013 Moving contact line of a volatile fluid. Phys. Rev. E 88 (6), 060404.CrossRefGoogle ScholarPubMed
Janeček, V. & Nikolayev, V.S. 2012 Contact line singularity at partial wetting during evaporation driven by substrate heating. Europhys. Lett. 100 (1), 14003.CrossRefGoogle Scholar
Janeček, V. & Nikolayev, V.S. 2014 Triggering the boiling crisis: a study of the dry spot spreading mechanism. Interfacial Phenom. Heat Transf. 2 (4), 363–383.CrossRefGoogle Scholar
Lauga, E., Brenner, M.P. & Stone, H.A. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Dynamics (ed. C. Tropea, A. Yarin & J. Foss), chap. 19, pp. 1217–1240. Springer.CrossRefGoogle Scholar
Mathieu, B. 2003 Etudes physiques, expérimentale et numérique des mécanismes de base intervenant dans les écoulements diphasiques. PhD thesis, Polytech Marseille, Université de Provence.Google Scholar
Moffatt, H.K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.CrossRefGoogle Scholar
Nikolayev, V.S. 2010 Dynamics of the triple contact line on a nonisothermal heater at partial wetting. Phys. Fluids 22 (8), 082105.CrossRefGoogle Scholar
Nikolayev, V.S. 2021 Physical principles and state-of-the-art of modeling of the pulsating heat pipe: a review. Appl. Therm. Eng. 195, 117111.CrossRefGoogle Scholar
Nikolayev, V.S. 2022 Evaporation effect on the contact angle and contact line dynamics. In The Surface Wettability Effect on Phase Change (ed. M. Marengo & J.D. Coninck), chap. 6, pp. 133–187. Springer.CrossRefGoogle Scholar
Nikolayev, V.S. & Beysens, D.A. 1999 Boiling crisis and non-equilibrium drying transition. Europhys. Lett. 47 (3), 345–351.CrossRefGoogle Scholar
Rednikov, A. & Colinet, P. 2013 Singularity-free description of moving contact lines for volatile liquids. Phys. Rev. E 87 (1), 010401.CrossRefGoogle ScholarPubMed
Saxton, M.A., Vella, D., Whiteley, J.P. & Oliver, J.M. 2017 Kinetic effects regularize the mass-flux singularity at the contact line of a thin evaporating drop. J. Eng. Math. 106 (1), 47–73.CrossRefGoogle ScholarPubMed
Snoeijer, J.H. 2006 Free-surface flows with large slopes: beyond lubrication theory. Phys. Fluids 18, 021701.CrossRefGoogle Scholar
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45 (1), 269–292.CrossRefGoogle Scholar
Snoeijer, J.H. & Eggers, J. 2010 Asymptotic analysis of the dewetting rim. Phys. Rev. E 82 (5), 056314.CrossRefGoogle ScholarPubMed
Tecchio, C., Zhang, X., Cariteau, B., Zalczer, G., Roca i Cabarrocas, P., Bulkin, P., Charliac, J., Vassant, S. & Nikolayev, V. 2022 Microlayer dynamics at bubble growth in boiling. In Proc. 16th Int. Conf. Heat Transfer Fluid Mech. Thermodynamics (HEFAT-ATE 2022), pp. 624-629.Google Scholar
Urbano, A., Tanguy, S., Huber, G. & Colin, C. 2018 Direct numerical simulation of nucleate boiling in micro-layer regime. Int. J. Heat Mass Transfer 123, 1128–1137.CrossRefGoogle Scholar
Voinov, O. 1976 Hydrodynamics of wetting. Fluid Dyn. 11 (5), 714–721.CrossRefGoogle Scholar
Wayner, P.C. 1993 Spreading of a liquid film with a finite contact angle by the evaporation/condensation process. Langmuir 9 (1), 294–299.CrossRefGoogle Scholar
Zhang, X. & Nikolayev, V.S. 2021 Liquid film dynamics with immobile contact line during meniscus oscillation. J. Fluid Mech. 923, A4.CrossRefGoogle Scholar

Zhang and Nikolayev Supplementary Movie

Dynamics of adiabatic dewetting for the same parameters as in figure 4.

Download Zhang and Nikolayev Supplementary Movie(Video)
Video 741.5 KB