Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Shizhao
He, Guowei
and
Zhang, Xing
2015.
Lift enhancement on spanwise oscillating flat-plates in low-Reynolds-number flows.
Physics of Fluids,
Vol. 27,
Issue. 6,
Siala, Firas F.
Totpal, Alexander D.
and
Liburdy, James A.
2016.
Characterization of Vortex Dynamics in the Near Wake of an Oscillating Flexible Foil.
Journal of Fluids Engineering,
Vol. 138,
Issue. 10,
laBastide, B. P.
Wong, J. G.
and
Rival, D. E.
2016.
Wind Shear, Gust, and Yaw-Induced Dynamic Stall on Wind-Turbine Blades.
Journal of Physics: Conference Series,
Vol. 753,
Issue. ,
p.
032023.
Medina, Albert
and
Jones, Anya R.
2016.
Leading-edge vortex burst on a low-aspect-ratio rotating flat plate.
Physical Review Fluids,
Vol. 1,
Issue. 4,
Ehlers, Hauke
Konrath, Robert
Wokoeck, Ralf
and
Radespiel, Rolf
2016.
Three-Dimensional Flow Field Investigations of Flapping Wing Aerodynamics.
AIAA Journal,
Vol. 54,
Issue. 11,
p.
3434.
Jones, Anya R.
Medina, Albert
Spooner, Hannah
and
Mulleners, Karen
2016.
Characterizing a burst leading-edge vortex on a rotating flat plate wing.
Experiments in Fluids,
Vol. 57,
Issue. 4,
Wong, Jaime G.
and
Rival, David E.
2017.
Rapid manoeuvring with spanwise-flexible wings.
Journal of Fluids and Structures,
Vol. 75,
Issue. ,
p.
1.
Wong, J G
laBastide, B P
and
Rival, D E
2017.
Flow separation on flapping and rotating profiles with spanwise gradients.
Bioinspiration & Biomimetics,
Vol. 12,
Issue. 2,
p.
026008.
Onoue, Kyohei
and
Breuer, Kenneth S.
2017.
A scaling for vortex formation on swept and unswept pitching wings.
Journal of Fluid Mechanics,
Vol. 832,
Issue. ,
p.
697.
Wong, Jaime G.
Gillespie, Graeme
and
Rival, David E.
2018.
Circulation Redistribution in Leading-Edge Vortices with Spanwise Flow.
AIAA Journal,
Vol. 56,
Issue. 10,
p.
3857.
Chen, Long
Wu, Jianghao
and
Cheng, Bo
2019.
Volumetric measurement and vorticity dynamics of leading-edge vortex formation on a revolving wing.
Experiments in Fluids,
Vol. 60,
Issue. 1,
Chowdhury, Juhi
Cook, Luke
and
Ringuette, Matthew J.
2019.
The Vortex Formation of an Unsteady Translating Plate with a Rotating Tip.
Smith, Luke R.
Jung, Yong Su
Baeder, James D.
and
Jones, Anya R.
2019.
The role of rotary motion on vortices in reverse flow.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
723.
Scofield, Tyler
Jia, Kun
Wei, Mingjun
and
Bhattacharya, Samik
2019.
Vorticity-Transfer in a Leading-Edge-Vortex due to Controlled Spanwise-Bending.
Kissing, Johannes
Kriegseis, Jochen
Li, Zhenyao
Feng, Lihao
Hussong, Jeanette
and
Tropea, Cameron
2020.
Insights into leading edge vortex formation and detachment on a pitching and plunging flat plate.
Experiments in Fluids,
Vol. 61,
Issue. 9,
Joshi, Kamlesh
Vazquez, Christian G.
Kauffman, Jeffrey L.
and
Bhattacharya, Samik
2020.
Unsteady Maneuvering of a Morphing Wing.
Zhang, Jiao-Long
Jun-Hu
Yu, Yong
and
Xuan, Hai-Bin
2020.
The influence of leading-edge deflection on the stability of the leading-edge vortices.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 234,
Issue. 20,
p.
3992.
Smith, Luke R.
and
Jones, Anya R.
2020.
Vortex formation on a pitching aerofoil at high surging amplitudes.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Smith, Luke
and
Jones, Anya R.
2020.
Unsteady Vortex Formation on Airfoils with High Surging and Pitching Amplitudes.
Kaiser, Frieder
Kriegseis, Jochen
and
Rival, David E.
2020.
The influence of edge undulation on vortex formation for low-aspect-ratio propulsors.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
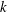 $k$
and profile sweep
$k$
and profile sweep
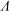 ${\it\Lambda}$
are critical in predicting relative LEV stability as determined by the aforementioned effects. These hypotheses are then confirmed experimentally with phase-averaged particle image velocimetry (PIV) and three-dimensional particle tracking velocimetry. In particular, more stable LEVs are observed at higher reduced frequencies, which is argued to represent the ratio between the limiting vortex size and the rate of vorticity feeding. The introduction of profile sweep increased both relative LEV stability and spanwise vorticity transport. It is thought that spanwise vorticity transport improved LEV stability by acting as a sink for vorticity generated in the leading-edge shear layer.
${\it\Lambda}$
are critical in predicting relative LEV stability as determined by the aforementioned effects. These hypotheses are then confirmed experimentally with phase-averaged particle image velocimetry (PIV) and three-dimensional particle tracking velocimetry. In particular, more stable LEVs are observed at higher reduced frequencies, which is argued to represent the ratio between the limiting vortex size and the rate of vorticity feeding. The introduction of profile sweep increased both relative LEV stability and spanwise vorticity transport. It is thought that spanwise vorticity transport improved LEV stability by acting as a sink for vorticity generated in the leading-edge shear layer.


