Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-19T04:18:51.309Z Has data issue: false hasContentIssue false
  • English
  • Français

The cooling box problem: convection with a quadratic equation of state

Published online by Cambridge University Press:  06 May 2021

Jason Olsthoorn Open the ORCID record for Jason Olsthoorn [Opens in a new window] ,
Edmund W. Tedford  and
Gregory A. Lawrence
Jason Olsthoorn*
Affiliation:
Department of Civil Engineering, University of British Columbia, 2002-6250 Applied Science Lane, Vancouver, BC, CanadaV6T 1Z4
Edmund W. Tedford
Affiliation:
Department of Civil Engineering, University of British Columbia, 2002-6250 Applied Science Lane, Vancouver, BC, CanadaV6T 1Z4
Gregory A. Lawrence
Affiliation:
Department of Civil Engineering, University of British Columbia, 2002-6250 Applied Science Lane, Vancouver, BC, CanadaV6T 1Z4
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

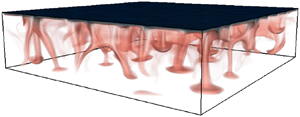
We investigate the convective cooling of a fluid with a quadratic equation of state (EOS) by performing three-dimensional direct numerical simulations of a flow with a fixed top-boundary temperature, which is lower than the initial fluid temperature. We consider fluid temperatures near the density maximum, where the nonlinearity is expected to be important. When the EOS is nonlinear, the resultant vertical transport of heat is fundamentally different and significantly lower than the predictions derived for a linear EOS. Further, three dimensionless groups parameterise the convective system: the Rayleigh number (${Ra}_0$), the Prandtl number (Pr) and the dimensionless bottom water temperature $(T_B)$. We further define an effective Rayleigh number (${Ra}_{eff} = {Ra}_0 \ T_B^2$), which is equivalent to the traditional Rayleigh number used with a linear EOS. We present a predictive model for the vertical heat flux, the top boundary-layer thickness, and the turbulent kinetic energy (TKE) of the system. We show that this model agrees well with the direct numerical simulations. This model could be used to understand how quickly freshwater lakes cool in high-latitude environments.

JFM classification

Convection: Buoyancy-driven instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 918 , 10 July 2021 , A6
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anders, E.H., Vasil, G.M., Brown, B.P. & Korre, L. 2020 Convective dynamics with mixed temperature boundary conditions: why thermal relaxation matters and how to accelerate it. Phys. Rev. Fluids 5 (8), 083501.CrossRefGoogle Scholar
Bars, M.L., Lecoanet, D., Perrard, S., Ribeiro, A., Rodet, L., Aurnou, J.M. & Gal, P.L. 2015 Experimental study of internal wave generation by convection in water. Fluid Dyn. Res. 47 (4), 045502.CrossRefGoogle Scholar
Carmack, E.C. 1979 Combined influence of inflow and lake temperatures on spring circulation in a riverine lake. J. Phys. Oceanogr. 9 (2), 422–434.2.0.CO;2>CrossRefGoogle Scholar
Chen, C.A. & Millero, F.J. 1986 Thermodynamic properties for natural waters covering only the limnological range. Limnol. Oceanogr. 31 (3), 657–662.CrossRefGoogle Scholar
Childs, H., et al. 2012 VisIt: an end-user tool for visualizing and analyzing very large data. In High Performance Visualization – Enabling Extreme-Scale Scientific Insight, pp. 357–372. Taylor & Francis.Google Scholar
Couston, L.A., Lecoanet, D., Favier, B. & Le Bars, M. 2017 Dynamics of mixed convective-stably-stratified fluids. Phys. Rev. Fluids 2 (9), 094804.CrossRefGoogle Scholar
Couston, L.A., Lecoanet, D., Favier, B. & Le Bars, M. 2018 The energy flux spectrum of internal waves generated by turbulent convection. J. Fluid Mech. 854, R3.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge Mathematical Library. Cambridge University Press.CrossRefGoogle Scholar
Farmer, D.M. 1975 Penetrative convection in the absence of mean shear. Q. J. R. Meteorol. Soc. 101 (430), 869–891.CrossRefGoogle Scholar
Farmer, D.M. & Carmack, E. 1981 Wind mixing and restratification in a lake near the temperature of maximum density. J. Phys. Oceanogr. 11 (11), 1516–1533.2.0.CO;2>CrossRefGoogle Scholar
Hay, W.A. & Papalexandris, M.V. 2019 Numerical simulations of turbulent thermal convection with a free-slip upper boundary. Proc. R. Soc. Lond. A 475 (2232), 20190601.Google Scholar
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.CrossRefGoogle Scholar
Kaminski, A.K. & Smyth, W.D. 2019 Stratified shear instability in a field of pre-existing turbulence. J. Fluid Mech. 862, 639–658.CrossRefGoogle Scholar
Kim, J.-H., Moon, W., Wells, A.J., Wilkinson, J.P., Langton, T., Hwang, B., Granskog, M.A. & Rees Jones, D.W. 2018 Salinity control of thermal evolution of late summer melt ponds on arctic sea ice. Geophys. Res. Lett. 45 (16), 8304–8313.CrossRefGoogle Scholar
Lecoanet, D., Le Bars, M., Burns, K.J., Vasil, G.M., Brown, B.P., Quataert, E. & Oishi, J.S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91, 063016.CrossRefGoogle ScholarPubMed
Nijjer, J.S., Hewitt, D.R. & Neufeld, J.A. 2018 The dynamics of miscible viscous fingering from onset to shutdown. J. Fluid Mech. 837, 520–545.CrossRefGoogle Scholar
Olsthoorn, J., Tedford, E.W. & Lawrence, G.A. 2019 Diffused-interface Rayleigh–Taylor instability with a nonlinear equation of state. Phys. Rev. Fluids 4 (9), 1–23.CrossRefGoogle Scholar
Plumley, M. & Julien, K. 2019 Scaling laws in Rayleigh–Bénard convection. Earth Space Sci. 6 (9), 1580–1592.CrossRefGoogle Scholar
Smyth, W.D. & Moum, J.N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.CrossRefGoogle Scholar
Subich, C.J., Lamb, K.G. & Stastna, M. 2013 Simulation of the Navier–Stokes equations in three dimensions with a spectral collocation method. Intl J. Numer. Meth. Fluids 73 (2), 103–129.CrossRefGoogle Scholar
Toppaladoddi, S. & Wettlaufer, J.S. 2017 Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluids 3 (4), 43501.CrossRefGoogle Scholar
Townsend, A.A. 1964 Natural convection in water over an ice surface. Q. J. R. Meteorol. Soc. 90 (385), 248–259.CrossRefGoogle Scholar
Veronis, G. 1963 Penetrative convection. Astrogeophys. J. 137, 641–663.CrossRefGoogle Scholar
Wang, Q., Zhou, Q., Wan, Z.-H. & Sun, D.-J. 2019 Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions. J. Fluid Mech. 870, 718–734.CrossRefGoogle Scholar
Whipple, G.C. 1898 Classification of lakes according to temperature. Am. Nat. 32 (373), 25–33.CrossRefGoogle Scholar