Published online by Cambridge University Press: 25 January 2016
We investigate the fluid mechanics of removing a passive tracer contained in small, thin, viscous drops attached to a flat inclined substrate using thin gravity-driven film flows. We focus on the case where the drop cannot be detached either partially or completely from the surface by the mechanical forces exerted by the cleaning fluid on the drop surface. Instead, a convective mass transfer establishes across the drop–film interface and the dilute passive tracer dispersed in the drop diffuses into the film flow, which then transports them away. The Péclet number for the passive tracer in the film phase is very high, whereas the Péclet number in the drop phase varies from 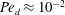 $\mathit{Pe}_{d}\approx 10^{-2}$ to
$\mathit{Pe}_{d}\approx 10^{-2}$ to 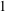 $1$. The characteristic transport time in the drop is much larger than in the film. We model the mass transfer of the passive tracer from the bulk of the drop phase into the film phase using an empirical model based on an analogy with Newton’s law of cooling. This simple empirical model is supported by a theoretical model solving the quasi-steady two-dimensional advection–diffusion equation in the film, coupled with a time-dependent one-dimensional diffusion equation in the drop. We find excellent agreement between our experimental data and the two models, which predict an exponential decrease in time of the tracer concentration in the drop. The results are valid for all drop and film Péclet numbers studied. The overall transport characteristic time is related to the drop diffusion time scale, as diffusion within the drop is the limiting process. This result remains valid even for
$1$. The characteristic transport time in the drop is much larger than in the film. We model the mass transfer of the passive tracer from the bulk of the drop phase into the film phase using an empirical model based on an analogy with Newton’s law of cooling. This simple empirical model is supported by a theoretical model solving the quasi-steady two-dimensional advection–diffusion equation in the film, coupled with a time-dependent one-dimensional diffusion equation in the drop. We find excellent agreement between our experimental data and the two models, which predict an exponential decrease in time of the tracer concentration in the drop. The results are valid for all drop and film Péclet numbers studied. The overall transport characteristic time is related to the drop diffusion time scale, as diffusion within the drop is the limiting process. This result remains valid even for 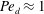 $\mathit{Pe}_{d}\approx 1$. Finally, our theoretical model predicts the well-known relationship between the Sherwood number and the Reynolds number in the case of a well-mixed drop
$\mathit{Pe}_{d}\approx 1$. Finally, our theoretical model predicts the well-known relationship between the Sherwood number and the Reynolds number in the case of a well-mixed drop 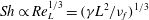 $\mathit{Sh}\propto \mathit{Re}_{L}^{1/3}=({\it\gamma}L^{2}/{\it\nu}_{f})^{1/3}$, based on the drop length
$\mathit{Sh}\propto \mathit{Re}_{L}^{1/3}=({\it\gamma}L^{2}/{\it\nu}_{f})^{1/3}$, based on the drop length 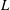 $L$, film shear rate
$L$, film shear rate 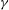 ${\it\gamma}$ and film kinematic viscosity
${\it\gamma}$ and film kinematic viscosity 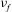 ${\it\nu}_{f}$. We show that this relationship is mathematically equivalent to a more physically intuitive relationship
${\it\nu}_{f}$. We show that this relationship is mathematically equivalent to a more physically intuitive relationship 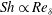 $\mathit{Sh}\propto \mathit{Re}_{{\it\delta}}$, based on the diffusive boundary-layer thickness
$\mathit{Sh}\propto \mathit{Re}_{{\it\delta}}$, based on the diffusive boundary-layer thickness 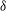 ${\it\delta}$. The model also predicts a correction in the case of a non-uniform drop concentration. The correction depends on
${\it\delta}$. The model also predicts a correction in the case of a non-uniform drop concentration. The correction depends on 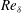 $Re_{{\it\delta}}$, the film Schmidt number, the drop aspect ratio and the diffusivity ratio between the two phases. This prediction is in remarkable agreement with experimental data at low drop Péclet number. It continues to agree as
$Re_{{\it\delta}}$, the film Schmidt number, the drop aspect ratio and the diffusivity ratio between the two phases. This prediction is in remarkable agreement with experimental data at low drop Péclet number. It continues to agree as 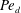 $\mathit{Pe}_{d}$ approaches
$\mathit{Pe}_{d}$ approaches 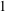 $1$, although the influence of the Reynolds number increases such that
$1$, although the influence of the Reynolds number increases such that 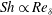 $\mathit{Sh}\propto \mathit{Re}_{{\it\delta}}$.
$\mathit{Sh}\propto \mathit{Re}_{{\it\delta}}$.