Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T02:38:30.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible mixing layer in shock-induced separation

Published online by Cambridge University Press:  28 January 2019

P. Dupont Open the ORCID record for P. Dupont [Opens in a new window] ,
S. Piponniau Open the ORCID record for S. Piponniau [Opens in a new window]  and
J. P. Dussauge
P. Dupont
Affiliation:
Aix Marseille University, CNRS, IUSTI, Marseille, France
S. Piponniau*
Affiliation:
Aix Marseille University, CNRS, IUSTI, Marseille, France
J. P. Dussauge
Affiliation:
Aix Marseille University, CNRS, IUSTI, Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Unsteadiness in separated shock–boundary layer interactions have been previously analysed in order to propose a scenario of entrainment–discharge as the origin of unsteadiness. It was assumed that the fluid in the separated zone is entrained by the free shear layer formed at its edge, and that this layer follows the properties of the canonical mixing layer. 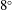This last point is addressed by reanalysing the velocity measurements in an oblique shock reflection at a nominal Mach number of 2.3 and for two cases of flow deviation ($8^{\circ }$ and 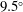$9.5^{\circ }$). The rate of spatial growth of this layer is evaluated from the spatial growth of the turbulent stress profiles. Moreover, the entrainment velocity at the edge of the layer is determined from the mean velocity profiles. It is shown that the values of turbulent shear stress, spreading rate and entrainment velocity are consistent, and that they follow the classical laws for turbulent transport in compressible shear layers. Moreover, the measurements suggest that the vertical normal stress is sensitive to compressibility, so that the anisotropy of turbulence is affected by high Mach numbers. Dimensional considerations proposed by Brown & Roshko (J. Fluid Mech., vol. 64, 1974, 775–781) are reformulated to explain this observed trend.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Compressible boundary layers Turbulent Flows: Shear layer turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 620 - 643
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agostini, L., Larchevêque, L., Dupont, P., Debiève, J. F. & Dussauge, J. P. 2012 Zones of influence and shock motion in a shock boundary layer interaction. AIAA J. 50 (6), 1377–1387.10.2514/1.J051516Google Scholar
Babinsky, H. & Harvey, J. K. 2011 Shock Wave Boundary Layer Interactions. Cambridge University Press.10.1017/CBO9780511842757Google Scholar
Babinsky, H., Oorebeek, J. & Cottingham, T. 2013 Corner effects in reflecting oblique shock-wave/boundary-layer interactions. In Aerospace Sciences Meetings. American Institute of Aeronautics and Astronautics.Google Scholar
Barre, S., Quine, C. & Dussauge, J. P. 1994 Compressibility effects on the structure of supersonic mixing layers: experimental results. J. Fluid Mech. 259, 47–78.10.1017/S0022112094000030Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.10.2514/3.10519Google Scholar
Birch, S. F. & Eggers, J. M.1973 A critical review of the experimental data for developed free turbulent shear layers. Tech. Rep. Nasa Langley Research Center.Google Scholar
Bradshaw, P. 1966 The effect of initial conditions on the development of a free shear layer. J. Fluid Mech. 26 (2), 225–236.10.1017/S0022112066001204Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structures in turbulent mixing layers. J. Fluid Mech. 64, 775–781.10.1017/S002211207400190XGoogle Scholar
Champagne, F. H., Pao, Y. H. & Wygnanski, I. J. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74, 209–250.10.1017/S0022112076001778Google Scholar
Chandrsuda, C. & Bradshaw, P. 1981 Turbulence structure of a reattaching mixing layer. J. Fluid Mech. 110, 171–194.10.1017/S0022112081000670Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46 (1), 469–492.10.1146/annurev-fluid-010313-141346Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Debisschop, J. R., Chambres, O. & Bonnet, J. P. 1994 Velocity field characteristics in supersonic mixing layers. Exp. Therm. Fluid Sci. 9, 147–155.10.1016/0894-1777(94)90107-4Google Scholar
Délery, J. M. & Marvin, J. G.1986 Shock wave-boundary layer interactions. Tech. Rep.Google Scholar
Doerffer, P., Hirsch, C., Dussauge, J.-P., Babinsky, H. & Barakos, G. N.(Eds) 2009 Unsteady Effects of Shock Wave induced Separation, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 114. Springer.Google Scholar
Dupont, P., Haddad, C., Ardissone, J. P. & Debiève, J. F. 2005 Space and time organisation of a shock wave/turbulent boundary layer interaction. Aerosp. Sci. Technol. 9 (7), 561–572.10.1016/j.ast.2004.12.009Google Scholar
Dupont, P., Haddad, C. & Debiève, J. F. 2006 Space and time organization in a shock induced boundary layer. J. Fluid Mech. 559, 255–277.10.1017/S0022112006000267Google Scholar
Dupont, P., Piponniau, S., Sidorenko, A. & Debiève, J. F. 2008 Investigation of an oblique shock reflection with separation by PIV measurements. AIAA J. 46 (6), 1365–1370.10.2514/1.30154Google Scholar
Dussauge, J. P. & Dupont, P. 2005 On critical aerodynamic phenomena in compressible turbulent flows and their measurement: an issue for pivand optical methods. In Proceedings of PIVNet II International Workshop on Application of PIV in Compressible Flows. TU Delft, NL.Google Scholar
Dussauge, J. P., Dupont, P. & Debiève, J. F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10, 85–91.10.1016/j.ast.2005.09.006Google Scholar
Dussauge, J.-P., Dupont, P., Sandham, N. & Garnier, E.2013 Planar shock-wave boundary-layer interaction. Tech. Rep.. UFR 3-32, ERCOFTAC-CFD Qnetknowledge data base.Google Scholar
Dussauge, J. P. & Piponniau, S. 2008 Shock/boundary-layer interactions: Possible sources of unsteadiness. J. Fluids Struct. 24 (8), 1166–1175.10.1016/j.jfluidstructs.2008.06.003Google Scholar
Eagle, W. E. & Driscoll, J. F. 2014 Shock wave-boundary layer interactions in rectangular inlets: three-dimensional separation topology and critical points. J. Fluid Mech. 756, 328–353.10.1017/jfm.2014.382Google Scholar
Elena, M., Tedeschi, G. & Gouin, H. 1999 Motion of tracer particles in supersonic flows. Exp. Fluids 26 (4), 288–296.Google Scholar
Elliott, G. S. & Samimy, M. 1990 Compressibility effects in free shear layers. Phys. Fluids A 2, 1231–1240.10.1063/1.857816Google Scholar
Forliti, D. J., Tang, B. A. & Strykowski, P. J. 2005 An experimental investigation of planar countercurrent turbulent shear layers. J. Fluid Mech. 530, 241–264.10.1017/S0022112005003642Google Scholar
Garnier, E. 2009 Stimulated detached eddy simulation of three–dimensional shock/boundary layer interaction. Shock Waves 19 (6), 479–486.10.1007/s00193-009-0233-7Google Scholar
Goebel, S. G. & Dutton, J. C. 1991 Experimental study of compressible turbulent mixing layers. AIAA J. 29, 538–546.10.2514/3.10617Google Scholar
Helm, C. M., Martin, M. P. & Dupont, P. 2014 Characterization of the Shear Layer in a Mach 3 Shock/Turbulent Boundary Layer Interaction. American Institute of Aeronautics and Astronautics.10.2514/6.2014-0941Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & Van Oudheusden, B. W. 2009a Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.10.1017/S0022112008005090Google Scholar
Humble, R. A., Scarano, F. & Van Oudheusden, B. W. 2009b Unsteady effects in an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.10.1017/S0022112009007630Google Scholar
Jovic, S.1996 An experimental study of a separated/reattached flow behind a backward-facing step. Tech. Rep. NASA Tech. Mem. 110384.Google Scholar
Kiya, M. & Sasaki, K. 1985 Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble. J. Fluid Mech. 154, 463–491.10.1017/S0022112085001628Google Scholar
Klebanoff, P. S.1954 Characteristics of turbulence in a boundary layer with zero pressure gradient. NASA Tech. Rep..Google Scholar
Kline, S. J., Cantwell, B. J. & Lilley, G. M. 1980 Conference on Complex Turbulent Flows, vol. I, pp. 364–366. Stanford University.Google Scholar
Larchevêque, L., Dupont, P., De Martel, E., Garnier, E. & Debiève, J. F. 2009 Experimental and numerical study of unsteadiness in boundary layer/shock wave interaction. 2nd International Conference on Turbulence and Interaction – TI2009, Sainte-Luce, Martinique, France.Google Scholar
Liepmann, H. W. & Laufer, J.1947 Investigation of fre turbulent mixing. Tech. Rep. NACA TN 1257.Google Scholar
Mehta, R. D. & Westphal, R. V. 1986 Near field properties of single- and two-stream plane mixing layers. Exp. Fluids 4, 257–266.10.1007/BF00369117Google Scholar
Menaa, M.1997 Etude expérimentale d’une couche de mélange turbulente supersonique et analyse des propriétés de similitude. PhD thesis, Université de Provence, Marseille.Google Scholar
Na, Y. & Moin, P. 1998 The structure of wall-pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation. J. Fluid Mech. 377, 347–373.10.1017/S0022112098003218Google Scholar
Olsen, M. G. & Dutton, J. C. 2002 Stochastic estimation of large structures in an incompressible mixing layer. AIAA J. 40 (12), 2431–2438.10.2514/2.1611Google Scholar
Olsen, M. G. & Dutton, J. C. 2003 Planar velocity measurements in a weakly compressible mixing layer. J. Fluid Mech. 486, 51–77.10.1017/S0022112003004403Google Scholar
Oster, D. & Wygnanski, I. 1982 The forced mixing layer between parallel streams. J. Fluid Mech. 123, 91–130.10.1017/S0022112082002973Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 29–371.10.1017/S0022112001006978Google Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.10.1017/S0022112088003325Google Scholar
Patel, R. P. 1973 An experimental study of a plane mixing layer. AIAA J. 11, 67–71.Google Scholar
Piponniau, S., Dussauge, J. P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.10.1017/S0022112009006417Google Scholar
Plesniak, M. W., Mehta, R. D. & Johnston, J. P. 1994 Curved two-stream turbulent mixing layers: three-dimensional structure and streamwise evolution. J. Fluid Mech. 270, 1–50.10.1017/S0022112094004180Google Scholar
Plotkin, K. J. 1975 Shock wave oscillation driven by turbulent boundary layer fluctuations. AIAA J. 13 (8), 1036–1040.10.2514/3.60501Google Scholar
Samimy, M. & Elliott, G. S. 1990 Effects of compressibility on the characteristics of free shear layers. AIAA J. 28, 439–445.10.2514/3.10412Google Scholar
Samimy, M. & Lele, S. K. 1991 Motion of particles with inertia in a compressible free shear layer. Phys. Fluids A 3 (8), 1915–1923.10.1063/1.857921Google Scholar
Scharnowski, S., Grayson, K., de Silva, C. M., Hutchins, N., Marusic, I. & Kähler, C. J. 2017 Generalization of the PIV loss-of-correlation formula introduced by Keane and Adrian. Exp. Fluids 58 (10), 150.10.1007/s00348-017-2431-xGoogle Scholar
Slessor, M. D., Zhuang, M. & Dimotakis, P. E. 2000 Turbulent shear-layer mixing: growth-rate compressibility scaling. J. Fluid Mech. 414, 35–45.10.1017/S0022112099006977Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow, 2nd edn. AIP Press.Google Scholar
Spencer, B. W. & Jones, B. G.1971 Statistical investigation of pressure and velocity fields in the turbulent two-stream mixing layer. AIAA Paper 71-813.Google Scholar
Strykowski, P. J., Krothapalli, A. & Jendoubi, S. 1996 The effect of counterflow on the development of compressible shear layers. J. Fluid Mech. 308, 63–96.10.1017/S0022112096001395Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.10.1017/S0022112010005811Google Scholar
Urban, W. D. & Mungal, M. G. 2001 Planar velocity measurements in compressible mixing layers. J. Fluid Mech. 431, 189–222.10.1017/S0022112000003177Google Scholar
Wang, B., Sandham, N. D., Hu, Z. & Liu, W. 2015 Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 767, 526–561.10.1017/jfm.2015.58Google Scholar
Wood, D. H. & Bradshaw, P. 1984 A turbulent mixing layer constrained by a solid surface. Part 2. Measurements in the wall-bounded flow. J. Fluid Mech. 139, 347–361.10.1017/S0022112084000392Google Scholar
Wygnanski, I. & Fiedler, H. E. 1970 The two-dimensional mixing region. J. Fluid Mech. 41, 327–361.10.1017/S0022112070000630Google Scholar