Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T16:04:48.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of premixed flame kernel/turbulence interactions under engine conditions based on direct numerical simulation data

Published online by Cambridge University Press:  27 December 2019

T. Falkenstein Open the ORCID record for T. Falkenstein [Opens in a new window] ,
S. Kang Open the ORCID record for S. Kang [Opens in a new window]  and
H. Pitsch
T. Falkenstein
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, 52056Aachen, Germany
S. Kang
Affiliation:
Department of Mechanical Engineering, Sogang University, Seoul121-742, Republic of Korea
H. Pitsch*
Affiliation:
Institute for Combustion Technology, RWTH Aachen University, 52056Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

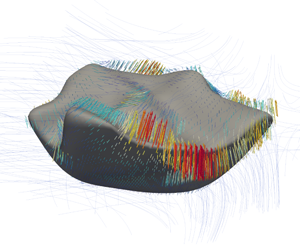
Although the evolution of premixed flames in turbulence has been frequently studied, it is not well understood how small flames interact with large-scale turbulent flow motion. Since this question is of practical importance for the occurrence of cycle-to-cycle variations in spark ignition engines, the objective of the present work is to fundamentally differentiate early flame kernel development from well-established turbulent flame configurations. For this purpose, a direct numerical simulation database consisting of three flames propagating in homogeneous isotropic turbulence (Falkenstein et al., Combust. Flame, 2019, Preprint, arXiv:1908.07556 (accepted)) is considered. The flames feature different ratios of the initially laminar flame diameter to the integral length scale. To quantify flame kernel development, the time evolution of flame topology and flame front geometry are analysed in detail. It is shown that some realizations of the early flame kernel are substantially influenced by high compressive strain caused by large-scale turbulent flow motion with characteristic length scales greater than the flame kernel size. As a result, the initial spherical kernel topology may become highly distorted, which is reflected in the stochastic occurrence of excessive curvature variance. Two mechanisms of curvature production resulting from early flame kernel/turbulence interactions are identified by analysis of the mean curvature balance equation. Further, it is shown that the curvature distribution of small flame kernels becomes strongly skewed towards positive curvatures, which is contrary to developed turbulent flames. Hence, the transition of ignition kernels to self-sustaining turbulent flames is very different in nature compared with the development of a statistically planar flame brush.

JFM classification

Reacting Flows: Combustion Reacting Flows: Flames Reacting Flows: Turbulent reacting flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A32
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-Gayed, R. G., Al-Khishali, K. J. & Bradley, D. 1984 Turbulent burning velocities and flame straining in explosions. Proc. R. Soc. Lond. A 391 (1801), 393–414.CrossRefGoogle Scholar
Akindele, O., Bradley, D., Mak, P. & McMahon, M. 1982 Spark ignition of turbulent gases. Combust. Flame 47, 129–155.CrossRefGoogle Scholar
Aleiferis, P., Taylor, A., Ishii, K. & Urata, Y. 2004 The nature of early flame development in a lean-burn stratified-charge spark-ignition engine. Combust. Flame 136 (3), 283–302.CrossRefGoogle Scholar
Alqallaf, A., Klein, M. & Chakraborty, N. 2019 Effects of Lewis number on the evolution of curvature in spherically expanding turbulent premixed flames. Fluids 4 (1), 12.CrossRefGoogle Scholar
Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.CrossRefGoogle Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5 (1), 113–133.CrossRefGoogle Scholar
Bode, J., Schorr, J., Krüger, C., Dreizler, A. & Böhm, B. 2017 Influence of three-dimensional in-cylinder flows on cycle-to-cycle variations in a fired stratified DISI engine measured by time-resolved dual-plane PIV. Proc. Combust. Inst. 36 (3), 3477–3485.CrossRefGoogle Scholar
Boger, M., Veynante, D., Boughanem, H. & Trouvé, A. 1998 Direct numerical simulation analysis of flame surface density concept for large eddy simulation of turbulent premixed combustion. Symp. (Intl) Combust. 27 (1), 917–925.CrossRefGoogle Scholar
Bradley, D., Lawes, M., Scott, M. & Mushi, E. 1994 Afterburning in spherical premixed turbulent explosions. Combust. Flame 99 (3), 581–590.CrossRefGoogle Scholar
Bradley, D. & Lung, F.-K. 1987 Spark ignition and the early stages of turbulent flame propagation. Combust. Flame 69 (1), 71–93.CrossRefGoogle Scholar
Buschbeck, M., Bittner, N., Halfmann, T. & Arndt, S. 2012 Dependence of combustion dynamics in a gasoline engine upon the in-cylinder flow field, determined by high-speed PIV. Exp. Fluids 53 (6), 1701–1712.CrossRefGoogle Scholar
Buxton, O. R. H., Laizet, S. & Ganapathisubramani, B. 2011 The interaction between strain-rate and rotation in shear flow turbulence from inertial range to dissipative length scales. Phys. Fluids 23 (6), 061704.CrossRefGoogle Scholar
Candel, S. M. & Poinsot, T. J. 1990 Flame stretch and the balance equation for the flame area. Combust. Sci. Technol. 70 (1–3), 1–15.CrossRefGoogle Scholar
Castela, M., Fiorina, B., Coussement, A., Gicquel, O., Darabiha, N. & Laux, C. O. 2016 Modelling the impact of non-equilibrium discharges on reactive mixtures for simulations of plasma-assisted ignition in turbulent flows. Combust. Flame 166, 133–147.CrossRefGoogle Scholar
Chakraborty, N. & Swaminathan, N. 2007 Influence of the Damköhler number on turbulence-scalar interaction in premixed flames. I. Physical insight. Phys. Fluids 19 (4), 045103.Google Scholar
Cifuentes, L., Dopazo, C., Sandeep, A., Chakraborty, N. & Kempf, A. 2018 Analysis of flame curvature evolution in a turbulent premixed bluff body burner. Phys. Fluids 30 (9), 095101.CrossRefGoogle Scholar
Colin, O. & Truffin, K. 2011 A spark ignition model for large eddy simulation based on an FSD transport equation (ISSIM-LES). Proc. Combust. Inst. 33 (2), 3097–3104.CrossRefGoogle Scholar
Creta, F., Lamioni, R., Lapenna, P. E. & Troiani, G. 2016 Interplay of Darrieus–Landau instability and weak turbulence in premixed flame propagation. Phys. Rev. E 94, 053102.Google ScholarPubMed
Damköhler, G. 1940 Der Einfluss der Turbulenz auf die Flammengeschwindigkeit in Gasgemischen. Z. Elektrochem. 46 (11), 601–626.Google Scholar
Dopazo, C., Martin, J., Cifuentes, L. & Hierro, J. 2018 Strain, rotation and curvature of non-material propagating iso-scalar surfaces in homogeneous turbulence. Flow Turbul. Combust. 101 (1), 1–32.CrossRefGoogle Scholar
Echekki, T. & Chen, J. 1999 Analysis of the contribution of curvature to premixed flame propagation. Combust. Flame 118, 308–311.CrossRefGoogle Scholar
Echekki, T. & Kolera-Gokula, H. 2007 A regime diagram for premixed flame kernel-vortex interactions. Phys. Fluids 19 (4), 043604.CrossRefGoogle Scholar
Echekki, T., Poinsot, T., Baritaud, T. & Trouvé, A.1994 Modeling and simulation of turbulent flame kernel evolution. Tech. Rep. 41525. Institut Français du Pétrole.Google Scholar
Falkenstein, T., Kang, S., Cai, L., Bode, M. & Pitsch, H.2019 DNS study of the global heat release rate during early flame kernel development under engine conditions. Combust. Flame, Preprint, arXiv:1908.07556 (accepted).Google Scholar
Fansler, T. D. & Wagner, R. M. 2015 Cyclic dispersion in engine combustion – introduction by the special issue editors. Intl J. Engine Res. 16 (3), 255–259.Google Scholar
Gashi, S., Hult, J., Jenkins, K. W., Chakraborty, N., Cant, S. & Kaminski, C. F. 2005 Curvature and wrinkling of premixed flame kernels comparisons of oh plif and DNS data. Proc. Combust. Inst. 30 (1), 809–817.CrossRefGoogle Scholar
Haq, M., Sheppard, C., Woolley, R., Greenhalgh, D. & Lockett, R. 2002 Wrinkling and curvature of laminar and turbulent premixed flames. Combust. Flame 131 (1), 1–15.CrossRefGoogle Scholar
Hasse, C. 2016 Scale-resolving simulations in engine combustion process design based on a systematic approach for model development. Intl J. Engine Res. 17 (1), 44–62.CrossRefGoogle Scholar
Heim, D. & Ghandhi, J. 2011 A detailed study of in-cylinder flow and turbulence using PIV. SAE Intl J. Engines 4 (1), 1642–1668.CrossRefGoogle Scholar
Herweg, R. & Maly, R. R. 1992 A fundamental model for flame kernel formation in SI engines. In International Fuels Lubricants Meeting Exposition. SAE International.Google Scholar
Hesse, H., Chakraborty, N. & Mastorakos, E. 2009 The effects of the Lewis number of the fuel on the displacement speed of edge flames in igniting turbulent mixing layers. Proc. Combust. Inst. 32 (1), 1399–1407.CrossRefGoogle Scholar
Heywood, J. 1994 Combustion and its modeling in spark-ignition engines. In Proceedings of the Third International Symposium on Diagnostics and Modeling of Combustion in Internal Combustion Engines (COMODIA), Yokohama, Japan, July 11–14, pp. 1–15.Google Scholar
Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1954 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
Jung, D., Sasaki, K. & Iida, N. 2017 Effects of increased spark discharge energy and enhanced in-cylinder turbulence level on lean limits and cycle-to-cycle variations of combustion for SI engine operation. Appl. Energy 205, 1467–1477.CrossRefGoogle Scholar
Karlovitz, B., Denniston, D. W. & Wells, F. E. 1951 Investigation of turbulent flames. J. Chem. Phys. 19 (5), 541–547.CrossRefGoogle Scholar
Kim, S. H. & Pitsch, H. 2007 Scalar gradient and small-scale structure in turbulent premixed combustion. Phys. Fluids 19 (11), 115104.CrossRefGoogle Scholar
Luca, S., Attili, A., Schiavo, E. L., Creta, F. & Bisetti, F. 2019 On the statistics of flame stretch in turbulent premixed jet flames in the thin reaction zone regime at varying Reynolds number. Proc. Combust. Inst. 37 (2), 2451–2459.CrossRefGoogle Scholar
Meneveau, C. & Poinsot, T. 1991 Stretching and quenching of flamelets in premixed turbulent combustion. Combust. Flame 86 (4), 311–332.CrossRefGoogle Scholar
Müller, B. 1998 Low-Mach-number asymptotics of the Navier–Stokes equations. J. Engng Maths 34 (1), 97–109.CrossRefGoogle Scholar
Peters, N. 1992 A spectral closure for premixed turbulent combustion in the flamelet regime. J. Fluid Mech. 242, 611–629.CrossRefGoogle Scholar
Peters, N. 1999 The turbulent burning velocity for large-scale and small-scale turbulence. J. Fluid Mech. 384, 107–132.CrossRefGoogle Scholar
Peterson, B., Reuss, D. L. & Sick, V. 2011 High-speed imaging analysis of misfires in a spray-guided direct injection engine. Proc. Combust. Inst. 33 (2), 3089–3096.CrossRefGoogle Scholar
Peterson, B., Reuss, D. L. & Sick, V. 2014 On the ignition and flame development in a spray-guided direct-injection spark-ignition engine. Combust. Flame 161 (1), 240–255.CrossRefGoogle Scholar
Pitsch, H. & Peters, N. 1996 Numerical and asymptotic studies of the structure of premixed iso-octane flames. Symp. (Intl) Combust. 26 (1), 763–771.CrossRefGoogle Scholar
Poludnenko, A. & Oran, E. 2011 The interaction of high-speed turbulence with flames: turbulent flame speed. Combust. Flame 158 (2), 301–326.CrossRefGoogle Scholar
Pope, S. B. 1988 The evolution of surfaces in turbulence. Intl J. Engng Sci. 26, 445–469.CrossRefGoogle Scholar
Reddy, H. & Abraham, J. 2013 Influence of turbulence-kernel interactions on flame development in lean methane/air mixtures under natural gas-fueled engine conditions. Fuel 103, 1090–1105.CrossRefGoogle Scholar
Richard, S., Colin, O., Vermorel, O., Benkenida, A., Angelberger, C. & Veynante, D. 2007 Towards large eddy simulation of combustion in spark ignition engines. Proc. Combust. Inst. 31 (2), 3059–3066.CrossRefGoogle Scholar
Rutland, C. J. 2011 Large-eddy simulations for internal combustion engines – a review. Intl J. Engine Res. 12 (5), 421–451.CrossRefGoogle Scholar
Schiffmann, P., Reuss, D. L. & Sick, V. 2018 Empirical investigation of spark-ignited flame-initiation cycle-to-cycle variability in a homogeneous charge reciprocating engine. Intl J. Engine Res. 19 (5), 491–508.CrossRefGoogle Scholar
Scurlock, A. & Grover, J. 1953 Propagation of turbulent flames. Symp. (Intl) Combust. 4 (1), 645–658.CrossRefGoogle Scholar
Shepherd, I. & Ashurst, W. 1992 Flame front geometry in premixed turbulent flames. Symp. (Intl) Combust. 24 (1), 485–491.CrossRefGoogle Scholar
Shepherd, I., Cheng, R., Plessing, T., Kortschik, C. & Peters, N. 2002 Premixed flame front structure in intense turbulence. Proc. Combust. Inst. 29 (2), 1833–1840.CrossRefGoogle Scholar
Subramanian, V., Domingo, P. & Vervisch, L. 2009 Turbulent flame spreading mechanisms after spark ignition. AIP Conf. Proc. 1190 (1), 68–89.CrossRefGoogle Scholar
Thévenin, D. 2005 Three-dimensional direct simulations and structure of expanding turbulent methane flames. Proc. Combust. Inst. 30 (1), 629–637.CrossRefGoogle Scholar
Thévenin, D., Gicquel, O., Charentenay, J. D., Hilbert, R. & Veynante, D. 2002 Two- versus three-dimensional direct simulations of turbulent methane flame kernels using realistic chemistry. Proc. Combust. Inst. 29 (2), 2031–2039.CrossRefGoogle Scholar
Uranakara, H. A., Chaudhuri, S. & Lakshmisha, K. 2017 On the extinction of igniting kernels in near-isotropic turbulence. Proc. Combust. Inst. 36 (2), 1793–1800.CrossRefGoogle Scholar
Vasudeo, N., Echekki, T., Day, M. S. & Bell, J. B. 2010 The regime diagram for premixed flame kernel-vortex interactions – revisited. Phys. Fluids 22 (4), 043602.CrossRefGoogle Scholar
Wang, H., Hawkes, E. R., Chen, J. H., Zhou, B., Li, Z. & Aldén, M. 2017a Direct numerical simulations of a high Karlovitz number laboratory premixed jet flame – an analysis of flame stretch and flame thickening. J. Fluid Mech. 815, 511–536.CrossRefGoogle Scholar
Wang, Z., Liu, H. & Reitz, R. D. 2017b Knocking combustion in spark-ignition engines. Progr. Energy Combust. Sci. 61, 78–112.CrossRefGoogle Scholar
Wenzel, H. & Peters, N. 2000 Direct numerical simulation and modeling of kinematic restoration, dissipation and gas expansion effects of premixed flames in homogeneous turbulence. Combust. Sci. Technol. 158 (1), 273–297.CrossRefGoogle Scholar
Young, M. B. 1981 Cyclic dispersion in the homogeneous-charge spark-ignition engine – a literature survey. SAE Trans. 90, 49–73.Google Scholar
Zel’dovich, Y. B. 1966 An effect which stabilizes the curved front of a laminar flame. J. Appl. Mech. Techn. Phys. 7 (1), 68–69.CrossRefGoogle Scholar
Zeng, W., Keum, S., Kuo, T.-W. & Sick, V. 2019 Role of large scale flow features on cycle-to-cycle variations of spark-ignited flame-initiation and its transition to turbulent combustion. Proc. Combust. Inst. 37 (4), 4945–4953.CrossRefGoogle Scholar
Supplementary material: File

Falkenstein et al. supplementary material

Falkenstein et al. supplementary material

Download Falkenstein et al. supplementary material(File)
File 12.5 MB