Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T22:56:09.634Z Has data issue: false hasContentIssue false
  • English
  • Français

A threshold AR(1) model

Published online by Cambridge University Press:  14 July 2016

Joseph D. Petruccelli  and
Samuel W. Woolford
Joseph D. Petruccelli*
Affiliation:
Worcester Polytechnic Institute
Samuel W. Woolford*
Affiliation:
Worcester Polytechnic Institute
*
∗ Postal address: Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA 01609, U.S.A.
∗ Postal address: Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA 01609, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

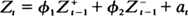We consider the model where φ1, φ2 are real coefficients, not necessarily equal, and the at,'s are a sequence of i.i.d. random variables with mean 0. Necessary and sufficient conditions on the φ 's are given for stationarity of the process. Least squares estimators of the φ 's are derived and, under mild regularity conditions, are shown to be consistent and asymptotically normal. An hypothesis test is given to differentiate between an AR(1) (the case φ1 = φ2) and this threshold model. The asymptotic behavior of the test statistic is derived. Small-sample behavior of the estimators and the hypothesis test are studied via simulated data.

Keywords

NON-LINEAR TIME SERIESTAR MODELSAUTOREGRESSIVE MODELSMARKOV CHAINS
Type
Research Papers
Information
Journal of Applied Probability , Volume 21 , Issue 2 , June 1984 , pp. 270 - 286
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2. Wiley, New York.Google Scholar
Hannan, E. J. (1970) Multiple Time Series. Wiley, New York.CrossRefGoogle Scholar
Jones, D. A. (1978) Nonlinear autoregressive processes. Proc. R. Soc. London A 360, 71–95.Google Scholar
Klimko, L. A. and Nelson, P. I. (1978) On conditional least squares estimation for stochastic processes. Ann. Statist. 6, 629–642.CrossRefGoogle Scholar
Orey, S. (1971) Limit Theorems for Markov Chain Transition Probabilities. Van Nostrand Reinhold, New York.Google Scholar
Priestley, M. B. (1980) State-dependent models: a general approach to non-linear time series analysis. J. Time Series Analysis 1, 47–71.Google Scholar
Tong, H. (1978) On a threshold model. In Pattern Recognition and Signal Processing, ed. Chen, C. H., Sijthoof and Nordhoff, Alphen aan den Rijn, The Netherlands.Google Scholar
Tong, H. and Lim, K. S. (1980) Threshold autoregression, limit cycles and cyclical data. J. R. Statist. Soc. B42, 245–292.Google Scholar
Tweedie, R. L. (1974) R-theory for Markov chains on a general state space I: solidarity properties and R-recurrent chains. Ann. Prob. 2, 840–864.Google Scholar
Tweedie, R. L. (1975) Sufficient conditions for ergodicity and recurrence of Markov chains on a general state space. Stoch. Proc. Appl. 3, 385–403.CrossRefGoogle Scholar
Wecker, W. E. (1977) Asymmetric time series. ASA Proc. Business and Economic Section, 417–422.Google Scholar