Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Georgii, Hans-Otto
Häggström, Olle
and
Maes, Christian
2001.
Vol. 18,
Issue. ,
p.
1.
Cannings, C.
and
Penman, D.B.
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
51.
Hunter, David R.
Krivitsky, Pavel N.
and
Schweinberger, Michael
2012.
Computational Statistical Methods for Social Network Models.
Journal of Computational and Graphical Statistics,
Vol. 21,
Issue. 4,
p.
856.
Yin, Mei
2012.
A cluster expansion approach to exponential random graph models.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2012,
Issue. 05,
p.
P05004.
Robins, Garry
2012.
Computational Complexity.
p.
2953.
Chatterjee, Sourav
and
Diaconis, Persi
2013.
Estimating and understanding exponential random graph models.
The Annals of Statistics,
Vol. 41,
Issue. 5,
Yin, Mei
2013.
Critical Phenomena in Exponential Random Graphs.
Journal of Statistical Physics,
Vol. 153,
Issue. 6,
p.
1008.
Radin, Charles
and
Yin, Mei
2013.
Phase transitions in exponential random graphs.
The Annals of Applied Probability,
Vol. 23,
Issue. 6,
Koskinen, Johan
and
Lomi, Alessandro
2013.
The Local Structure of Globalization.
Journal of Statistical Physics,
Vol. 151,
Issue. 3-4,
p.
523.
Aristoff, David
and
Zhu, Lingjiong
2015.
Asymptotic structure and singularities in constrained directed graphs.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 11,
p.
4154.
Lubetzky, Eyal
and
Zhao, Yufei
2015.
On replica symmetry of large deviations in random graphs.
Random Structures & Algorithms,
Vol. 47,
Issue. 1,
p.
109.
Yin, Mei
2016.
A Detailed Investigation into Near Degenerate Exponential Random Graphs.
Journal of Statistical Physics,
Vol. 164,
Issue. 1,
p.
241.
Kenyon, Richard
and
Yin, Mei
2017.
On the asymptotics of constrained exponential random graphs.
Journal of Applied Probability,
Vol. 54,
Issue. 1,
p.
165.
Wilson, James D.
Denny, Matthew J.
Bhamidi, Shankar
Cranmer, Skyler J.
and
Desmarais, Bruce A.
2017.
Stochastic weighted graphs: Flexible model specification and simulation.
Social Networks,
Vol. 49,
Issue. ,
p.
37.
Aristoff, David
and
Zhu, Lingjiong
2018.
On the phase transition curve in a directed exponential random graph model.
Advances in Applied Probability,
Vol. 50,
Issue. 01,
p.
272.
Koskinen, Johan
2018.
Wiley StatsRef: Statistics Reference Online.
p.
1.
Schweinberger, Michael
2019.
Wiley StatsRef: Statistics Reference Online.
p.
1.
Babkin, Sergii
Stewart, Jonathan R.
Long, Xiaochen
and
Schweinberger, Michael
2020.
Large-scale estimation of random graph models with local dependence.
Computational Statistics & Data Analysis,
Vol. 152,
Issue. ,
p.
107029.
Yin, Fan
Butts, Carter T.
and
De Vico Fallani, Fabrizio
2022.
Highly scalable maximum likelihood and conjugate Bayesian inference for ERGMs on graph sets with equivalent vertices.
PLOS ONE,
Vol. 17,
Issue. 8,
p.
e0273039.
Marsman, M.
and
Huth, K.
2023.
Idiographic Ising and Divide and Color Models: Encompassing Networks for Heterogeneous Binary Data.
Multivariate Behavioral Research,
Vol. 58,
Issue. 4,
p.
787.
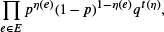 where t(η) is the number of triangles in the open subgraph. In this paper the behavior of the random triangle model on the two-dimensional triangular lattice is studied. By mapping the system onto an Ising model with external field on the hexagonal lattice, it is shown that phase transition occurs if and only if p = (q−1)−2/3 and q > qc for a critical value qc which turns out to equal
where t(η) is the number of triangles in the open subgraph. In this paper the behavior of the random triangle model on the two-dimensional triangular lattice is studied. By mapping the system onto an Ising model with external field on the hexagonal lattice, it is shown that phase transition occurs if and only if p = (q−1)−2/3 and q > qc for a critical value qc which turns out to equal 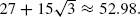 It is furthermore demonstrated that phase transition cannot occur unless p = pc(q), the critical value for percolation of open edges for given q. This implies that for q ≥ qc, pc(q) = (q−1)−2/3.
It is furthermore demonstrated that phase transition cannot occur unless p = pc(q), the critical value for percolation of open edges for given q. This implies that for q ≥ qc, pc(q) = (q−1)−2/3.