Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
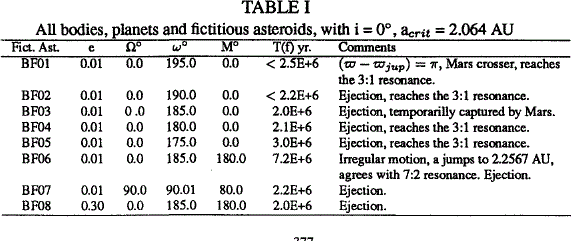
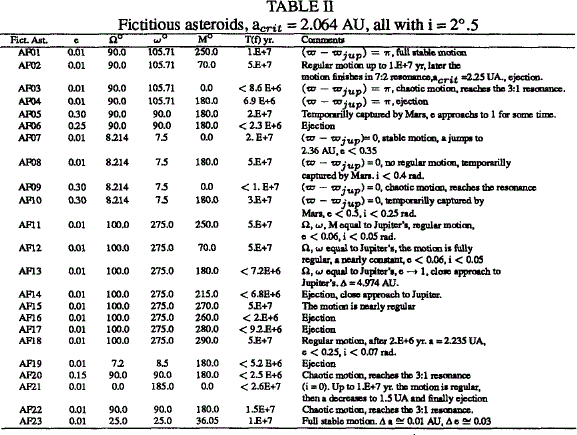
We study the dynamics of mean motion resonance with Jupiter in the 4:1 gap using only gravitational methods. This mechanism is capable of explaining this Kirkwood gap in an uniform way (see Ferraz-Mello, 1994; Ferraz-Mello et al., 1994; Moons, 1997; Yoshikawa, 1989). We considered the asteroidal motion in two and three dimensions and we carried out our investigations integrating numerically the full equations of motion and taking into account Mars, Jupiter and Saturn as disturbing planets. The orbital evolution of asteroids was obtained considering the elements variation. The numerical investigations were carried out using symplectic integrators. These integrations were stopped when the asteroid had close encouters with Mars or Jupiter, this occurs when the distance between the planet and the asteroid is of the order of 0.01 AU or less, or when the eccentricity increases up to 0.9. We studied real and fictitious asteroids on a time scale of 5 × 107 yr. The initial osculating elements of perturbing planets and their inverse masses were taken from the Ephemerides of Minor Planets (EMP) at the epoch of JD 2450000.5. The initial data corresponding to the real asteroids were also taken from the EMP. The starting elements of fictitious asteroids were, in all analyzed cases, a = acrit = 2.064; AU, i = 2°.5 and e = 0.01 (in the majority of cases). The other initial elements are shown in Table II. We have also studied fictitious asteroids with i = 0°, a = acrit and e = 0.01 (Table I). The present analysis leads to the following results: (1) The motions are unstable. The eccentricity, in the majority of cases, has very large increase. It may grow up to 0.9 in 106 yr. The semi major axis has large variations then, owing to both effects some fictitious asteroids reach the 3:1 resonance while others reach 7:2 resonance in a few million years, they are very chaotic regions. (2) The eccentricities of fictitious asteroids become large by the effect of the secular resonance v6, i.e. when (ϖ − ϖSat) ≅ 0, the rate of this resonance is 26.217”/year with period ~ 4.9 × 104 years (Bretagnon, 1974). (3) The fictitious asteroids studied with a = acrit, e < 0.05 and i < 3° are removed of this gap mainly by the effects of the secular resonances v6 and v16 (see Moons and Morbidelli, 1995; Williams, 1969). (4) There are close encounters with Mars or eventually with the Earth (not considered here) in a time scale of 106 - 107 yr. (5) For certain initial conditions some fictitious asteroids are temporally captured by Mars and in some cases for a long time. (6) If a = acrit,e = 0.3 and the inclination is less than 3°, Mars and asteroid’s perihelion are very close ( ~ 0.06AU ). This situation helps the capture. (7) The (a,e)-plane was used to determine the dynamical behaviour of all asteroids and we found that the 4:1 resonance is very strong. The Lyapunov times are very short.
