Discontinuity Modes in Polytropes

Abstract

In the calculation of linear nonradial oscillation modes in composite polytropes with a small density discontinuity, a discontinuity mode may occur. This mode consists of a wave propagating along the discontinuity interface with a large amplitude that declines exponentially away from the interface. The period P of this mode is well-estimated (to within 10%) by

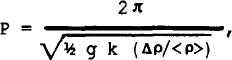
where Δρ/<ρ> is the fractional density discontinuity and k is the horizontal wavenumber (c.f. Gabriel and Scuflaire 1980, in Nonradial and Nonlinear Stellar Pulsation, eds. H. Hill and W. Dziembowski, Springer-Verlag). For a 12 solar-mass polytrope with a radius of 4.27 R_⊙, a 3% density discontinuity at fractional radius 0.15 produces a discontinuity mode with a period of 7.329 hours. As the density discontinuity increases the period P decreases, resulting in avoided crossings with the normal g-mode spectrum. Between these avoided crossings, the discontinuity mode has an unusually large amplitude at the location of the discontinuity.