No CrossRef data available.
Article contents
Can Combination of ‘Kozai Effect’ and Tidal Friction Produce Close Stellar and Planetary Orbits?
Published online by Cambridge University Press: 12 April 2016
Extract
In binary stars, tidal friction dissipates a fraction of the orbital energy at constant angular momentum and will circularise binary orbits on a rather short rimescale compared with the nuclear rimescale, provided that at least one star of the binary has a radius comparable to the separation between binary components. This dissipation effectively ceases once the orbit is circularised. In a hierarchical triple system such dissipation cannot cease entirely, as neither inner nor outer orbit can become exactly circular because of the perturbation of the third distant body. Thus in such systems tidal friction can lead to a steady secular decrease of the inner semimajor axis, accompanied by transfer of angular momentum from the inner to the outer pair, persisting over the whole nuclear lifetime of the system. The situation can be even more dramatic if two orbits have high relative inclination i > 40° It can be shown analytically and numerically (see e.g., Kozai 1962, Marchal 1990, Kiseleva 1996 and references therein) that for triple systems with high relative inclination there is a quasi-periodic change of the inner eccentricity (on a timescale 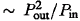 ) during which it reaches a maximum value
) during which it reaches a maximum value 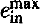 . This value only depends on the inclination i between the two orbital planes; other parameters affect only the timescale. For example, if we approximate a triple stellar system like β Per (Algol) (m1 = 0.8M⊙, m2 = 3.7M⊙, Pin = 2.87 days; m3 = 1.7M⊙, Pout = 1.86 yr, eout = 0.23; i = 100°) as three point masses, then the inner eccentricity ein cycles rather smoothly between 0 and 0.985, while i fluctuates between 100° and 140°. We call these fluctuations ‘Kozai cycles’. Such ‘Kozai cycles’ do not actually occur in this semi-detached system: they can be damped to a small value by tidal friction, but in fact they are also strongly reduced by the non-dissipative effect of the quadrupole moments of the two stars in the inner pair. This effect produces apsidal motion which is much more rapid than the apsidal motion due to the third star, and so prevents the Kozai cycles from operating.
. This value only depends on the inclination i between the two orbital planes; other parameters affect only the timescale. For example, if we approximate a triple stellar system like β Per (Algol) (m1 = 0.8M⊙, m2 = 3.7M⊙, Pin = 2.87 days; m3 = 1.7M⊙, Pout = 1.86 yr, eout = 0.23; i = 100°) as three point masses, then the inner eccentricity ein cycles rather smoothly between 0 and 0.985, while i fluctuates between 100° and 140°. We call these fluctuations ‘Kozai cycles’. Such ‘Kozai cycles’ do not actually occur in this semi-detached system: they can be damped to a small value by tidal friction, but in fact they are also strongly reduced by the non-dissipative effect of the quadrupole moments of the two stars in the inner pair. This effect produces apsidal motion which is much more rapid than the apsidal motion due to the third star, and so prevents the Kozai cycles from operating.
- Type
- Extended Abstracts
- Information
- International Astronomical Union Colloquium , Volume 172: Impact of Modern Dynamics in Astronomy , 1999 , pp. 409 - 410
- Copyright
- Copyright © Kluwer 1999


