Published online by Cambridge University Press: 18 May 2009
Let 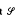 be the semigroup of all total one-to-one transformations of an infinite set X. For an ƒ ∈
be the semigroup of all total one-to-one transformations of an infinite set X. For an ƒ ∈ 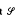 let the defect of ƒ def ƒ, be the cardinality of X – R(ƒ), where R(ƒ) = ƒ(X) is the range of ƒ. Then
let the defect of ƒ def ƒ, be the cardinality of X – R(ƒ), where R(ƒ) = ƒ(X) is the range of ƒ. Then 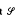 is a disjoint union of the symmetric group
is a disjoint union of the symmetric group 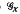 x on X, the semigroup S of all transformations in
x on X, the semigroup S of all transformations in 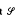 with finite non-zero defects and the semigroup Ā of all transformations in S with infinite defects, such that S U Ā and Ā are ideals of
with finite non-zero defects and the semigroup Ā of all transformations in S with infinite defects, such that S U Ā and Ā are ideals of 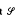 . The properties of
. The properties of 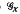 x and Ā have been investigated by a number of authors (for the latter it was done via Baer-Levi semigroups, see [2], [3], [5], [6], [7], [8], [9], [10] and note that Ā decomposes into a union of Baer–Levi semigroups). Our aim here is to study the semigroup S. It is not difficult to see that S is left cancellative (we compose functions ƒ, g in S as ƒg(x) = ƒ(g(x)), for x ∈ X) and idempotent-free. All automorphisms of S are inner [4], that is of the form ƒ → hƒhfh-1 ƒ ∈ S, h ∈
x and Ā have been investigated by a number of authors (for the latter it was done via Baer-Levi semigroups, see [2], [3], [5], [6], [7], [8], [9], [10] and note that Ā decomposes into a union of Baer–Levi semigroups). Our aim here is to study the semigroup S. It is not difficult to see that S is left cancellative (we compose functions ƒ, g in S as ƒg(x) = ƒ(g(x)), for x ∈ X) and idempotent-free. All automorphisms of S are inner [4], that is of the form ƒ → hƒhfh-1 ƒ ∈ S, h ∈ 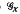 x.
x.