Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T21:35:35.800Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite full transformation semigroups as collections of random functions

Published online by Cambridge University Press:  18 May 2009

B. Brown  and
P. M. Higgins
B. Brown
Affiliation:
Department of Mathematics, University of Tasmania, Sandy Bay, Tasmania 7001, Australia.
P. M. Higgins
Affiliation:
Athematics Section, Deakin University, Victoria, 3217, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The collection of all self-maps on a non-empty set X under composition is known in algebraic semigroup theory as the full transformation semigroup on X and is written 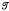x. Its importance lies in the fact that any semigroup S can be embedded in the full transformation semigroup 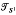(where S1 is the semigroup S with identity 1 adjoined, if S does not already possess one). The proof is similar to Cayley's Theorem that a group G can be embedded in SG, the group of all bijections of G to itself. In this paper X will be a finite set of order n, which we take to be 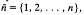and so we shall write Tn for 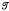X.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 30 , Issue 2 , May 1988 , pp. 203 - 211
Copyright
Copyright © Glasgow Mathematical Journal Trust 1988

References

1.Billingsley, P., Convergences of Probability Measures, (Wiley, 1968).Google Scholar
2.Chung, K. L., A Course in Probability Theory, (Harcourt, Brace and World, 1968).Google Scholar
3.Denes, J., ‘Some Combinatorial Properties of Transformations and their Connections with the Theory of Graphs.’ J. Comb. Thry. 9 (1969) 108–116.CrossRefGoogle Scholar
4.Feller, W., An Introduction to Probability Theory and its Applications, Vol. 1, 3rd ed., (Wiley and Sons, 1968).Google Scholar
5.Harary, F., Graph Theory, (Addison-Wesley, 1969).CrossRefGoogle Scholar
6.Harris, B., The Asymptotic Distribution of the Order of Elements in Symmetric Semigroups, J. Comb. Thry (A) 15 (1973) 66–74.CrossRefGoogle Scholar
7.Higgins, P. M., A method for constructing square roots in finite full transformation semigroups, Canad. Math. Bull. 29 (1986).CrossRefGoogle Scholar
8.Howie, J. M., Idempotent generators in finite full transformation semigroups, Proc. Roy. Soc. Edin. 81A (1978) 317–323.CrossRefGoogle Scholar
9.Kim, K. H. and Roush, F. W., The average rank of a product of transformations, Semigroup Forum 19 (1980), 79–85.CrossRefGoogle Scholar