Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T08:56:50.715Z Has data issue: false hasContentIssue false
  • English
  • Français

CONCERNING SUMMABLE SZLENK INDEX

Part of: Linear spaces and algebras of operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  21 December 2018

RYAN MICHAEL CAUSEY
RYAN MICHAEL CAUSEY*
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the notion of summable Szlenk index from a Banach space to an arbitrary weak*-compact set. We prove that a weak*-compact set has summable Szlenk index if and only if its weak*-closed, absolutely convex hull does. As a consequence, we offer a new, short proof of a result from Draga and Kochanek [J. Funct. Anal. 271 (2016), 642–671] regarding the behavior of summability of the Szlenk index under c0 direct sums. We also use this result to prove that the injective tensor product of two Banach spaces has summable Szlenk index if both spaces do, which answers a question from Draga and Kochanek [Proc. Amer. Math. Soc. 145 (2017), 1685–1698]. As a final consequence of this result, we prove that a separable Banach space has summable Szlenk index if and only if it embeds into a Banach space with an asymptotic c0 finite dimensional decomposition, which generalizes a result from Odell et al. [Q. J. Math. 59, (2008), 85–122]. We also introduce an ideal norm 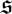$\mathfrak{s}$ on the class 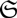$\mathfrak{S}$ of operators with summable Szlenk index and prove that 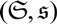$(\mathfrak{S}, \mathfrak{s})$ is a Banach ideal. For 1 ⩽ p ⩽ ∞, we prove precise results regarding the summability of the Szlenk index of an ℓp direct sum of a collection of operators.

MSC classification

Primary: 46B03: Isomorphic theory (including renorming) of Banach spaces 47L20: Operator ideals
Secondary: 46B28: Spaces of operators; tensor products; approximation properties
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 1 , January 2020 , pp. 59 - 73
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argyros, S. A., Gasparis, I. and Motakis, P., On the structure of separable $\mathcal{L}_\infty$-spaces, Mathematika 62(3) (2016), 685–700.CrossRefGoogle Scholar
Baudier, F., Kalton, N. and Lancien, G., A new metric invariant for Banach spaces, Studia Math. 199 (2010), 73–94.CrossRefGoogle Scholar
Causey, R. M., An alternate description of the Szlenk index with applications, Illinois J. Math. 59(2) (2015), 359–390.CrossRefGoogle Scholar
Causey, R. M., Power type ξ-asymptotically uniformly smooth norms, to appear in Trans. Amer. Math. Soc.Google Scholar
Causey, R. M., Power type ξ-asymptotically uniformly smooth and ξ-asymptotically uniformly flat norms, submitted.Google Scholar
Causey, R. M. and Dilworth, S. J., ξ-asymptotically uniformly smooth, ξ-asymptotically uniformly convex, and (β) operators, submitted.Google Scholar
Draga, S. and Kochanek, T., Direct sums and summability of the Szlenk index, J. Funct. Anal. 271 (2016), 642–671.CrossRefGoogle Scholar
Draga, S. and Kochanek, T., The Szlenk power type and injective tensor products of Banach spaces, Proc. Amer. Math. Soc. 145 (2017), 1685–1698.CrossRefGoogle Scholar
Godefroy, G., Kalton, N. and Lancien, G., Subspaces of $c_0(\mathbb{N})$ and Lipschitz isomorphisms, Geom. Funct. Anal. 10 (2000), 798–820.CrossRefGoogle Scholar
Godefroy, G., Kalton, N. and Lancien, G., Szlenk indices and uniform homeomorphisms, Trans. Amer. Math. Soc. 353(1) (2001), 3895–3918.CrossRefGoogle Scholar
Junge, M., Kutzarova, D. and Odell, E., On asymptotically symmetric Banach spaces, Studia Math. 173 (2006), 203–231.CrossRefGoogle Scholar
Kalton, N. and Randrianarivony, L., The coarse Lipschitz structure of ℓ p ⊕ ℓ q, Math. Ann. 341 (2008), 223–237.CrossRefGoogle Scholar
Knaust, H., Schlumprecht, Th. and Odell, E., On Asymptotic structure, the Szlenk index and UKK properties in Banach spaces, Positivity 3 (1999), 173–199.CrossRefGoogle Scholar
Lancien, G. and Raja, M., Asymptotic and coarse Lipschitz structures of quasi-reflexive Banach spaces, Houston J. of Math. 44(3) (2018), 927–940.Google Scholar
Odell, E. and Schlumprecht, Th., Trees and branches in Banach spaces, Trans. Amer. Math. Soc. 354(10) (2002), 4085–4108.CrossRefGoogle Scholar
Odell, E., Schlumprecht, Th. and Zsak, A., On the structure of asymptotic ℓ p spaces, Q. J. Math. 59, (2008), 85–122.Google Scholar
Ryan, R. A., Introduction to tensor products of Banach spaces, Springer Monographs in Mathematics (Springer-Verlag London, Ltd., London, 2002).Google Scholar
Schlumprecht, Th., On Zippin’s embedding theorem, Adv. Math. 274 (2015), 833–880.CrossRefGoogle Scholar
Szlenk, W., The non existence of a separable reflexive Banach space universal for all separable reflexive Banach spaces, Studia Math. 30 (1968), 53–61.CrossRefGoogle Scholar