What do artificial neural networks tell us about the genetic structure of populations? The example of European pig populations

Summary

General and genetic statistical methods are commonly used to deal with microsatellite data (highly variable neutral genetic markers). In this paper, the self-organizing map (SOM) that belongs to the unsupervised artificial neural networks (ANNs) was applied to analyse the structure of 58 European and two Chinese pig populations (Sus scrofa) including commercial lines, local breeds and cosmopolitan breeds. Results were compared with other unsupervised classification or ordination methods such as factorial correspondence analysis, hierarchical clustering from an allele sharing distance and the Bayesian genetic model and with principal components analysis and neighbour joining from allelic frequencies and genetic distances between populations. Like other methods, SOMs were able to classify individuals according to their breed origin and to visualize similarities between breeds. They provided additional information on the within- and between-population diversity, allowed differences between similar populations to be highlighted and helped differentiate different groups of populations.

1. Introduction

The availability of many genetic markers allowed large-scale surveys of genetic diversity to be carried out in various species. Such projects have provided large data sets that give access to a detailed knowledge of the genetic structure of populations. Most analyses have made use of methods based on population genetic models that allow specific evolutionary hypotheses to be addressed. Using more general descriptive tools may, however, provide complementary points of view and suggest new questions. In most biological sciences, parametric and non-parametric multivariate analyses are commonly used as classification methods (e.g. Sparling & Williams, 1978; Martindale, 1980; Figueredo et al., 1992; Le Pape & Chevalet, 1992; Terhune et al., 1993). Nevertheless, some limitations are known: strong distortions with nonlinear data sets (Kenkel & Orloci, 1986), horseshoe effects due to unimodal response curves in principal components analysis (PCA), arch effects, outliers, missing data, etc. (Giraudel & Lek, 2001). Linear multivariate approaches (such as PCA or factorial correspondence analysis) used to analyse large genetic data sets did not allow a large part of the total variance or inertia to be explained by the first main principal components. As an alternative tool to deal with this problem of complexity in biological data, artificial neural networks (ANNs) have been used for patterning samples in biological systems, such as segmentation of brain images (Vijayakumar et al., 2007). ANNs have proved their utility in various fields. They have been widely used in the areas of word recognition (Waibel et al., 1989; Lefebvre et al., 1990; Gemello & Mana, 1991; Maravall et al., 1991), chemistry and physics but less in population genetics and ecology. Previous work using ANNs concerned, for example, classification in the behavioural sciences (Reby et al., 1997; Park et al., 2005), evaluation of the contribution of repopulation to biodiversity (Aurelle et al., 1999; Zhu, 2004), genetic analysis of populations with highly variable markers such as microsatellites (Cornuet et al., 1996; Aurelle et al., 1999), classification of individuals based on genotypic data (Guinand et al., 2002); analysis of the geographic origin of ancient patrilineal populations (Manni et al., 2005); identification of patterns of genetic diversity (Grigull et al., 2001; Zhao et al., 2005); and identification of biomarkers (Kouskoumvekaki et al., 2008).

In this work, we applied the self-organizing map (SOM; Kohonen, 1982, 2001) method to a large pig (Sus scrofa) genetic data set in order to assess the added value of this unsupervised approach, compared with a previous genetic analysis (SanCristobal et al., 2006) and with other approaches. Three unsupervised methods allowing individuals to be clustered were used: factorial correspondence analysis (FCA), hierarchical clustering based on allele sharing (AS) distances between individuals and a Bayesian approach based on a genetic model (Pritchard et al., 2000). Results were then compared with classifications of populations based on allele frequencies (neighbour joining (NJ) from genetic distances and PCA).

2. Materials and methods

(i) Data

The materials used in this study were available from the European Pig Biodiversity project (PigBioDiv; BIO4 CT 98 0188, http://www.projects.roslin.ac.uk/pigbiodiv/). The objectives of this project were to study the genetic diversity, as well as to improve the understanding of the structure and dynamics of the pig populations in Europe. In this project, about 50 individuals were sampled in each of 60 populations representing 23 local breeds, five cosmopolitan breeds (with 12 Landrace, ten Large White, four Piétrain, three Duroc and two Hampshire populations), four synthetic lines, and two populations of Meishan origin (population originating in China). Genotypes at up to 50 microsatellite markers were available with a total of 2737 individuals and 700 alleles (SanCristobal et al., 2006). Markers have been chosen to be polymorphic, to cover the genome (two to three markers per chromosome), to be genetically independent and for their capability to produce good resolution using automatic DNA analysers and multiplexing (Archibald et al., 1995; Groenen et al., 2003). Although most methods allowed for missing data, 54 individuals with valid genotypes at less than five markers were discarded from all analyses, and 161 more individuals had to be discarded for a specific method (AS, as explained below).

(ii) SOM analysis

The SOM is an unsupervised learning algorithm (Kohonen, 2001), which performs a nonlinear projection of multivariate data onto lower dimension. Formally, it consists of two connected layers of neurons: the input layer (the data) and an output layer. In the output layer, the SOM consists of a two-dimensional finite network arranged on a grid with its own topology. Each piece of data as well as each output neuron is a vector of dimension N, the number of items describing individual data. During the learning process, the algorithm computes the Euclidean distances between an input vector and the output neurons. In the output layer, the best matching neuron (BMN), which has a minimum distance with the input vector, is selected as winner. For the BMN and its neighbours in the output layer, weight vectors are updated to minimize the distance from the input vector.

At the end of the process, each input vector is assigned to one of the output neurons on the grid. Further, a hierarchical clustering and U-matrix algorithm allow boundaries to be defined between clusters on the trained SOM map (Ultsch, 1993; Park et al., 2004). A global quality criterion of the result is given by the topographic error, which is the proportion of individuals for which the first (winning) and the second best matching neurons are not adjacent on the SOM.

Details of the method can be found in Giraudel & Lek (2001) or Park et al. (2004).

Data consisted here of one genetic matrix of 2683 individuals from the 60 pig populations with 700 alleles. Each allele is encoded by the number of copies (0, 1 or 2) present in the individuals. The algorithm was implemented using the SOM toolbox developed for Matlab (The Mathworks 2001) by the Laboratory of Information and Computer Science in the Helsinki University of Technology (Alhoniemi et al., 2000). Initialization methods and the choice of the grid were based on the suggestions of these authors.

(iii) Complementary approaches

(a) FCA

FCA was performed to characterize genetic variation of both individuals and populations through the GENETIX software (V4.05.2, 2004; Belkhir et al., 1996).

(b) The AS method

AS distances between individuals were calculated at each locus and then averaged over loci (SanCristobal et al., 2006). In order to get sufficient precision, analyses were restricted to a subset of 2522 individuals that shared at least ten typed loci with all the others. Using the AS distance, individuals were submitted to UPGMA clustering (Sneath & Snokal, 1973) calculated with the ‘hclust’ method of the S-plus software suite (Becker et al., 1988). The resulting 12 groups (additional Fig. S1 of SanCristobal et al., 2006) were further analysed along the same rationale.

(c) STRUCTURE (St)

Data were analysed using the STRUCTURE software (Pritchard, Wen, Falush, Version 2.2, April 2007), under the admixture model. Classification was performed assuming several numbers of clusters, mainly from 8 to 12.

(d) NJ tree

The matrix of Reynolds genetic distances (Reynolds et al., 1983) was derived and summarized graphically in an NJ tree (Saitou & Nei, 1987). Following the results given in Fig. 3 of SanCristobal et al. (2006), only significant clusters of populations are reported here. They correspond to the nodes of the tree that are repeatedly found in bootstrap resampling of markers (bootstrap values higher than 75%).

(e) PCA

PCA was performed on the different populations and breeds, based on the allele frequencies in populations at the 50 markers. Missing values were replaced by the mean values of frequencies in the whole data set. Calculations were done using the ‘prcomp’ method of S-Plus, and results were visualized with the Tetralogie software (Dkaki and Dousset, http://atlas.irit.fr/; Dousset, 2003), which allows the user to have a global four-dimensional view of results and to select interesting points of view.

3. Results

(i) Classification of individuals and populations with SOM

Several prior runs were performed using the complete data set, with different sizes of the output layer. A hexagonal grid of 10×20 cells was chosen that allowed the topographic error to get an acceptable value. At the end of the learning process, each individual was assigned to a single cell in the SOM map. The quality of this assignment is characterized by the topographic error rate, which was found to be lower than 0·05, indicating that the assignment of an individual at some location in the SOM map was robust.

The map was further classified into eight clusters, using Euclidean distance and Ward's linkage method (Fig. 1). Similarities between the clusters are characterized by the resulting tree (Fig. 1 a, b). The results of the ‘U-matrix’ algorithm are shown Fig. 1 c. They indicate the limits between clusters with dark points. The darker the limit is, the stronger the differentiation between the clusters is. For example, the 6th cluster (corresponding to the Chinese Meishan breed) is strongly separated from the other ones. This means that although this cluster lies in the middle of the map, it must be considered as very distant from its neighbours. Hence, analysing proximities on the SOM map must take into account these limits.

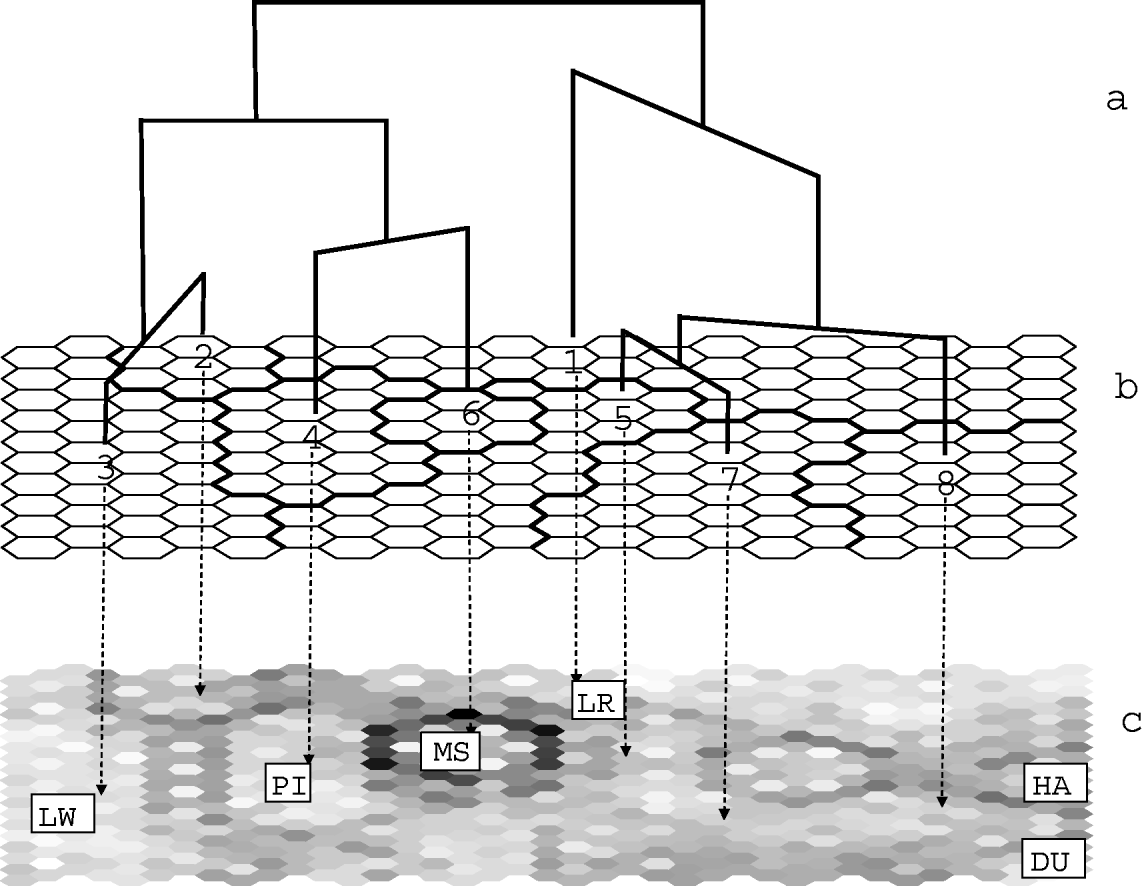
Fig. 1. Classification of European pigs generated by SOM. (a) SOM tree of the eight clusters defined in Table 1. (b) Classification of pig populations on the SOM map. The contents of the eight SOM clusters are detailed in Table 1. The repartition of the breeds on this map is shown in Figure 2. (c) U-matrix map. This map is made up of ‘mini-cells’ corresponding to both the output neurones and to the links between adjacent cells. Black or dark mini-cells indicate links between unrelated or distant cells and hence limits between clusters. The main breeds corresponding to clusters are Landrace LR, Large White LW, Pietrain PI for clusters 1, 3 and 4, respectively, Meishan for cluster 6 and Duroc and Hampshire for cluster 8.

Table 1 gives the list of populations that are representative of each cluster, with the proportion of individuals of the population that were found in the cluster. In general, most individuals from the same population were assigned within a single cluster. However, most clusters included also a small number of individuals from other populations. Individuals from different populations of the same breed (Large White, Landrace, Meishan, Duroc and Hampshire) were generally assigned to a single cluster, with some exceptions. Three populations from the cosmopolitan breeds, and three local breeds were split into two SOM clusters: the Icelandic Landrace (ISLR09) split into clusters 3 and 1; the 1970 sample of the Danish Landrace (DKLR05) split into clusters 1 and 5; the German Hampshire line (DEHA02) split into clusters 8 and 1, the Spanish Negro Canario (NC) and the Italian Casertana (CT) breeds. A few populations and breeds were spread over three or four clusters: the Italian Nera Siciliana (NS), the French Créole (CR) and the synthetic DRB (DR).

Table 1. Distribution of pig populations in the different clusters (1–8) given by SOM, STRUCTURE (St), AS and NJ methods

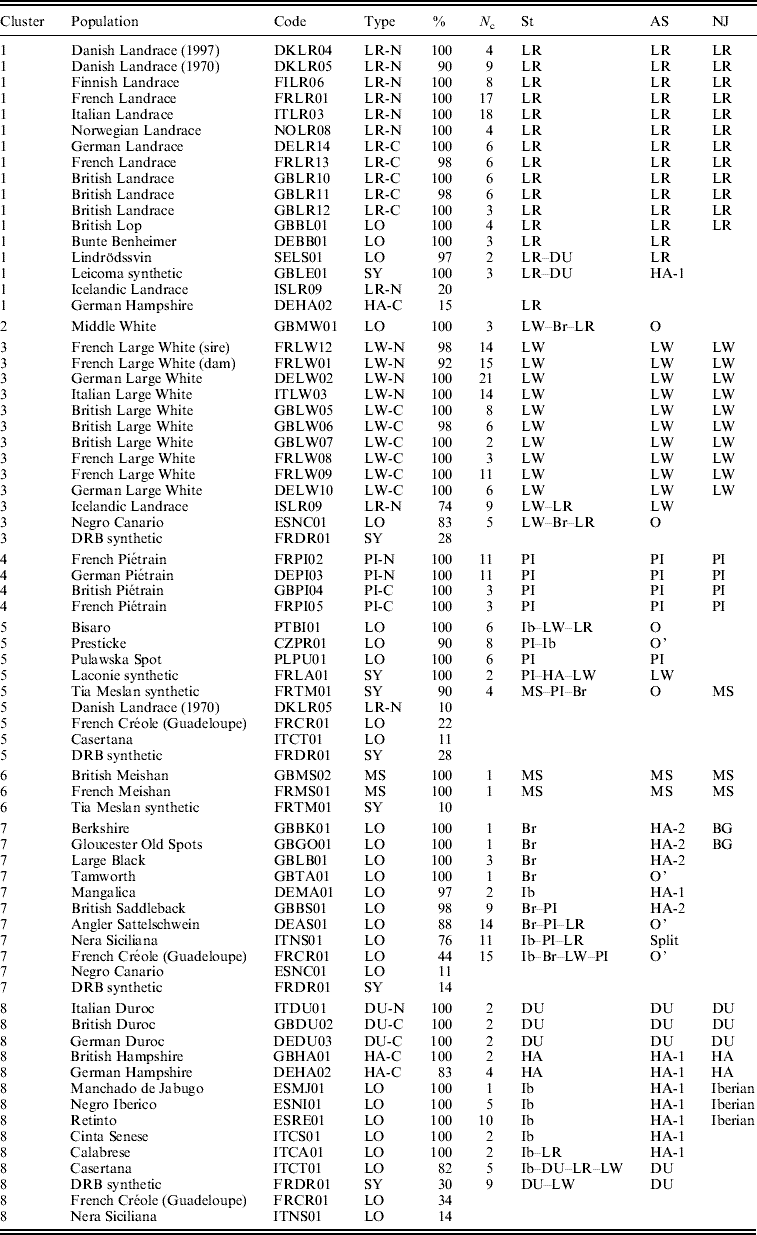
Population: usual names used by the breeders.

Code: concatenation of a two-letter country code, a two-letter breed or line name and a two-digit count. There are a total of 14 countries: CZ=Czech Republic; DE=Germany; DK=Denmark; ES=Spain; FI=Finland; FR=France; GB=the United Kingdom; IS=Iceland; IT=Italy; NO=Norway; PL=Poland; PT=Portugal; SE=Sweden.

Type: LO (local breed), SY (synthetic population), XX-N or XX-C, where XX stands for a cosmopolitan breed (LR, LW, PI, DU or HA), N stands for ‘national line of a cosmopolitan breed’ and C for ‘commercial line’.

%: Percentage of individuals in the population that are assigned to the corresponding SOM cluster (only given if larger than or equal to 10%).

N _c: number of SOM cells harbouring the population.

St, AS and NJ columns: groups and sub-groups identified by these methods (see the text).

The dispersion of individuals on the SOM map is shown in Fig. 2. Populations and breeds whose individuals are assigned to a single SOM cell or to neighbouring cells are shown in Fig. 2 a. The distribution of individuals from synthetic lines and from populations whose individuals are spread in different locations is shown in Fig. 2 b.

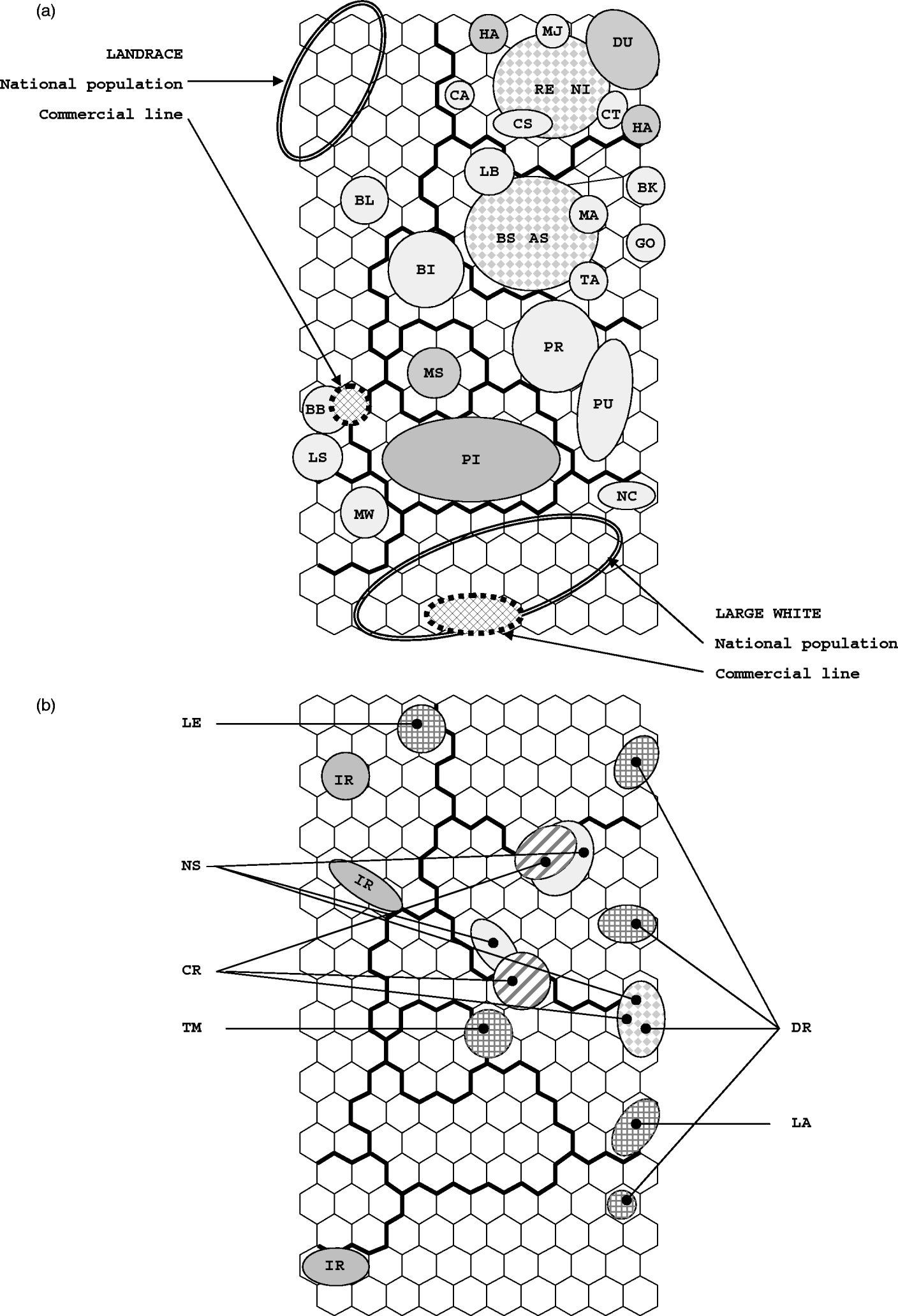
Fig. 2. Repartition on the SOM map of European pig breeds and populations. (a) Repartition on the SOM map of cosmopolitan and local breeds: breeds are designated by their two-letter codes. Examples of the dispersion of individuals from a single national population and from a single commercial line are shown for the Landrace (cluster 1) and the Large White (cluster 3) breeds. The two large dotted circles correspond to pairs of similar breeds that are spread in the same region of the SOM map (RE-NI and AS-BS). (b) Repartition of the four synthetic lines and of populations that are spread in various places on the SOM map. IR stands for the Icelandic Landrace population.

For populations that are not spread in different clusters, we considered the ratio of the number of SOM cells occupied by a population (column N _c, Table 1) to the total number of cells in the cluster. This measure of within-population diversity is plotted against the expected heterozygosity for cosmopolitan breeds (clusters 1, 3 and 4 with 42, 38 and 20 cells, respectively, Fig. 3 a) and for the local breeds (clusters 5, 7 and 8 with 29, 31 and 26 cells, respectively, Fig. 3 b).

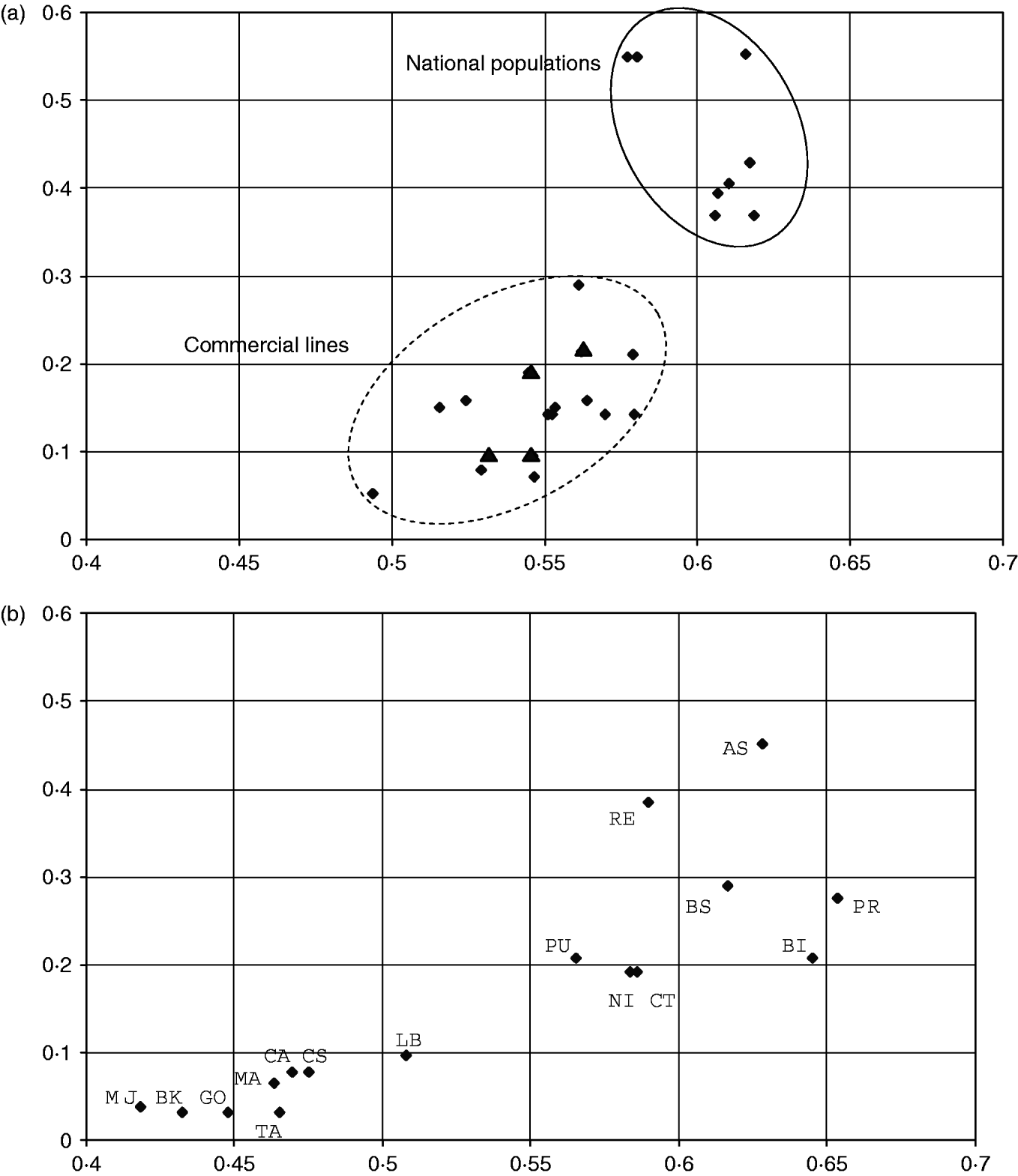
Fig. 3. Relationship between heterozygosity and relative SOM diversity in cosmopolitan and local breeds. Abscissa: expected heterozygosity. Ordinates: relative SOM diversity defined as the ratio of N _c (the number of SOM cells occupied by individuals of the population) to the total number of cells in the corresponding cluster. (a) National populations and commercial lines of cosmopolitan breeds Landrace, Large White and Piétrain (clusters 1, 3 and 4). The Scandinavian Landrace populations (triangles) that show a low heterozygosity behave like the commercial lines. (b) Local breeds (clusters 5, 7 and 8).

(ii) Complementary approaches

(a) AS

Previous results (Fig. S1 of the Supplementary Material section of SanCristobal et al., 2006) are recalled in Table 1. Some populations (BI, MW, NC and TM) were seen as original groups with no link to any other one (denoted with O in Table 1). On the contrary, the two Hampshire populations and a large number of local breeds were seen as a single AS group, roughly corresponding to the 7th and 8th SOM clusters. Reanalysing this group by the AS approach resulted in the identification of four further original populations (PR, AS, CR and TA, denoted by O’ in Table 1) and two sub-groups: ‘HA-1’ made up of nine populations (the two Hampshire lines, three Iberian breeds (NI, MJ and RE), two Italian breeds (CA and CS), the German MA breed and the synthetic LE). The last group ‘HA-2’ included four British breeds (BK, GO, BS and LB).

(b) STRUCTURE

Clustering with STRUCTURE software was repeatedly performed assuming 8–12 clusters, because the large size of the data and these large K numbers of clusters made the algorithm converge to local maxima of the likelihood, whatever the length of the Monte Carlo Markov Chains (MCMC) chains. Several runs were performed with medium chain lengths (5000 or 10 000 for burn-in, followed by 20 000 or 50 000 iterations) to select the best results showing the same distribution of likelihoods. The probability of data increased with K, up to a K value of about 20. Assuming eight clusters allowed five cosmopolitan breeds, the Meishan breed, a group based on Iberian breeds, and a British group of breeds to be identified. The ‘Iberian’ cluster (Ib in Table 1) included the Iberian breeds (NI, MJ and RE), the Italian CS and the German MA. The British cluster (Br in Table 1) was based on British breeds (BK, GO, LB and TA). Individuals from the other breeds were either assigned to a cosmopolitan breed (BL to Landrace and PU to Piétrain), or considered admixed. The corresponding assignments and the make-up of admixed populations are listed in Table 1.

(c) Multivariate analyses

FCA was performed on individuals and on the population means. The first four components accounted for a total of 8·3% of the total inertia on individuals and for a total of 31·5% on populations. For the PCA done on populations’ allele frequencies, the first four components accounted, respectively, for 12, 10·6, 9·7 and 5·7% of the total variance, with a total of 38%. In the following, only results obtained by PCA are shown, due to the high similarities of the result with FCA. Results are shown as two-dimensional projections chosen after the visualization provided by the Tetralogie software (Fig. 4). One component (the second one) allowed the Chinese Meishan breed to be differentiated from all the other populations, with the Tia Meslan synthetic lying between the Meishan and the European breeds (Fig. 4 a). The other three main components allowed four cosmopolitan breeds to be differentiated: large White vs Landrace and Duroc, Landrace vs Duroc and Piétrain vs Duroc (Fig. 4 b).

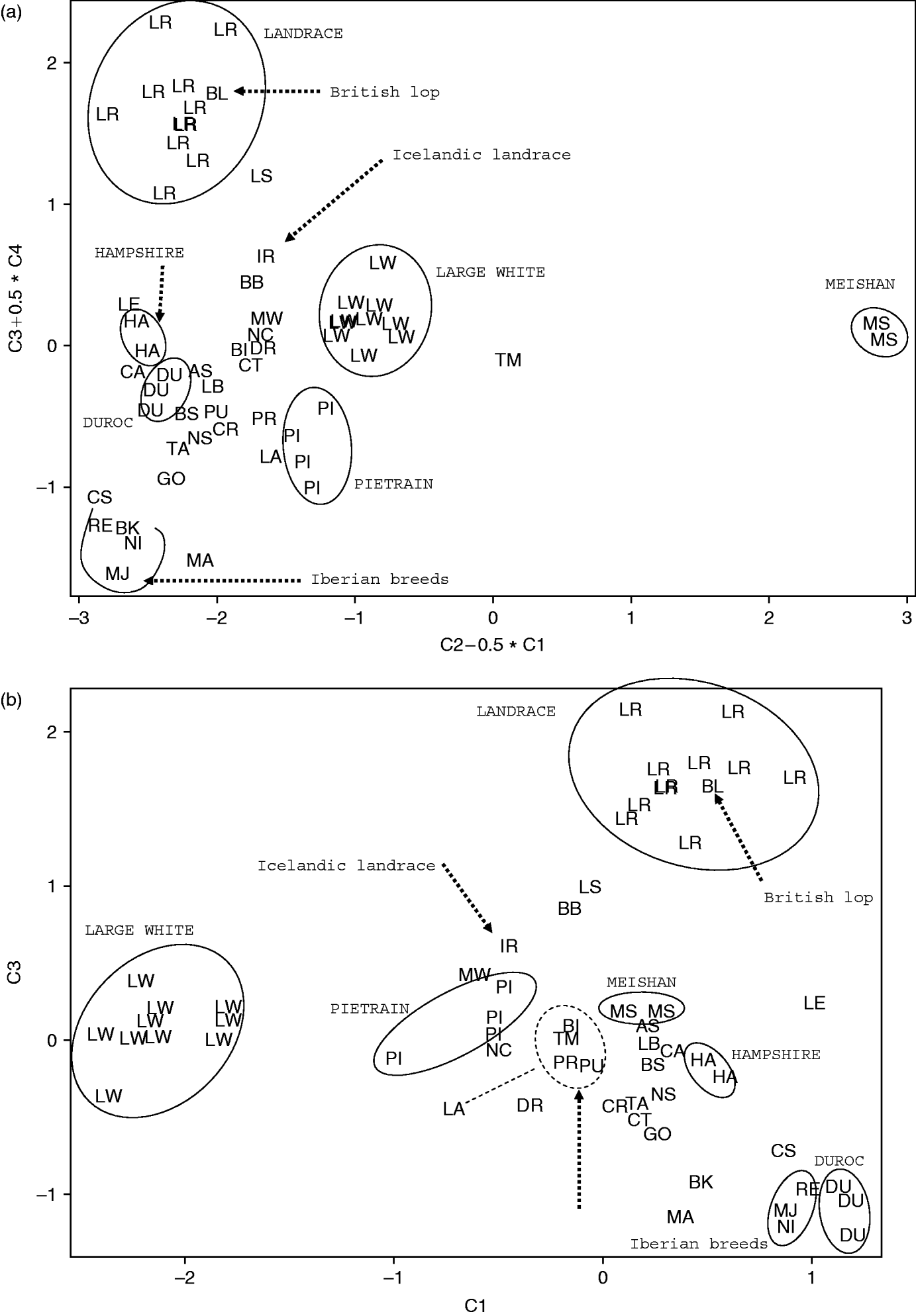
Fig. 4. PCA ordination. Two projections of combinations of the first four components C1, C2, C3 and C4 are shown. Populations are designated by the two-letter code of the breed. IR stands for the Icelandic Landrace population. (a) Coordinates are the combinations C2−C1/2 and C3+C4/2. Note the external position of the Chinese Meishan breed (MS) and of the Tia Meslan synthetic (TM), the intermediate position of the Icelandic Landrace between the Landrace and the Large White clusters, and the position of British Lop inside the Landrace cluster. (b) Coordinates are the combinations C1 and C3. Note the general similarity between this topology and that proposed by SOM (Figs 1 c and 2 a).

(d) Genetic distances

The significant results derived from the NJ classification, based on genetic distances, are recalled in Table 1. In addition to the grouping of populations from the same cosmopolitan breeds, only four significant groupings were found: three Iberian breeds (RE, NI and MJ), two British breeds (BK and GO, denoted by BG in Table 1), the assignment of British Lop (BL) to the Landrace group and the link of the Tia Meslan synthetic to the Chinese Meishan breed (MS).

4. Discussion

We discuss the results obtained in parallel with the different approaches and focus on the added value of the SOM method.

All the methods allowed similar classifications or ordinations of individuals and populations to be proposed. Individuals and populations from the Chinese Meishan breed and from cosmopolitan breeds (Large White, Landrace and Piétrain) were grouped by all methods (SOM, St, AS, NJ and PCA) within their own breed group. Both SOM and AS methods suggested that the Icelandic Landrace population could be partly attached to the Large White and to the Landrace clusters, while the NJ classification did not attach this population to any group. This exception was interpreted as an effect of the stratification within the population (SanCristobal et al., 2006). The other two cosmopolitan breeds (Duroc and Hampshire) and the local breeds were grouped in similar although slightly different ways. Although the AS method clearly identified the Duroc pigs as a separate cluster, while SOM did not, both methods suggested the same groupings (HA-1 and SOM cluster 8, HA-2 and SOM cluster 7). Using STRUCTURE (with eight clusters), the British and the Iberian groups defined by NJ were extended to more breeds, so as to get a classification compatible with SOM and AS clustering. For other populations that were grouped by SOM, STRUCTURE suggested an admixed composition of the corresponding individuals. For example it showed that all the Icelandic pigs are admixed between Landrace and Large White (plus other small contributions). Conversely, for the DEHA02 Hampshire population that was found split by all methods, STRUCTURE strongly indicated that the eight outliers were pure Landrace pigs. This observation, which was confirmed when running a test of assignment (not shown), implies that an error occurred when labelling the DNA samples since Hampshire pigs cannot be confused with Landrace ones. Suggestions of admixture, as given by STRUCTURE, are however dependent on the number K of clusters that are searched for. Increasing K suggested new groupings of populations. For example assuming K=12 resulted in the emergence of a cluster made up of seven populations: five of SOM cluster 5, the British BS and the German AS, which were previously considered as admixed (Table 1). Although this emergence was in accordance with the SOM result and with PCA (Fig. 4 b), the meaning of this cluster was not clear, since it involved two synthetic lines and local breeds from distant European regions. This clustering was not confirmed by AS, for which these populations were seen as original, nor by the first four components of FCA on individuals (not shown). A possible interpretation is that all these individuals were found in the middle of the cloud (as seen in FCA and PCA). Their genotypes might be close to some mean genotype either because these synthetic lines are admixtures from quite different breeds, or because these local breeds would be representative of a common ancestor from which the present cosmopolitan breeds have diverged.

Compared with other unsupervised clustering methods (AS and St), the SOM method provides relationships between clusters (Fig. 1) and a graphical description of data in a finite space (Fig. 2). Similarities between the clusters were characterized by the resulting tree (Fig. 1 a, b). The tree identified two main clades corresponding to the Large White and Landrace cosmopolitan breeds. Considering the positions of the clades on the SOM map (Fig. 1 c), it seemed that the Piétrain was closer to Large White than to Landrace. Similarly, the Hampshire and Duroc breeds were set closer to Landrace than to Large White. Figure 1 c, however, showed that, within cluster 8, the Hampshire breed was separated from its neighbours by a dark fence, corresponding to the large genetic distance between the Hampshire and Duroc breeds. Similarly, the proximity between Piétrain and Meishan (clusters 4 and 6) shown by the tree must be taken with caution since the Meishan is strongly isolated from the other populations (Fig. 1 c). Taking this into account, the dispersion of individuals and breeds on the SOM map provides an interesting global view of the data (Fig. 2).

As reported in other studies (Brosse et al., 2001; Kohonen, 2001; Park et al., 2004) a clear similarity between the topologies given by SOM (Fig. 2 a) and PCA (Fig. 4 b) was found.

The global topology is conserved, but the nonlinear SOM projection introduces two different scales. Large distances between individuals from different clusters are shrunk and represented by distances between clusters. Within a cluster, small distances between similar individuals are expanded, allowing fine structures to be visualized. The large clusters dedicated to Landrace and Large White populations illustrate this. In each one, there were similar populations with small genetic distances (<0·10), but individuals were spread over many SOM cells (42 and 38, respectively). In the other clusters, i.e. clusters 4, 5, 7 and 8, differences in within-population diversity were observed between populations. Individuals from the same population were often found in a single SOM cell, or in neighbouring cells (Fig. 2 a). Several exceptions were observed. Firstly, the samples of the Hampshire breed were found in three non-adjacent regions: one within the Landrace cluster 1 (not shown in Fig. 2 because of probably corresponding to labelling errors of samples), and two within cluster 8. Secondly, two local breeds and one synthetic line were found split into different regions of the SOM map (Fig. 2 b). For cosmopolitan breeds (Landrace, Large White and Piétrain) it was observed that the numbers of cells harbouring animals from the same population were generally smaller for commercial lines (mean values of 5·4, 6 and 3, for the three breeds, respectively), than for national populations (10, 16 and 11, respectively). Examples of this observation were illustrated in Fig. 2 a. Similarly, the larger genetic diversity observed in the NI and RE Iberian breeds compared with MJ was highlighted on the SOM map. It is worth noting that looking at the dispersion of individuals in FCA did not allow such differences to be visualized (not shown). Figure 3 illustrates how populations are differentiated by SOM, according to their diversity. The genetic interpretation of the proposed semi-quantitative measure of diversity is not straightforward. The larger is the heterozygosity, the greater is the increase in this measure, but there is no one-to-one correspondence. Considering cosmopolitan breeds, the distributions of the measure for commercial or national populations did not overlap (except for the national Scandinavian populations with low diversity), whereas the distributions of heterozygosity did (Fig. 3 a). Figure 3 b suggested that there are two types of local breeds: a first group showed a low diversity smaller than that observed in specialized commercial lines, whereas the second group seemed to be made of potentially ‘healthy’ breeds with high indices of diversity. As for the national populations of cosmopolitan breeds, there was no clear relationship between this SOM measure of diversity and expected heterozygosity.

The dispersion of individuals on the SOM map in proportion to the internal diversity of their population (as reflected for national versus commercial lines, or for the three Iberian breeds) did not prevent them from being clustered. The extension of the BK–GO cluster (NJ) to a larger set of British breeds, and the Iberian group (NI–RE–MJ) to some Italian breeds (in SOM clusters 7 and 8), was validated by the STRUCTURE analysis but did not correspond to any significant cluster with NJ. Even for populations from the Landrace breed, the bootstrap value was quite low (85%, Fig. 3 of SanCristobal et al., 2006). One explanation may be the sensitivity of the NJ algorithm to large branch lengths: breeds with low heterozygosity could not be clustered, because strong genetic drift in such populations generated large genetic distances with other populations. This effect is clearly seen with the Iberian breeds, for which the bootstrap value was reduced from 93% to 75% when adding the MJ inbred breed to the pair RE–NI. This ability to cluster individuals from populations exhibiting very different internal variability may be an interesting feature of the method. Such an efficiency of ANNs in classification problems has been reported by Guinand et al. (2002), showing that ANNs can outperform likelihood-based methods for assigning individuals to their population of origin, especially when working on empirical rather than on simulated data.

The different methods pointed to populations that seemed heterogeneous. Except for the DEHA02 case, which is probably due to some labelling error, four cases were identified with three or four SOM locations: the Créole (CR) and Nera Siciliana (NS) local breeds, the Icelandic Landrace population (denoted as IR in Figs 2 b and 4) and the synthetic DRB (DR). For the other three synthetic breeds (LA, LE and TM), a single SOM region was found in a location between the components of the admixture predicted by STRUCTURE. For the Icelandic Landrace the SOM localizations of its components were in agreement with the composition given by STRUCTURE. However, it was not the case for CR, NS and DR (Fig. 2 b). This may suggest that splitting of a population on the SOM map may be indicative of admixture, but the reverse is not true. It may also be noted that the common SOM sub-localizations of the Créole and the Nera Siciliana breeds corresponded to the second lowest genetic distance between different breeds (after the very similar NI and RE Iberian breeds). There may be also a relationship with genetic structure since the dispersion of Créole, Nera Siciliana and Icelandic Landrace breeds was associated with significant departures from the Hardy–Weinberg equilibrium (F_IS=0·10, 0·06 and 0·05, respectively; SanCristobal et al., 2006) and large expected heterozygosities. However, this is not a systematic link: the synthetic DRB did not show any departure from the Hardy–Weinberg equilibrium (F_IS=0·01) while it is spread over four SOM regions.

5. Conclusion

Introducing Kohonen's SOM method to analyse a large genetic data set contributed several improvements to help apprehend a complex structure. It provided a global view on the data without any prior hypothesis on their organization. Using a finite space to describe the data made it possible to get a look at many individual data; about 2700 items being spread here over 200 hexagonal cells. The reduced dimensionality of the space implies nonlinearity and, hence, changes in the global topology. Accounting for such distortions is made possible with specific tools (hierarchical clustering, U-matrix visualization of limits between sub-regions) that allow local topology among similar entities to be recovered. In the present genetic context the nonlinear projection provided useful information on the organization of diversity, firstly by clustering individuals that share a global similarity (pertaining to the same cosmopolitan breed, or to a group of British breeds, in our example), then by spreading individuals from such a cluster without overlap between clusters. This allowed similar populations to be clustered in spite of their large genetic distances due to genetic drift. This is an interesting feature of the method when large samples from populations with different histories are considered. This seems to be a significant advantage compared with FCA that generally develops overlapping clouds of points. The dispersion of populations on the map, as well as intermediate locations of individuals, may be an index of admixture, or of sub-structuring. As a model-free approach, it may be valuable in combination with an approach like STRUCTURE, for which choosing the right number of clusters may be difficult with complex and large data sets. An empirical measure of diversity, the proportion of SOM cells occupied by one population in its cluster, was proposed. This measure seemed to be roughly independent of expected heterozygosity and to have some discriminatory power, even if its genetic meaning remains to be understood.

The method may help in raising genetic or evolutionary questions, since it points to features that might remain invisible while using model-driven tools. For example in the case of genetic diversity, a single analysis pointed to several aspects: similarity and relationships between breeds, variations of within-population diversity, suggestion of admixture, discrimination between groups of populations. Even if it does not allow any specific genetic hypothesis to be tested, the method is a valuable descriptive tool to get a comprehensive view on the data and to participate in the discussion of the results given by various specific models.